„Részecskefizika” változatai közötti eltérés
(Új oldal, tartalma: „*Előfeltételek: :: # Relativisztikus kinematika :: # Kvantummechanika (Dirac-egyenlet) :: # Csoportelmélet (csoport irreducibilis ábrázolása) :: # SU2, izospin, szim…”) |
|||
| 1. sor: | 1. sor: | ||
*Előfeltételek: | *Előfeltételek: | ||
| − | :: # Relativisztikus kinematika | + | ::# Relativisztikus kinematika |
| − | :: # Kvantummechanika (Dirac-egyenlet) | + | ::# Kvantummechanika (Dirac-egyenlet) |
| − | :: # Csoportelmélet (csoport irreducibilis ábrázolása) | + | ::# Csoportelmélet (csoport irreducibilis ábrázolása) |
| − | :: # SU2, izospin, szimmetriák... | + | ::# SU2, izospin, szimmetriák... |
==Ajánlott irodalom== | ==Ajánlott irodalom== | ||
| 17. sor: | 17. sor: | ||
==Tematika== | ==Tematika== | ||
| − | + | 1. [[Elemi részecskék és kölcsönhatásaik]] | |
::-Részecskeosztályozás és kölcsönhatások | ::-Részecskeosztályozás és kölcsönhatások | ||
::-Megmaradó mennyiségek | ::-Megmaradó mennyiségek | ||
::-Hadronok kvarkmodelljének alapjai | ::-Hadronok kvarkmodelljének alapjai | ||
| − | + | 2. A kvantumtérelmélet alapjai (a II. kvantálás) | |
::-Szabad skalármező kanonikus kvantálása (propagátor, Wich-tétel) | ::-Szabad skalármező kanonikus kvantálása (propagátor, Wich-tétel) | ||
::-Megmaradó mennyiségek, Noether-tétel | ::-Megmaradó mennyiségek, Noether-tétel | ||
::-Elektromágneses mező kovariáns kvantálása (fermionok kvantálása - elektron, pozitron) | ::-Elektromágneses mező kovariáns kvantálása (fermionok kvantálása - elektron, pozitron) | ||
| − | + | 3. Relativisztikus kvantumelektrodinamika alapjai, Feynman gráfok | |
::-<math>e^{-}e^{-} \rightarrow e^{-}e^{-}</math> rugalmas szórás | ::-<math>e^{-}e^{-} \rightarrow e^{-}e^{-}</math> rugalmas szórás | ||
::-<math>e^{+}e^{-}</math> annihiláció | ::-<math>e^{+}e^{-}</math> annihiláció | ||
| 41. sor: | 41. sor: | ||
-Modern detektorok és gyorsítók részletes felépítése | -Modern detektorok és gyorsítók részletes felépítése | ||
| + | |||
| + | [[Kategória:Részecskefizika]] | ||
| + | [[Kategória:MSc]] | ||
A lap jelenlegi, 2009. szeptember 15., 07:10-kori változata
- Előfeltételek:
- Relativisztikus kinematika
- Kvantummechanika (Dirac-egyenlet)
- Csoportelmélet (csoport irreducibilis ábrázolása)
- SU2, izospin, szimmetriák...
Ajánlott irodalom
-Patkós András-Polónyi János: Sugárzás és részecskék
-Haykron-Zuker: Kvantumtérelmélet
-Perkins: Bevezetés a nagyenergiájú fizikába
-David C. Cheng: Elementary particle physics
-O. Nachtmann: Kísérleti fizika
Tematika
1. Elemi részecskék és kölcsönhatásaik
- -Részecskeosztályozás és kölcsönhatások
- -Megmaradó mennyiségek
- -Hadronok kvarkmodelljének alapjai
2. A kvantumtérelmélet alapjai (a II. kvantálás)
- -Szabad skalármező kanonikus kvantálása (propagátor, Wich-tétel)
- -Megmaradó mennyiségek, Noether-tétel
- -Elektromágneses mező kovariáns kvantálása (fermionok kvantálása - elektron, pozitron)
3. Relativisztikus kvantumelektrodinamika alapjai, Feynman gráfok
- -
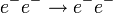 rugalmas szórás
rugalmas szórás - -
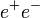 annihiláció
annihiláció - -eN (elektron-nukleon) mélyen rugalmas szórás
- -
Amiről a jelen kurzuson NEM lesz szó (előbb-utóbb azért ide kerül):
-Renormálás
-Perturbációszámítás magasabb rendjei
-Kvantumtérelmélet funkcionálintegrálos megfogalmazása
-Modern detektorok és gyorsítók részletes felépítése