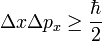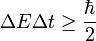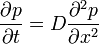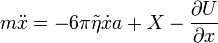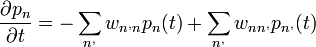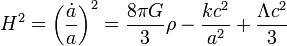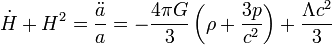„Képlettár” változatai közötti eltérés
Naxa (vitalap | szerkesztései) a |
|||
| (8 közbenső módosítás ugyanattól a szerkesztőtől nincs mutatva) | |||
| 1. sor: | 1. sor: | ||
| − | + | Megj. Lent minden fejezetcím egyben link is, amely mögött gyakran tételhez mutató linket találtok (amik nincsenek ezen a lapon felsorolva). | |
| − | + | =[[Newton II]]= | |
| − | + | {{:Newton II}} | |
| − | + | =[[Gravitációs törvény]]= | |
| − | + | {{:Gravitációs törvény}} | |
| − | + | =[[Erők gyorsuló koordináta rendszerben]]= | |
| − | + | {{:Erők gyorsuló koordináta rendszerben}} | |
| − | + | =t és x [[Lorentz transzformáció]]ja= | |
| − | + | {{:Lorentz transzformáció}} | |
| − | + | ||
| − | + | =[[Tömeghéj feltétel]]= | |
| − | + | {{:Tömeghéj feltétel}} | |
| − | + | =[[Kanonikus egyenletek]]= | |
| − | + | {{:Kanonikus egyenletek}} | |
| − | + | =[[Harmonikus oszcillátor energiája, Hamilton operátora]]= | |
| − | + | {{:Harmonikus oszcillátor energiája, Hamilton operátora}} | |
| − | + | =[[Léptető operátorok]]= | |
| − | + | {{:Léptető operátorok}} | |
| − | + | =[[Doppler effektus]]= | |
| − | + | {{:Doppler effektus}} | |
| − | + | =[[Archimedes törvénye]]= | |
| − | + | {{:Archimedes törvénye}} | |
| − | + | =[[Bernoulli egyenlet]]= | |
| − | + | {{:Bernoulli egyenlet}} | |
| − | + | =[[Euler egyenlet]]= | |
| − | + | {{:Euler egyenlet}} | |
| − | + | =[[Navier-Stokes]]= | |
| − | + | {{:Navier-Stokes}} | |
| − | + | =[[Termodinamika főtételei]]= | |
| − | + | {{:Termodinamika főtételei}} | |
| − | + | =[[Ideális gáz, Van der Waals gáz állapotegyenlete]]= | |
| − | + | {{:Ideális gáz, Van der Waals gáz állapotegyenlete}} | |
| − | + | =[[Fundamentális egyenlet]]= | |
| − | + | {{:Fundamentális egyenlet}} | |
| − | + | =[[Euler összefüggés]]= | |
| − | + | {{:Euler összefüggés}} | |
| − | + | =[[Gibbs-Duhem reláció]]= | |
| − | + | {{:Gibbs-Duhem reláció}} | |
| − | + | =[[Maxwell-egyenletek]] (integrális, differenciális)= | |
| − | + | {{:Maxwell-egyenletek}} | |
| + | |||
| + | =[[Ponttöltés, dipól potenciálja]]= | ||
| + | {{:Ponttöltés, dipól potenciálja}} | ||
| + | =[[Coulomb törvény]]= | ||
| + | {{:Coulomb törvény}} | ||
| + | =[[D-E összefüggése]]= | ||
| + | {{:D-E összefüggése}} | ||
| + | =[[B-H összefüggése]]= | ||
| + | {{:B-H összefüggése}} | ||
| + | =[[Biot-Savart törvény]]= | ||
| + | {{:Biot-Savart törvény}} | ||
| + | =[[Lorentz-erő]]= | ||
| + | {{:Lorentz-erő}} | ||
| + | =[[Kontinuitási egyenlet]] (j-re, m-re)= | ||
| + | {{:Kontinuitási egyenlet}} | ||
| + | |||
| + | =[[Hullám egyenlet]]= | ||
| + | {{:Hullám egyenlet}} | ||
| + | =[[Snellius-Descartes törvény]]= | ||
| + | {{:Snellius-Descartes törvény}} | ||
| + | =[[Eikonál egyenlet]]= | ||
| + | {{:Eikonál egyenlet}} | ||
| + | =[[Leképezési törvény]]= | ||
| + | {{:Leképezési törvény}} | ||
| + | =[[Schrödinger egyenlet]] (időfüggő, időfüggetlen)= | ||
| + | {{:Schrödinger egyenlet}} | ||
| + | =[[Határozatlansági reláció]]k= | ||
| + | {{:Határozatlansági reláció}} | ||
| + | |||
| + | =[[Pauli egyenlet]]= | ||
| + | {{:Pauli egyenlet}} | ||
| + | =[[Félempirikus kötési formula]]= | ||
| + | {{:Félempirikus kötési formula}} | ||
| + | =[[Curie-Weiss törvény]]= | ||
| + | {{:Curie-Weiss törvény}} | ||
| + | =[[Bragg egyenlet]]= | ||
| + | {{:Bragg egyenlet}} | ||
| + | =[[Diffúziós egyenlet]]= | ||
| + | {{:Diffúziós egyenlet}} | ||
| + | =[[Langevin egyenlet]]= | ||
| + | {{:Langevin egyenlet}} | ||
| + | =[[Master egyenlet]]= | ||
| + | {{:Master egyenlet}} | ||
| + | =[[Friedmann egyenletek]]= | ||
| + | {{:Friedmann egyenletek}} | ||
A lap jelenlegi, 2012. június 9., 12:00-kori változata
Megj. Lent minden fejezetcím egyben link is, amely mögött gyakran tételhez mutató linket találtok (amik nincsenek ezen a lapon felsorolva).
Tartalomjegyzék
- 1 Newton II
- 2 Gravitációs törvény
- 3 Erők gyorsuló koordináta rendszerben
- 4 t és x Lorentz transzformációja
- 5 Tömeghéj feltétel
- 6 Kanonikus egyenletek
- 7 Harmonikus oszcillátor energiája, Hamilton operátora
- 8 Léptető operátorok
- 9 Doppler effektus
- 10 Archimedes törvénye
- 11 Bernoulli egyenlet
- 12 Euler egyenlet
- 13 Navier-Stokes
- 14 Termodinamika főtételei
- 15 Ideális gáz, Van der Waals gáz állapotegyenlete
- 16 Fundamentális egyenlet
- 17 Euler összefüggés
- 18 Gibbs-Duhem reláció
- 19 Maxwell-egyenletek (integrális, differenciális)
- 20 Ponttöltés, dipól potenciálja
- 21 Coulomb törvény
- 22 D-E összefüggése
- 23 B-H összefüggése
- 24 Biot-Savart törvény
- 25 Lorentz-erő
- 26 Kontinuitási egyenlet (j-re, m-re)
- 27 Hullám egyenlet
- 28 Snellius-Descartes törvény
- 29 Eikonál egyenlet
- 30 Leképezési törvény
- 31 Schrödinger egyenlet (időfüggő, időfüggetlen)
- 32 Határozatlansági relációk
- 33 Pauli egyenlet
- 34 Félempirikus kötési formula
- 35 Curie-Weiss törvény
- 36 Bragg egyenlet
- 37 Diffúziós egyenlet
- 38 Langevin egyenlet
- 39 Master egyenlet
- 40 Friedmann egyenletek
Newton II
Gravitációs törvény
Erők gyorsuló koordináta rendszerben
Az első korrekciós tag az egyenes gyorsulásnál is fellépett transzlációs tag, a második a centrifugális erő, a harmadik a Coriolis-erő, a negyedik az Euler-erő.
t és x Lorentz transzformációja
Tömeghéj feltétel
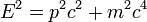
Kanonikus egyenletek
Harmonikus oszcillátor energiája, Hamilton operátora
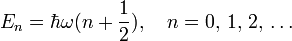
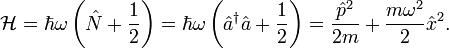
Léptető operátorok
Doppler effektus
mozgó forrás:
mozgó észlelő:
Archimedes törvénye
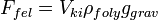
Bernoulli egyenlet
Euler egyenlet
Az Euler-egyenlet az ideális folyadék mozgásegyenlete:
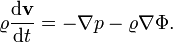
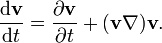
Termodinamika főtételei
Ideális gáz, Van der Waals gáz állapotegyenlete
Bővebben: Egyesített gáztörvény
Bővebben: Fenomenologikus termodinamika#Van der Waals gázok
Fundamentális egyenlet
Euler összefüggés
Ha 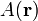 homogén függvény, azaz
homogén függvény, azaz
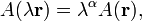
ahol 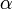 a homogenitási fok, akkor
a homogenitási fok, akkor
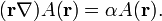
A termodinamikában 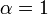 általában, például az
általában, például az 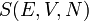 függvénynél.
függvénynél.
Gibbs-Duhem reláció
Maxwell-egyenletek (integrális, differenciális)
Az egyenletek összegzése
Maxwell négy egyenlete a következőket írja le,
- 1. Az elektromos tér forrásos, azaz elektromos töltés jelenlétében erővonalak indulnak a pozitív töltésekről, melyek a negatív töltéseken végződnek. (Gauss-törvény)
- 2. A mágneses indukció változása elektromos teret indukál, melynek iránya ellenkező mint az őt létrehozó változás. (A Lenz-törvény és Faraday indukciós törvényének egyesítése)
- 3. A mágneses tér forrásmentes, azaz a mágneses tér erővonalai önmagukba záródnak. (Gauss mágneses törvénye),
- 4. Az elektromos áram, illetve a folytonossági egyenlet kielégítéséből adódó eltolási áram mágneses teret hoz létre. (Ampère-törvény)
A makroszkopikus egyenletek SI mértékegységrendszerben:
| Megnevezés | Sorszám | Differenciális alak | Integrális alak |
|---|---|---|---|
| Gauss-törvény | I. | 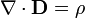
|
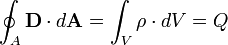
|
| Faraday-Lenz-törvény | II. | 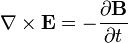
|
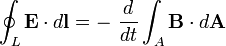
|
| Gauss mágneses törvénye |
III. | 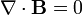
|
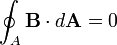
|
| Ampère-törvény |
IV. | 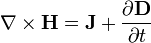
|
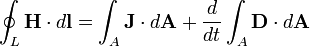
|
| Jelölés | Név | SI mértékegység |
|---|---|---|
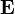
|
elektromos térerősség | volt per méter: 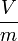
|
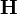
|
mágneses térerősség | amper per méter: 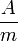
|
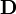
|
elektromos indukció | amperszekundum per négyzetméter: 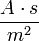
|
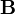
|
mágneses indukció | Voltszekundum per négyzetméter vagy tesla: 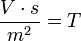
|
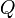
|
elektromos töltés | amperszekundum vagy coulomb: 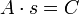
|
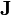
|
áramsűrűség | amper per négyzetméter: 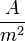
|
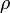
|
elektromos töltéssűrűség | coulomb per köbméter: 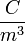
|
Ponttöltés, dipól potenciálja
Ponttöltés potenciálja:
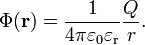
Dipól potenciálja:
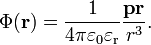
Coulomb törvény
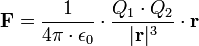 .
.
D-E összefüggése
B-H összefüggése
Biot-Savart törvény
Lorentz-erő
![\mathbf{F}=q[\mathbf{E}+(\mathbf{v}\times\mathbf{B})]](/images/math/b/5/a/b5a66bbfb93e22f6f60240a135dda69f.png)
Kontinuitási egyenlet (j-re, m-re)
Hullám egyenlet
Snellius-Descartes törvény
Eikonál egyenlet
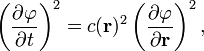
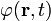 az eikonál.
az eikonál.
Leképezési törvény
Schrödinger egyenlet (időfüggő, időfüggetlen)
általában
spec eset: nem függ az időtől
Határozatlansági relációk
Általánosan
Néhány fontosabb spec. eset:
Pauli egyenlet
![\left \{ \frac{1}{2m}\left[\boldsymbol{\hat{\sigma}} \cdot (\mathbf{\hat{p}}-Q\mathbf{A})\right]^2 + Q\Phi \right \} \boldsymbol{\Psi} = i \hbar \frac{\partial}{\partial t} \boldsymbol{\Psi}.](/images/math/9/f/4/9f48481b4e8a665082b1d46b0546047f.png)
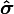 a Pauli-mátrixokból képzett vektor;
a Pauli-mátrixokból képzett vektor;
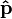 az impulzus;
az impulzus;
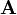 a vektorpotenciál;
a vektorpotenciál;
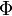 a skalárpotenciál;
a skalárpotenciál;
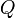 a részecske töltése,
a részecske töltése, 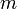 a tömege.
a tömege.
A Pauli-mátrixok a kételemű hullámfüggvényspinor elemeire hatnak.
Félempirikus kötési formula
A kötési energia:
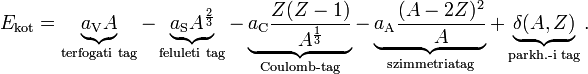
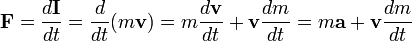
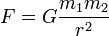
![F - ma_0 -m\left[ \omega \times \left( \omega \times R \right)\right] - 2m\left( \omega \times v^{\prime}\right) - m\left( \frac{d \omega}{dt} \times R\right) = ma^{\prime}](/images/math/f/4/c/f4cdbc4b1c2d6030d0accf0bed1c27bb.png)
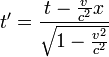
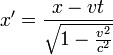
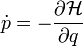
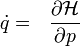
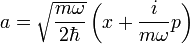
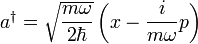
![[a,a^\dagger]=1\,](/images/math/c/a/2/ca294b5fddde3b091c8a4ccbf89992b1.png)
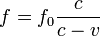
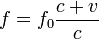
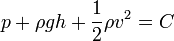
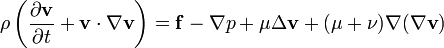
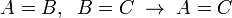
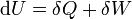
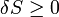
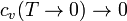
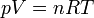
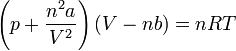
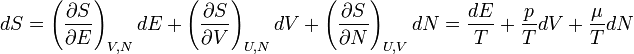
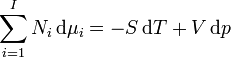
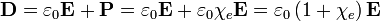
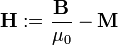
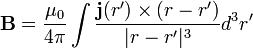
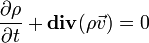
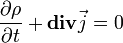
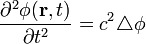
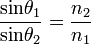
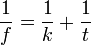
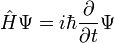
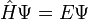
![\Delta O_1 \Delta O_2 \geq \frac{1}{2}|\overline{[\mathbf{O}_1,\mathbf{O}_2]}|](/images/math/d/8/a/d8a20f6e79a0d9790aec79b985b2cead.png)