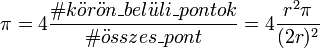A statisztikus fizikai szimulációk alapjai és a Monte Carlo módszer '12
Tartalomjegyzék
Statisztikus fizikai szimulációk alapjai
Legyen egy sokaságunk, aminek az energiája 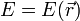 , ahol
, ahol 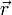 az összes szabadsái fokot tartalmazza (mechanikai rendszerre
az összes szabadsái fokot tartalmazza (mechanikai rendszerre 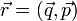 ). Ha a rendszer követi a Boltzmann-statisztikát, akkor a rendszer
). Ha a rendszer követi a Boltzmann-statisztikát, akkor a rendszer ![[\vec{r}, \vec{r}+d \vec{r}]](/images/math/5/6/1/56187ee1de8ce46a085984701d48d250.png) intervallumban való megtalálási valószínűsége:
intervallumban való megtalálási valószínűsége:
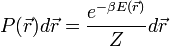
Egy A mennyiség átlagát a sokaságon a következőképp számoljuk (PS = phase space = fázistér):
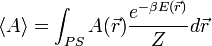
Az integrált csak akkor tudjuk egzaktul kiszámolni, ha a fázistér minden pontjára kiértékeljük a függvényt, és úgy átlagolunk. A Monte-Carlo integrálással ezt a problémát oldhatjuk meg. Az 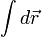 helyére
helyére 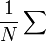 írunk, így egy véges összeget kell elvégeznünk. A pontok számát (N) az határozza meg, hogy mekkora pontossággal akarjuk az integrált meghatározni. Az integrál dimenziójától függetlenül a hiba
írunk, így egy véges összeget kell elvégeznünk. A pontok számát (N) az határozza meg, hogy mekkora pontossággal akarjuk az integrált meghatározni. Az integrál dimenziójától függetlenül a hiba 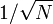 szerint csökken, vagyis 10x nagyobb pontossághoz 100x annyi pontot kell kiszámolni.
szerint csökken, vagyis 10x nagyobb pontossághoz 100x annyi pontot kell kiszámolni.
Molekuladinamika
A molekuladinamika a részecskék mikroszkopikus dinamikájának követésével foglalkozik. Valódi rendszerben 1023 nagyságrendű részecske van, ezt a mai számítógépekkel szimulálni lehetetlen. Azonban ennél kevesebb részecskét is elég szimulálnunk ahhoz, hogy a termodinamikai tulajdonságokat vizsgálhassuk. A szimulációkban a párkölcsönhatásokat vesszük figyelembe, ám lehetséges közelítéseket tenni. A részecskék közt a Van der Waals erő hat, ami elég gyorsan lecseng, így távoli részecskék közt elhanyagolható (ezen a pontot különbözik a molekuladinamika és a gravitációs N-test szimuláció, ahol az 1/r2-es erő miatt nem hanyagolható el a kölcsönhatás).
A szimulációban van tehát N darab részecske, melyekre a Newton-törvények alapján kiszámítjuk a rájuk ható erőt, majd léptetjük a rendszert. Mivel a kezdőállapotokat általában nem a termodinamikai egyensúlyból indítjuk, meg kell várni, hogy a rendszer beálljon abba. Hogy mikor állt be, azt az ekvipartíció segítségével mutathatjuk ki:
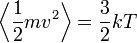
Ha a rendszer elérte az egyensúlyi állapotát, mérhetővé válnak a termodinamikai változók (hőmérséklet, nyomás, hőkapacitás, stb.)
Fizikai mennyiségek mérése a szimulációkban
Pillanatnyi hőmérséklet
Bár azt mondtuk, hogy a rendszert az egyensúlyi állapotában vizsgáljuk, a nem egyensúlyi állapotban is bevezethetünk egy pillanatnyi hőmérsékletnek nevezett mennyiséget. Termikus egyensúlyban igaz az ekvipartíció:
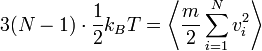 ,
,
ahol 3(N-1) a szabadsági fokok száma (a TKP 3 koordinátája van levonva). A nem egyensúlyi helyzetben, bár nem igaz az ekvipartíció, ezt a képletet alkalmazhatjuk a hőmérséklet meghatározására.
Teljes energia
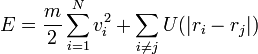
Hőkapacitás
Fluktuáció-disszipáció tétel alapján:
![C_V = \frac{1}{k_BT^2}[\langle E^2 \rangle - \langle E \rangle^2]](/images/math/5/6/6/5665d1b98f0b1a2a48c050809050fe1e.png)
Nyomás
A nyomást a viriál-tétel segítségével fejezhetjük ki:
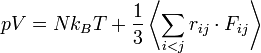
Verlet-algoritmus
Molekuladinamikai szimulációkban legtöbbször a Verlet-algoritmust használják a diffegyenletek megoldására. A Runge-Kuttával szemben több előnye van:
- gyorsabb, mert egy lépésben csak egyszer kell a gyorsulásokat számolni
- majdnem olyan pontos, mint a RK4 (
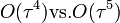 )
) - jól megőrzi az energiát
- időtükrözésre nem változik (ez a részleges egyensúly feltétele miatt fontos)
A Verlet-algoritmus egy lépése (R(t) a koordináták, V(t) a sebességek, A(t) a gyorsulások):
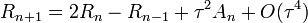
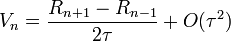
Hátrányai:
- két előző lépést használ, így nem indítható 1 kezdeti feltételből
- a sebesség és a pozíció nem egyszerre frissítődik, a sebesség "le van maradva"
Megoldás: velocity-Verlet algoritmus:
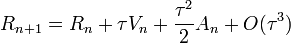
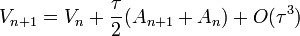
- R-ben már csak
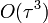 pontosságú
pontosságú - ez már nem 2 előző lépést használ
- koordináták és sebességek egyszerre frissülnek
- sebesség is
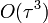 pontosságú
pontosságú
Gravitációs N-test szimuláció
Gravitációs N-test szimulációkor, a kölcsönhatásnak az említett 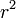 -es lecsengése miatt, nem lehet eltekinteni a hosszútávú kölcsönhatásoktól.
-es lecsengése miatt, nem lehet eltekinteni a hosszútávú kölcsönhatásoktól.
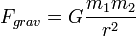
A sok, nem elhanyagolható kölcsönhatás miatt a direkt-szimuláció hamar nehézségekbe ütközik. Ezért érdemes bevezetni olyan finomításokat, mint például a léptetési idő variálása: minden részecske saját időlépéssel rendelkezik, így a különböző dinamikájú részecskéket nem kell minden időpillanatban léptetni.
Emellett létezik két alapvető, elterjedt algoritmus, melyek különböző módon egyszerűsítik a rendszert:
- Fa-algoritmusok (Tree methods):
A Tree method lényege, hogy a teret köbös cellákra osztják (octree): első lépésben 8 kockára osztják a teret, majd a megadott mélységig a cellákat tovább osztják 8 részre (az első lépéshez hasonlóan). Ha a felbontás indexelése következetes, akkor a hierarchia miatt minden cella egyértelműen címezhető (pl. "138" az első cella 3. cellájának 8. cellája). A felbontás után csak a szomszédos/közeli cellák részecskéire számolják individuálisan a kölcsönhatást. A távolabbi cellákat egy részecskeként veszik figyelembe, melyet a cella össztömege reprezentál annak tömegközéppontjában.
(Hasonló tér-felosztást lehet elérni szimulációk során a KD-tree binári felbontással. A GADGET azonban pl az octree-t használja.)
- Részecske-háló (Particle mesh method - PM method):
A PM method-ban a teret diszkretizálják egy ráccsal, és kiszámolják a gravitációs-potenciált a Poisson-egyenlet segítségével a rácspontokra:
ahol G a Newton-konstans, 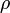 pedig a sűrűség (a rácspontban lévő részecskék száma). Ez az egyenlet könnyen kezelhető FFT után a frekvencia térben:
pedig a sűrűség (a rácspontban lévő részecskék száma). Ez az egyenlet könnyen kezelhető FFT után a frekvencia térben:
ahol 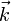 az együtt-mozgó hullámszám-vektor (kalap jelöli a Fourier-transzformáltat). Ezek után
az együtt-mozgó hullámszám-vektor (kalap jelöli a Fourier-transzformáltat). Ezek után 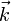 -val szorozva és inverz Fourier-transzformálva megkapható a gravitációs-tér. Mivel a rács mérete korlátozza ezt a módszert, ezért a kis-skálás erők számításához általában más módszerekkel kombinálva alkalmazzák ezt az eljárást. (Néha adaptív rácsozást is alkalmaznak, ami nagyobb sűrűségnél nagyobb rács-felbontást jelent.)
-val szorozva és inverz Fourier-transzformálva megkapható a gravitációs-tér. Mivel a rács mérete korlátozza ezt a módszert, ezért a kis-skálás erők számításához általában más módszerekkel kombinálva alkalmazzák ezt az eljárást. (Néha adaptív rácsozást is alkalmaznak, ami nagyobb sűrűségnél nagyobb rács-felbontást jelent.)
- (Ezen módszerek természetesen más N-test szimulációs területeket is használatosak lehetnek, mint pl gázok, folyadékok szimulációjakor...)
Meg lehet említeni a GADGET-2 szimulációs programot, melyben található egy hibrid módszer is: a Tree és PM kombinációja (TreePM)
A Metropolis algoritmus
A Metropolis algoritmus egy eljárás, amivel bonyolult valószínűségi eloszlások mintavételezhetőek. Másképp megfogalmazva szeretnénk előállítani egy 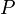 eloszlást, a kérdés az, hogy milyen átmeneti valószínűségekkel
eloszlást, a kérdés az, hogy milyen átmeneti valószínűségekkel 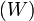 vezérelt folyamat (egészen pontosan Markov-folyamat) vezet ilyenre? A módszer kihasználja a részletes egyensúly elvét, ez esetünkben azt jelenti, hogy:
vezérelt folyamat (egészen pontosan Markov-folyamat) vezet ilyenre? A módszer kihasználja a részletes egyensúly elvét, ez esetünkben azt jelenti, hogy:
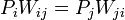 teljesül minden
teljesül minden 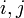 -re.
-re.
Ez még kevés feltétel az átmeneti valószínűségekre, ezért a Metropolisz megkötés a következő:
Bár általánosan tetszőleges eloszlás előállítható, fizikában általában valamilyen egyensúlyi eloszlást szeretnénk előállítani. Például, ha termális egyensúlyt szeretnénk, akkor 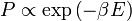 , és a Metropolisz megkötésben szereplő hányados is exponenciális alakban írható. A
, és a Metropolisz megkötésben szereplő hányados is exponenciális alakban írható. A 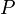 -t előállító eljárás a következő:
-t előállító eljárás a következő:
- Induljunk ki egy A konfigurációból.
- Állítsuk elő a megváltoztatott B konfigurációt.
- Számoljuk ki erre a két konfigurációra a megkötésben szereplő hányadost.
- Generáljunk egy 0-1 intervallumon vett egyenletes eloszlású véletlen számot: X.
- Ha
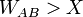 akkor a B konfigurációt fogadjuk el, ellenkező esetben marad az A.
akkor a B konfigurációt fogadjuk el, ellenkező esetben marad az A. - Ismételjük 1-től.
A Monte-Carlo módszer
A Monte-Carlo módszernek nevezzük az olyan eljárásokat, amelyek a problémákat random számok és valószínűségek felhasználásával oldják meg. Az eljárás során ismétlődően kiértékelünk egy determinisztikus modellt, random számokat használva inputnak. Akkor használják, ha a feladat nagyon összetett, nemlineáris, bonyolultak a határfeltételei, vagy nagyon sok paramétertől függ, illetve sok dimenziós.
Használata:
- Állítsuk föl a modellt: y = f(x1, x2, ..., xq)
- Generáljunk random számokat inputnak: xi1, xi2, ..., xiq
- Értékeljük ki a modellt, az eredményt tároljuk el yi-ben
- Ismételjük a 2. és 3. lépéseket n-szer
- Elemezzük az eredményeket hisztogram, összesítő statisztikák, stb. segítségével
- Klasszikus példa a
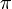 kiszámítása:
kiszámítása:
Rajzoljunk egy r sugarú kört és egy köré írt négyzetet (2r oldalú). Ha véletlenszerűen mintavételezzük a négyzet területét, akkor a körben lévő pontok száma úgy aránylik a körben és négyzetben lévő pontok számához (tehát az összeshez), mint a síkidomok terülte. Így 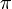 közelítőleg felírható egy hányadossal:
közelítőleg felírható egy hányadossal:
Itt is egyszerűen belátható, hogy a több mintavételezési pont pontosabb értéket eredményez.
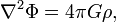
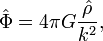
![W_{ij} = \mathrm{min}\left[1, \frac{P_j}{P_i} \right]](/images/math/a/d/1/ad1920c41b7e81ab4a74e9500c031123.png)