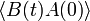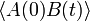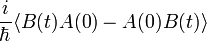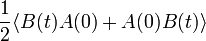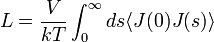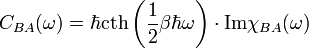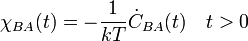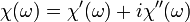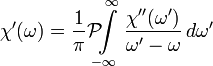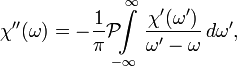Válasz- és korrelációs függvények, fluktuáció-disszipáció tétel '12
Ebbe a tételbe sok minden a Sasi-féle Nemegyensúlyi Statisztikus Fizika órából fog bekerülni.
Tartalomjegyzék
Lineáris válasz-elmélet
Kis külső perturbáció hatására a legkülönbözőbb fizikai rendszerek által produkált reakciók is jól tárgyalhatók lineáris közelítésben. Ide értendőek nem csak a korábban tárgyalt transzport jelenségek, de maguk a mérések is: például mechanikai vagy termodinamikai változásnak teszünk ki egy rendszert egy 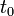 időpontban és megmérjük a különböző jellemzőit egy
időpontban és megmérjük a különböző jellemzőit egy 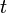 időpontban. A rendszert leíró fizikai jellemzők itt is első rendben lineáris kapcsolatba hozhatóak a perturbációval.
időpontban. A rendszert leíró fizikai jellemzők itt is első rendben lineáris kapcsolatba hozhatóak a perturbációval.
A tárgyaláshoz legyen az izolált (nem-perturbált) rendszer Hamiltonja 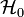 és a kölcsönhatást leíró Hamilton
és a kölcsönhatást leíró Hamilton 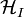 , valamint a teljes rendszert jellemző Hamilton ezek összege. Tételezzük fel a külső perturbációról nem csak azt, hogy gyenge, de azt is, hogy adiabatikusan kapcsoljuk be, azaz nagyon lassan, kvázi-stacionárius állapotokon keresztül.
, valamint a teljes rendszert jellemző Hamilton ezek összege. Tételezzük fel a külső perturbációról nem csak azt, hogy gyenge, de azt is, hogy adiabatikusan kapcsoljuk be, azaz nagyon lassan, kvázi-stacionárius állapotokon keresztül.
A rendszert jellemezzük a sűrűségoperátorral, 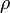 -val. Egy
-val. Egy 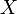 mennyiség átlaga (sokaság és kvantum átlag)
mennyiség átlaga (sokaság és kvantum átlag) 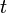 időpontban:
időpontban:
ahol 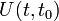 az időfejlesztés unitér operátora, amely leírja a rendszert jellemző mennyiségek időfejlődését
az időfejlesztés unitér operátora, amely leírja a rendszert jellemző mennyiségek időfejlődését 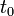 -ból
-ból 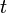 -be. A kölcsönhatási képben minden operátor (így
-be. A kölcsönhatási képben minden operátor (így 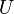 is) a szabad Hamilton szerint fejlődik időben:
is) a szabad Hamilton szerint fejlődik időben:
Ennek a megoldása 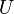 -ra egy exponenciális kifejezést ad, amit első rendig sorfejtve kapjuk, hogy:
-ra egy exponenciális kifejezést ad, amit első rendig sorfejtve kapjuk, hogy:
Ezt beírva az X mennyiség átlagának képletébe, és kihasználva a Tr ciklikusságát, valamint, hogy kezdetben a rendszer egyensúlyi állapotát a kanonikus eloszlás írta le: 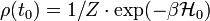 , továbbá a külső perturbációja legyen
, továbbá a külső perturbációja legyen 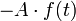 alakú, ahol
alakú, ahol 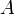 a perturbáló mennyiség operátora,
a perturbáló mennyiség operátora, 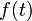 pedig a perturbáció amplitudója. Mindezekkel kapjuk:
pedig a perturbáció amplitudója. Mindezekkel kapjuk:
Mivel a Tr alatti ciklikus permutációs szimmetria van érvényben, az időfüggések átcsoportosíthatóak, ezért a []-es mennyiség csak az időkülönbségtől függ. Ezekkel kapjuk a Kubo-formulát:
ahol:
a szuszceptibilitás, vagy lineáris válasz függvény, a jobboldalon a második szögletes zárójel már kommutátort jelöl, a várhatóérték pedig a sokaságátlagot jelenti.
Nemegyensúlyi izoterm lineáris válsz
Ha nemegyensúlyi sokrészecskés kvantumrendszerre szeretnénk levezetni a lineáris választ (időfüggetlen, azaz sztatikus esetben), ahol nem ismert, hogy az állapotösszeg kicsit eltér az egyensúlyihoz képest, akkor ezt is sorfejteni kell a kölcsönhatás szerint. Itt most nem időfüggést vizsgálunk, hanem az egyensúlyi eloszlástól való eltérést. Eredményül azt kapjuk, hogy:
Itt az 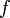 -et szorzó integrál
-et szorzó integrál 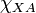 , az izoterm, sztatikus válaszfüggvény. A baloldali a nem-egyensúlyi (perturbált) várhatóértéke az X mennyiségnek, a jobboldali első tag az egyensúlyi várható érték. Ha akár a perturbáló, akár a rendszert jellemző operátor kommutál H-val, azaz megmaradó mennyiség, akkor az integrálból egy
, az izoterm, sztatikus válaszfüggvény. A baloldali a nem-egyensúlyi (perturbált) várhatóértéke az X mennyiségnek, a jobboldali első tag az egyensúlyi várható érték. Ha akár a perturbáló, akár a rendszert jellemző operátor kommutál H-val, azaz megmaradó mennyiség, akkor az integrálból egy 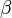 szorzó marad, ekkor a válaszfüggvény a korrelációs függvénnyel (alább az első def.) arányos, ez a fluktuáció-válasz tétel: tehát általánosan az izoterm lineáris válszt a korrelációs függvény
szorzó marad, ekkor a válaszfüggvény a korrelációs függvénnyel (alább az első def.) arányos, ez a fluktuáció-válasz tétel: tehát általánosan az izoterm lineáris válszt a korrelációs függvény 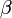 (inverz hőméréséklet) integrálja adja.
(inverz hőméréséklet) integrálja adja.
Lineáris válaszfüggvény és a transzport koefficiensek
Az egész elmélet azért is jelentős, mert a korábban tárgyalt transzport koefficiensek tulajdonképpen nem mások, mint a rendszer lineáris válaszai a megfelelő külső perturbációkra. Ennek megfelelően, például az elektromos vezetőre kapcsolt külső perturbáló tér esetén a váalszfüggvény a vezetőképesség tenzora lesz, ami így meghatározható a statsztikus átlagokból: a perturbáció operátora a polarizáció 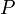 és a perturbáció amplitudója
és a perturbáció amplitudója 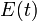 a külső elektromos tér, a rendszer válasza pedig az áramsűrűség. Ekkor az egyszerűség kedvéért izortop rendszerre:
a külső elektromos tér, a rendszer válasza pedig az áramsűrűség. Ekkor az egyszerűség kedvéért izortop rendszerre:
Korrelációs-függvények
A matematikában (a statisztikában) a korreláció jelzi két tetszőleges érték közötti lineáris kapcsolat nagyságát és irányát (avagy ezek egymáshoz való viszonyát). Az általános statisztikai használat során a korreláció jelzi azt, hogy két tetszőleges érték nem független egymástól. Az ilyen széles körű használat során számos együttható, érték jellemzi a korrelációt, alkalmazkodva az adatok fajtájához. A korreláció csak a lineáris kapcsolatot jelzi. Például egy valószínűségi változó és négyzete korrelációja lehet nulla. Ha két véletlen mennyiség korrelációja nulla, akkor korrelálatlanok; ilyenkor a kapcsolatot, ha van, másként kell jellemezni, például feltételes valószínűségekkel. A normális eloszlású valószínűségi változókra jellemző, hogy ha korrelálatlanok, akkor függetlenek is. Így a korreláció jól alkalmazható normális eloszlásúnak tekinthető mérhető mennyiségek közötti kapcsolat erősségének mérésére.
Két mennyiség korrelációs függvényét igen sokféle alakban fel lehet írni. Például:
Belátható, hogy ezek közül csak 1 függtelen van. Az utolsó az alábbiakban még hivatkozott 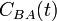 .
.
A korrelációs-függvények azért is fontosak, mert belőlük közvetlenül meghatározhatóak a lineáris transzport-koefficiensek. Ha 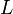 egy
egy 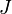 áramhoz tartozó transzport koefficiens, akkor a Green-Kubo formula alapján a kapcsolatuk:
áramhoz tartozó transzport koefficiens, akkor a Green-Kubo formula alapján a kapcsolatuk:
ahol a 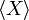 egyensúlyi átlag. Ezek a formulák csak egyensúlyi, végtelenül lassú (kvázistacionárius) folyamatokra érvényesek.
egyensúlyi átlag. Ezek a formulák csak egyensúlyi, végtelenül lassú (kvázistacionárius) folyamatokra érvényesek.
Fluktuáció-disszipáció tétel
Az alcímben említett tétel kapcsolatot állapít meg az egyensúly körüli ingadozást jellemző mennyiségek és az egyensúlyhoz való tartás sebessége között. Ennek felhasználásával tehát kizárólag az egyensúly körüli ingadozásból következtetést tudunk levonni a folyamat időbeli lefutására. Amennyiben nem vennénk figyelembe azegyensúly körüli fluktuációkat (vagy ha nem vagyunk képesek azokat megfelelő pon-tossággal mérni), azaz sztochasztikus helyett determinisztikus modellel dolgoznánk,nem tudnánk ilyen információra szert tenni.
A korrelációs-függvény és a lineáris válaszfüggvény között a Fourier-térben egyszerű alakú kapcsolat áll fent:
A korrelációs függvény az egyensúlyi fluktuációkat jellemzi, míg a lineáris válaszfüggvény képzetes része a rendszer irreverzibilis megváltozását (pl. disszipáció) jellemzi, amiközben törekszik az egyensúly felé.
Klasszikus határesetben azt kapjuk, hogy:
ahol a klasszikusság feltétele, hogy a rendszer átmenetei sokkal kisebb energiájúak legyenek, mint a hőmérsékleti fluktuációk jellemző energiái: 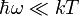
Ez a kapcsolat azést is fontos, mert a korrelációs-függvények aránylag könnyen mérhetők (pl: neutron-szórás kísérletek a nukleon-nukleon sűrűség korrelációs függvénnyel arányosak) ezáltal pedig megkaphatjuk a válaszfüggvény képzetes részét is. Magát a válszfüggvényt teljes egészében előállíthatjuk csupán a képzetes rész ismeretéből.
Kramers–Kronig-reláció
Matematikailag a Kramers–Kronig-reláció kapcsolatot teremt egy komplex függvény képzetes és valós része között, amennyiben a függvény analitikus a felső félsíkban. Fizikai rendszerek válaszfüggvényeinél a kauzalitás miatt ez a feltétel teljesül. A lineáris válszfüggvény Fourier-transzformáltja egy komplex mennyiség, írjuk fel tehát komplex alakban:
Ekkor a Kramers–Kronig-relációk:
és:
és 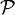 a főérték integrált jelöli.
a főérték integrált jelöli.
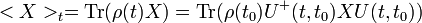
![i\hbar \frac{dU}{dt} = [U, \mathcal{H}_0]](/images/math/6/5/6/6560535c87f8094cac44301c2d173f61.png)
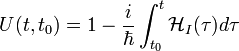
![\langle X \rangle_t = \langle X\rangle_0 + \frac{i}{\hbar}\int_{-\infty}^t d\tau \mathrm{Tr}\left[ \frac{\exp(-\beta\mathcal{H}_0)}{Z} (X(t)A(\tau)-A(\tau)X(t)) \right]f(\tau)](/images/math/a/a/e/aae87595587493a944327a00c350e75f.png)
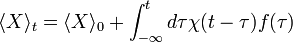
![\chi(t) = \frac{i}{\hbar}\mathrm{Tr}\left[ \frac{\exp(-\beta\mathcal{H}_0)}{Z} (X(t)A(0)-A(0)X(t)) \right]=\frac{i}{\hbar}\langle \left[ X(t), A(0) \right] \rangle_0](/images/math/d/a/a/daac7b8b42ad731d239dd50f8d959cb6.png)
![<X> = <X>_0 + \int_{0}^\beta ds \left[ \langle A(s)X \rangle_0 - \langle X \rangle_0 \langle A \rangle_0 \right] f](/images/math/a/7/8/a78248486c9bc37e80601a13ee5b4c53.png)
![\sigma(t) = \frac{1}{V} \chi_{JP}(t) = \frac{1}{V}\frac{i}{\hbar}\langle [J(t), P(0)] \rangle\,](/images/math/b/1/a/b1aec879ce2de0c0b5021362d79434b4.png)