Adatelemzés: lineáris és nem lineáris regresszió egy modellen bemutatva
Tartalomjegyzék
Általános statisztikai jellemzők
Alapfogalmak:
- Átlag: ha van N darab adatpontunk (egy X vektorba rendezve), mindegyiket
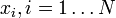 -vel jelöljük, akkor az átlag:
-vel jelöljük, akkor az átlag: ![E[X] = \mu = \bar{x} = \frac{1}{N} \sum_{i=1}^N x_i](/images/math/7/a/0/7a0451a68312c8535090611e6e6cb5b5.png)
- Szórás: ha van N db,
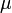 átlagú adatpontunk, akkor ezek szórása:
átlagú adatpontunk, akkor ezek szórása: ![\sigma = \sqrt{E\left[ X - \mu \right]^2}](/images/math/a/8/1/a818f8e2bcfa670e582930973ba6a62e.png)
- Kovariancia: a kovariancia megadja két egymástól különböző változó (X,Y) együttmozgását:
![\mathrm{Cov}(X,Y) = E \left[ \left( X - E[X] \right) \left( Y - E[Y] \right) \right] = E[XY] - E[X]\cdot E[Y]](/images/math/f/8/d/f8df991a614a68da224374938aa541c5.png)
- Kovariancia mátrix: egy n adatpontból álló X és egy m adatpontból álló Y véletlen (random) vektor n*m-es kovariancia mátrixa:
![\mathrm{Cov}(X,Y) = E\left[ \left( X - E[X] \right) \left( Y - E[Y] \right)' \right] = E[XY'] - E[X]E[Y]'](/images/math/4/3/1/4310f0ee1a703e49ad1d287efc48a4c9.png) , ahol
, ahol ![E[XY']](/images/math/6/7/b/67bea2f0d36ba09ac0a82591c8559b8b.png) ,
, ![E[Y]'](/images/math/5/8/6/5866ffb2a3efac4948038aa84920db0c.png) és
és ![E[X]](/images/math/f/5/6/f564e7c6618bc2c0c99eae5a9376fbaf.png) vektorok és általános esetben mindegyik elemük az X és Y vektor eredeti elemének várható értéke (amennyiben a vektor komponensei különböző eloszlású valószínűségi változók).
vektorok és általános esetben mindegyik elemük az X és Y vektor eredeti elemének várható értéke (amennyiben a vektor komponensei különböző eloszlású valószínűségi változók). - Keresztkorreláció: a keresztkorreláció segítségével megvizsgálhatjuk két adatsor hasonlóságát különböző időeltolásokra. Folytonos függvény esetén a definíció:
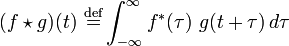 , diszkrét adatpontok esetén pedig:
, diszkrét adatpontok esetén pedig: ![(f \star g)[n]\ \stackrel{\mathrm{def}}{=} \sum_{m=-\infty}^{\infty} f^*[m]\ g[n+m]](/images/math/d/6/d/d6dcf7787d5212b60954084127156aa9.png) . Két fehér zaj függvény vagy vektor keresztkorrelációs függvénye egy Dirac-delta.
. Két fehér zaj függvény vagy vektor keresztkorrelációs függvénye egy Dirac-delta. - Normált kereszt-korreláció:
- Autokorreláció:
(Átlag szórás, kovariancia...)
Modellek illesztése
Lineáris regresszió
A most leírt modell tulajdonságai a következők:
- prediktor változó: x
- az y-ok függetlenek
- adott x-re kapott y-ok normál eloszlásúak olyan átlaggal, ami az x lineáris függvényeként kapható meg
- Feladat: adott x-re y-t megmondani. A straight line regression model (egyenes vonal illesztő modell) alakja a köv:
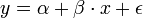 , vagy indexesen
, vagy indexesen 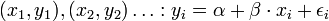
A normál analízis során azt feltételezzük, hogy epsilon_i-k független és azonosan 0 átlagú és szigma^2 szórású normál eloszlást követő változók. Az alfa+beta*x a determinisztikus rész, az epsilon_i a random zaj. Az előbbi érdekel minket.
Az illesztés során a legkisebb négyzetek módszerét használhatjuk.
Legkisebb négyzetek módszere
A legkisebb négyzetek módszere bevezet egy metrikát arra nézve, hogy egy adott becslés az ismertelen 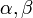 paraméterekre mennyire optimális. Ezt a mértéket következő költségfüggvény adja meg:
paraméterekre mennyire optimális. Ezt a mértéket következő költségfüggvény adja meg:
azaz a legkisebb négyzetes eltérést eredményező paraméter értékeket keressük. Legegyszerűbben úgy találhatjuk meg ezt a minimumot, hogy a paraméterek szerint lederiváljuk a költségfüggvényt, és a kapott kifejezést 0-val tesszük egyenlővé, és a kapott egyenletrendszert megoldjuk. Az eredmény:
ahol a felülvonás átlagolást jelent az n mérésen, a kalap pedig a módszer által adott becslést az adott paraméterre. Természetesen a levezetés általánosítható arra az esetre is, ha x több komponensű. Általánosabb költségfüggvényű módszerek is egyszerűen származtathatóak. Az x és y értékek korrelációját r adja:
ahol 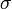 a minta standard hibája. r értéke 1 ha tökéletes lineáris korreláció van, -1 ha tökéletes antikorreláció. A fit jóságát R^2 adja:
a minta standard hibája. r értéke 1 ha tökéletes lineáris korreláció van, -1 ha tökéletes antikorreláció. A fit jóságát R^2 adja:
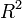 -et 1 ha tökéletesen lineárisak az adatok, általában a 0,95 körüli érték elfogadható fit szokott lenni.
-et 1 ha tökéletesen lineárisak az adatok, általában a 0,95 körüli érték elfogadható fit szokott lenni.
A Khí-négyzet módszer
Ha a mérési pontok hibájának szórása nem egyforma (de továbbra is normál eloszlást követnek), akkor a legkisebb négyzetek módszerét könnyen általánosíthatjuk. Ez a Khí-négyzet illesztés, amelynek költségfüggvénye a következő:
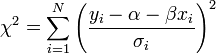
Tekinthetjük úgy, hogy a 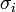 szórásokkal súlyozzuk az eltéréseket, vagy másképpen egységnyi szórásúra normálunk minden pontnál.
szórásokkal súlyozzuk az eltéréseket, vagy másképpen egységnyi szórásúra normálunk minden pontnál.
Mivel a mérési pontokról feltételeztük, hogy normál eloszlást követnek, 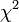 ilyen véletlen változók négyzetének összege. Az ilyen típusú valószínűségi változók nem Gauss eloszlást, hanem az úgynevezett (N - M) szabadsági fokú Khí-négyzet eloszlást követik. Ha az
ilyen véletlen változók négyzetének összege. Az ilyen típusú valószínűségi változók nem Gauss eloszlást, hanem az úgynevezett (N - M) szabadsági fokú Khí-négyzet eloszlást követik. Ha az 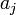 paraméterek lineárisan szerepelnek akkor ez az eloszlás analitikusan megadható, így megmondható annak valószínűsége (Q), hogy az adott paraméterekkel jellemzett modellen végzett mérés
paraméterek lineárisan szerepelnek akkor ez az eloszlás analitikusan megadható, így megmondható annak valószínűsége (Q), hogy az adott paraméterekkel jellemzett modellen végzett mérés 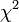 -nél nagyobb eltérést ad. (
-nél nagyobb eltérést ad. (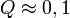 tipikus,
tipikus, 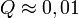 elfogadható,
elfogadható, 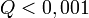 rossz modellre vagy hibabecslésre utal). Fontos, hogy a mérési hibák becslése jó legyen, különben megtévesztő eredményre juthatunk.
rossz modellre vagy hibabecslésre utal). Fontos, hogy a mérési hibák becslése jó legyen, különben megtévesztő eredményre juthatunk.
A levezetés lépései teljesen azonosak az előző esettel.
Példa: egyenes illesztés
Legegyszerűbb példa a lineáris regresszióra a kétparaméteres egyenesillesztés.
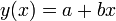
A költségfüggvényünk most:
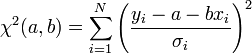
A minimumban a deriváltak eltűnnek:
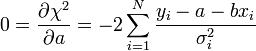
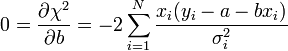
A fenti kifejezésekben a szummákat szétbonthatjuk az alábbi jelölések segítségével:
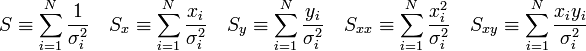
Így a minimum feltétele a következő:
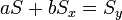
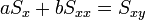
Az egyenletrendszer megoldása pedig:
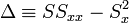
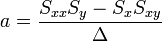
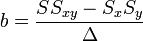
A hibaterjedés törvényét figyelembe véve a teljes szórás:
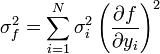
Amibe a-t és b-t behelyettesítve:
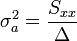
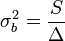
Ezek a hibák természetesen csak a mérési hibák hatását fejezik ki, ettől a pontok szórhatnak messze az egyenestől. Az illesztés jóságát az (N-2) szabadsági fokú khí-négyzet eloszlás adja meg a 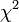 helyen.
helyen.
Ha a mérés hibája nem ismert, akkor a fenti képletek a 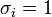 behelyettesítéssel használhatók (úgy tekintjük, hogy mindegyik pont hibája megegyezik).
behelyettesítéssel használhatók (úgy tekintjük, hogy mindegyik pont hibája megegyezik).
Maximum Likelihood
A maximum likelihood a legvalószínűbb becslést adja egy tetszőleges eloszlás paramétereire. Ha 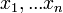 megfigyelésünk van, és egy
megfigyelésünk van, és egy 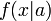 modellt szeretnénk fittelni, akkor független és azonos eloszlású minták esetén a feltételes valószínűség faktorizálható, azaz annak a valószínűsége, hogy az x mérési pontokat kaptuk feltéve, hogy a modell paraméterrendszere a:
modellt szeretnénk fittelni, akkor független és azonos eloszlású minták esetén a feltételes valószínűség faktorizálható, azaz annak a valószínűsége, hogy az x mérési pontokat kaptuk feltéve, hogy a modell paraméterrendszere a:
Ha megfordítjuk a logikát és azt kérdezzük, hogy feltéve, hogy x értékeket mértünk, mi a valószínűsége annak, hogy a modellt az a paraméterek jellemzik, akkor a likelihood függvényt kapjuk:
vagy ha vesszük a logaritmusát:
A legjobb becslést L (vagy ekvivalensen ln L) maximuma adja. Ha f a normális eloszlás, akkor könnyen kiszámolható a maximum a paraméterek szerinti deriváltak zérussá válásából. Ebből a szokásos értékeket kapjuk az átlagra (mérések összege / elemszám) és a szórásra (átlagtól való négyzetes eltérések átlaga).
Nem-lineáris regresszió
Amennyiben a modell paraméterek a modellben nem-lineáris alakban szerepelnek, akkor a fenti módszerek nem működnek, ez vezet a nem-lineáris regresszió problémájára. Ez többek között azt is jelenti, hogy nincs garantálva, hogy egyetlen globális optimum van, ezért a megoldások analitikusan általában nem kezelhetők: csak numerikus közelítő eljárásokkal tudjuk előállítani a legjobb becsléseket.
Léteznek megfelelő általánosításai a legkisebb négyzetek módszerének nemlineáris esetekre, csak úgy, mint a legtöbb más modellnek is.
Szemléletesen ha a modell összefüggését a paraméterekkel az f függvény adja, akkor a paraméterek szerinti deriválásoknál megjelenik f deriváltja is.
Nem-lineáris legkisebb négyzetek módszere
A költségfüggévny:
a derivált:
Az így kapható egyenletrendszer nem-lineáris, ezért általában valamilyen iterációs módszerrel lehet csak kezelni, például a Newton-iteráció általánosítható nem-lineáris egyenletrendszerek megoldására.
![\mathrm{min}_{\alpha, \beta}\left( \sum_{i=1}^N [y_i - \alpha - \beta x_i]^2 \right)](/images/math/5/b/0/5b04998ecac22704640d9b05a3573fa2.png)
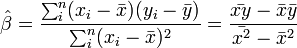
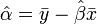
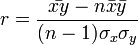
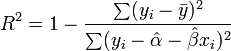

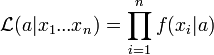
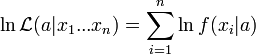
![S = \sum_i^n \left[ y_i - f(a, x_i)\right]^2](/images/math/c/6/6/c662329954f55b78d773ee1dec743c84.png)
![\frac{\partial S}{\partial a} = -2 \sum_i^n \left[ y_i - f(a, x_i)\right] \frac{\partial f(a, x_i}{\partial a} = 0](/images/math/f/4/a/f4a607a3967f3f60022c7206d0fa7f02.png)