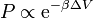„Dinamikai rendszerek, kaotikus viselkedés '12” változatai közötti eltérés
(Új oldal, tartalma: „== Dinamikai rendszerek elmélete == A dinamikai rendszerek elmélete csatolt differenciálegyenletek tulajdonságával foglalkozik, amiknek az időfejlődését néhány …”) |
|||
| (2 közbenső módosítás, amit 2 másik szerkesztő végzett, nincs mutatva) | |||
| 13. sor: | 13. sor: | ||
====Attraktor==== | ====Attraktor==== | ||
A fázistér vonzó halmaza, vagyis olyan halmaza, amely felé a trajektóriák közelednek. Disszipatív rendszerekben fordulnak elő, fázistérfogatuk zérus. | A fázistér vonzó halmaza, vagyis olyan halmaza, amely felé a trajektóriák közelednek. Disszipatív rendszerekben fordulnak elő, fázistérfogatuk zérus. | ||
| + | ====Intermittencia==== | ||
| + | Ez azt jelenti, hogy bizonyos paraméter értékeknél a kaotikus tartományban is sokáig szabályosan viselkedik a rendszer , majd visszavált kaotikussá. | ||
== Determinisztikus káosz == | == Determinisztikus káosz == | ||
| 22. sor: | 24. sor: | ||
A legismertebb példája a determinisztikus káosznak a logisztikus leképzés. Ezt nem differenciálegyenlettel írjuk le, hanem a másik lehetséges módon, leképezés formában, ami a következő: <math>x_{n+1} = r\,x_n(1-x_n)</math>. Az x változó a [0:1] tartományon értelmezhető, az r paraméter pedig [0:4] lehet. A leképezést populációdinamikai modellekben szokták használni, ahol x a populáció hányada a teljes lehetséges populációhoz, az r pedig a szaporodási és a pusztulási ráta kombinációja. Az x<sub>n</sub> sorozat viselkedését az r paraméter határozza meg. Ha r<3, akkor 1 fixpont van, ha 3<r<3.4, akkor 2 fixpont van, stb. Hogy melyik r értéknél milyen viselkedést tapasztalunk, a [http://en.wikipedia.org/wiki/File:LogisticMap_BifurcationDiagram.png bifurkációs diagramról] olvashatjuk le. Még több a logisztikus leképezésről [http://en.wikipedia.org/wiki/Logistic_map itt]. | A legismertebb példája a determinisztikus káosznak a logisztikus leképzés. Ezt nem differenciálegyenlettel írjuk le, hanem a másik lehetséges módon, leképezés formában, ami a következő: <math>x_{n+1} = r\,x_n(1-x_n)</math>. Az x változó a [0:1] tartományon értelmezhető, az r paraméter pedig [0:4] lehet. A leképezést populációdinamikai modellekben szokták használni, ahol x a populáció hányada a teljes lehetséges populációhoz, az r pedig a szaporodási és a pusztulási ráta kombinációja. Az x<sub>n</sub> sorozat viselkedését az r paraméter határozza meg. Ha r<3, akkor 1 fixpont van, ha 3<r<3.4, akkor 2 fixpont van, stb. Hogy melyik r értéknél milyen viselkedést tapasztalunk, a [http://en.wikipedia.org/wiki/File:LogisticMap_BifurcationDiagram.png bifurkációs diagramról] olvashatjuk le. Még több a logisztikus leképezésről [http://en.wikipedia.org/wiki/Logistic_map itt]. | ||
| + | |||
| + | == A logisztikus leképezés == | ||
| + | A logisztikus leképezés a kaotikus rendszerek állatorvosi lova. Tulajdonképpen egy egyszerű populációdinamikai modell, a farkasok és a nyulak populációjának esetére. A függvény a fázistér (nyulak és farkasok populációja) egy Poincaré-mettszetét adja. A leképezést a következőképpen definiáljuk: | ||
| + | |||
| + | <math>x_{n+1}=r*x_n(1-x_n)</math> vagy <math>F(x)=r*x(1-x)</math> | ||
| + | |||
| + | A rendszer érdekessége hogy r értékének megválasztásától függően változatos, (ki gondolná) kaotikus viselkedést mutat. | ||
| + | |||
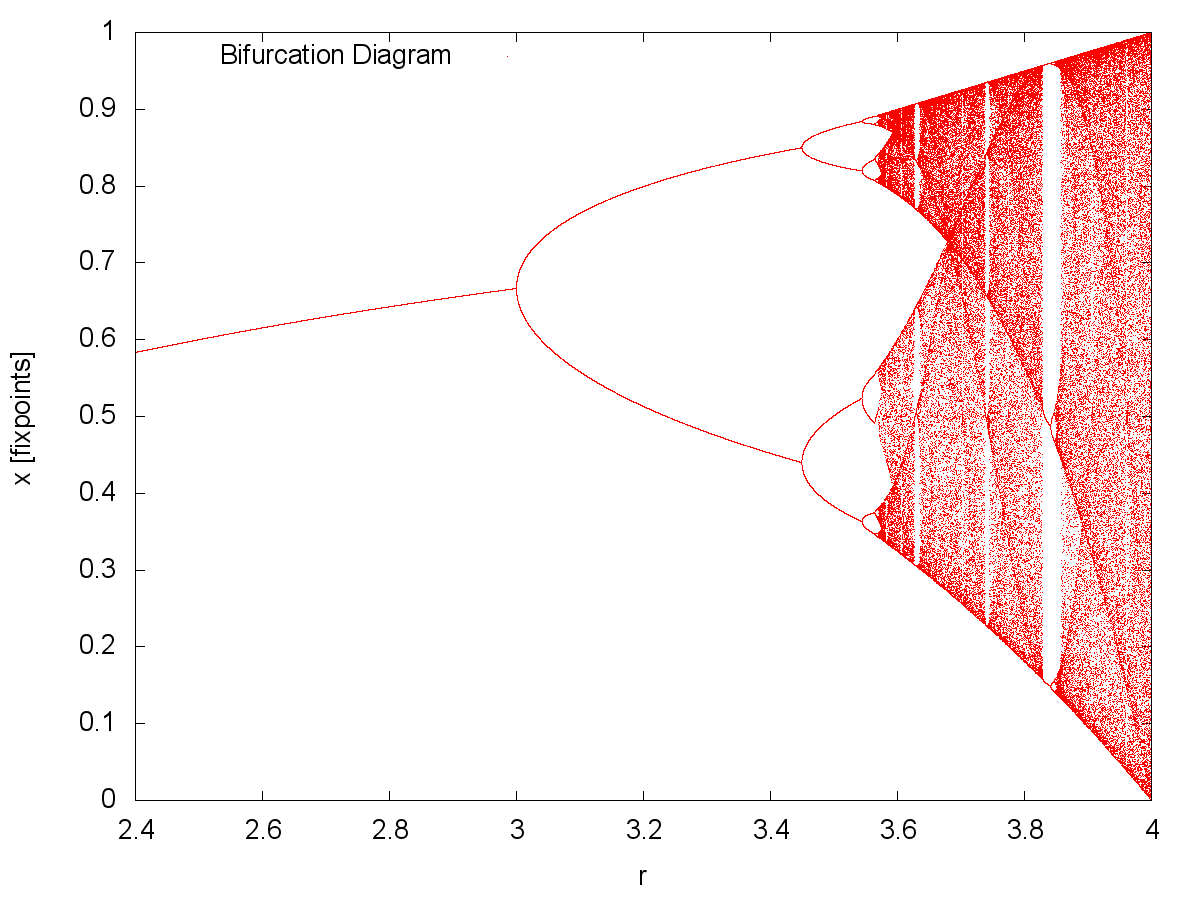
| + | Ha <math>r<1=r_1</math>, akkor minden kezdőállapotból indítva <math>x_n</math> -> 0 , ez a rendszer egyedüli fixpontja (x_1^*). Ha r-et 1 fölé növeljük, akkor megjelenik egy másik fixpont is: <math>x_2^*=\frac{r-1}{r}</math>, és ezzel egyidőben <math>x_1^*</math> instabillá válik. Egyszerűen kiszámítható, hogy van olyan <math>r_2(=3)</math>, hogy <math>r>r_2</math> értékekre <math>x_2*</math> is instabil lesz. Ekkor azonban a leképezés második iteráltjának (<math>F^{(2)}(x) = F(F(x))</math>) megjelenik két stabil fixpontja ( <math>x_3^*</math>, <math>x_4^*</math>). Az attraktort ez a két fixpont fogja alkotni, és mivel <math>x_3^*=F(x_4^*)</math> és <math>x_4^*=F(x_3^*)</math> ezért a nyulak száma két éves periódussal oszcillálni fog. Ezt a változást az időfejlődésben - azaz a periódusidő hirtelen 1 év 2 év átmenetét - nevezzük bifurkációnak.r-et tovább növelve egyre nagyobb periódushosszú lesz az attraktor (<math>2^k\rightarrow 2^{k+1}</math>), végül egy kritikus <math>r_{\infty}\approx3.5699</math> értéknél ez a hossz divergál: a rendszer kaotikus lesz. Ez a bifurkáció sorozat a kaotikussá válás egyik leggyakrabban előforduló módja és Feigenbaum-szekvenciának nevezik. | ||
| + | |||
| + | {| | ||
| + | |- | ||
| + | |[[Kép:Cobweb.png|center|350px|thumb|Cobweb diagram különböző ''r''-értékekre]]||[[Kép:BifurcationDiagram.png|center|450px|thumb|Bifurkációs diagram]] | ||
| + | |} | ||
== Káosz disszipatív rendszerekben == | == Káosz disszipatív rendszerekben == | ||
A lap jelenlegi, 2012. június 15., 11:05-kori változata
Tartalomjegyzék
Dinamikai rendszerek elmélete
A dinamikai rendszerek elmélete csatolt differenciálegyenletek tulajdonságával foglalkozik, amiknek az időfejlődését néhány paraméter határozza meg. A rendszer időfejlődésének vizsgálata a paraméterek állapotterében zajlik.
Alapfogalmak
Fixpont és határciklus
Fixpontnak azt nevezzük, amikor a rendszer hosszú idő után a fázistér egy pontjában található meg. A fixpont lehet stabil (kis kitérésre visszatér), és instabil (kis kitérésre nem tér vissza). A határciklus a fázistérben egy zárt trajektória, amin a rendszer az idő előrehaladtával körbejár. Szintén lehet stabil vagy instabil.
Bifurkáció
Bifurkációról akkor beszélünk, amikor egy külső paraméter hatására a rendszer hosszú távú viselkedése kvalitatívan megváltozik (pl.: 1 fixpont → 2 fixpont, fixpont → határciklus, stb.)
Poincaré-metszet
A rendszer időfejlődését, főleg ha az d>3 dimenziós, nagyon nehéz grafikusan ábrázolni. Ezért a fázistérnek és egy síknak a metszetét vizsgáljuk. Ha egy közel periodikus pálya metszi a síkot (a fázistér egy alterét), akkor egy periódusidő múlva újra metszeni fogja, közel az előző ponthoz. Belátható, hogy egy pálya akkor periodikus, ha a Poincaré-metszetnek fixpontja.
Ljapunov-exponens
A Ljapunov-exponenssel az számszerűsíthetjük, hogy a fázistérben két közeli trajektória milyen gyorsan távolodik egymástól. Ha kezdetben 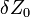 távolságra voltak, akkor az időben a távolságuk
távolságra voltak, akkor az időben a távolságuk 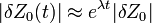 szerint növekszik.
szerint növekszik.
Attraktor
A fázistér vonzó halmaza, vagyis olyan halmaza, amely felé a trajektóriák közelednek. Disszipatív rendszerekben fordulnak elő, fázistérfogatuk zérus.
Intermittencia
Ez azt jelenti, hogy bizonyos paraméter értékeknél a kaotikus tartományban is sokáig szabályosan viselkedik a rendszer , majd visszavált kaotikussá.
Determinisztikus káosz
Az egyszerű, kevés összetevőből álló rendszerek szabálytalan mozgását kaotikusnak nevezzük. Jellemzői:
- nem ismétli önmagát
- nem jelezhető előre, mert érzékeny a kezdőfeltételekre, melyeket véges pontossággal ismerünk
- a visszatérési szabály bonyolult geometriájú (pl.: hely-sebesség ábrázolásban egy komplex, de szabályos szerkezet jelenik meg)
A valós folyamatok leírásában (egyszerű rendszerekre, pl.: kettős inga) fel tudjuk írni a rendszert mozgató differenciálegyenleteket, viszont a kezdőfeltételeket csak valamekkora hibával ismerjük. Mivel a kaotikus mozgás hibaerősítő, a mozgást a rövid előrejelzési időn túl követve a bizonytalanság eléri az egész attraktor méretét. Az ilyen mozgás tehát előre jelezhetetlen,rendszerint a fázistér fraktálalakzataihoz kötött, és hosszú távú leírása egy időfüggetlen valószínűségeloszlással lehetséges.
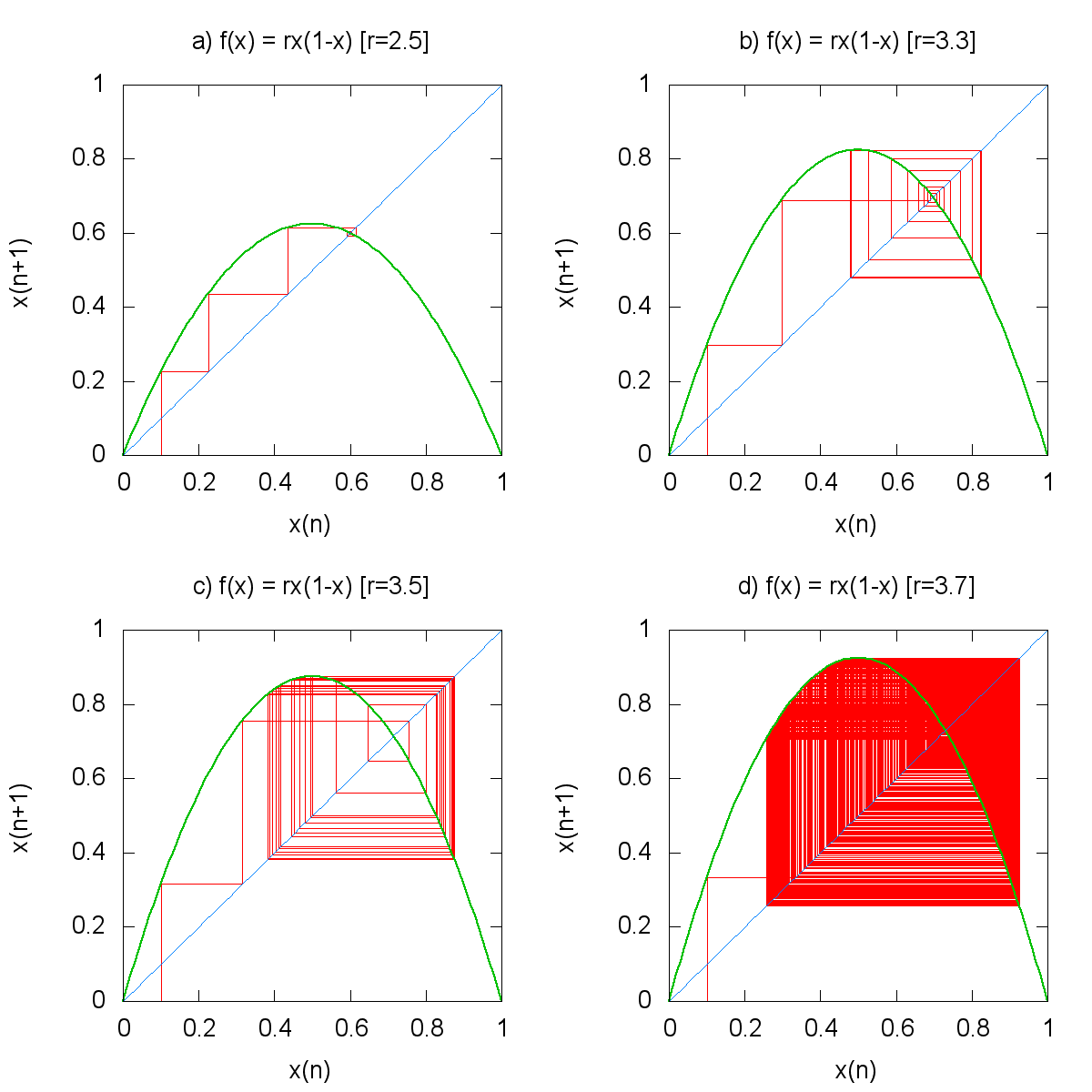
A legismertebb példája a determinisztikus káosznak a logisztikus leképzés. Ezt nem differenciálegyenlettel írjuk le, hanem a másik lehetséges módon, leképezés formában, ami a következő: 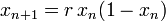 . Az x változó a [0:1] tartományon értelmezhető, az r paraméter pedig [0:4] lehet. A leképezést populációdinamikai modellekben szokták használni, ahol x a populáció hányada a teljes lehetséges populációhoz, az r pedig a szaporodási és a pusztulási ráta kombinációja. Az xn sorozat viselkedését az r paraméter határozza meg. Ha r<3, akkor 1 fixpont van, ha 3<r<3.4, akkor 2 fixpont van, stb. Hogy melyik r értéknél milyen viselkedést tapasztalunk, a bifurkációs diagramról olvashatjuk le. Még több a logisztikus leképezésről itt.
. Az x változó a [0:1] tartományon értelmezhető, az r paraméter pedig [0:4] lehet. A leképezést populációdinamikai modellekben szokták használni, ahol x a populáció hányada a teljes lehetséges populációhoz, az r pedig a szaporodási és a pusztulási ráta kombinációja. Az xn sorozat viselkedését az r paraméter határozza meg. Ha r<3, akkor 1 fixpont van, ha 3<r<3.4, akkor 2 fixpont van, stb. Hogy melyik r értéknél milyen viselkedést tapasztalunk, a bifurkációs diagramról olvashatjuk le. Még több a logisztikus leképezésről itt.
A logisztikus leképezés
A logisztikus leképezés a kaotikus rendszerek állatorvosi lova. Tulajdonképpen egy egyszerű populációdinamikai modell, a farkasok és a nyulak populációjának esetére. A függvény a fázistér (nyulak és farkasok populációja) egy Poincaré-mettszetét adja. A leképezést a következőképpen definiáljuk:
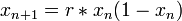 vagy
vagy 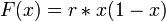
A rendszer érdekessége hogy r értékének megválasztásától függően változatos, (ki gondolná) kaotikus viselkedést mutat.
Ha 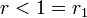 , akkor minden kezdőállapotból indítva
, akkor minden kezdőállapotból indítva 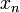 -> 0 , ez a rendszer egyedüli fixpontja (x_1^*). Ha r-et 1 fölé növeljük, akkor megjelenik egy másik fixpont is:
-> 0 , ez a rendszer egyedüli fixpontja (x_1^*). Ha r-et 1 fölé növeljük, akkor megjelenik egy másik fixpont is: 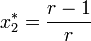 , és ezzel egyidőben
, és ezzel egyidőben 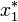 instabillá válik. Egyszerűen kiszámítható, hogy van olyan
instabillá válik. Egyszerűen kiszámítható, hogy van olyan 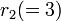 , hogy
, hogy 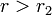 értékekre
értékekre 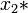 is instabil lesz. Ekkor azonban a leképezés második iteráltjának (
is instabil lesz. Ekkor azonban a leképezés második iteráltjának (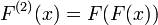 ) megjelenik két stabil fixpontja (
) megjelenik két stabil fixpontja ( 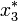 ,
, 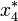 ). Az attraktort ez a két fixpont fogja alkotni, és mivel
). Az attraktort ez a két fixpont fogja alkotni, és mivel 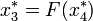 és
és 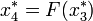 ezért a nyulak száma két éves periódussal oszcillálni fog. Ezt a változást az időfejlődésben - azaz a periódusidő hirtelen 1 év 2 év átmenetét - nevezzük bifurkációnak.r-et tovább növelve egyre nagyobb periódushosszú lesz az attraktor (
ezért a nyulak száma két éves periódussal oszcillálni fog. Ezt a változást az időfejlődésben - azaz a periódusidő hirtelen 1 év 2 év átmenetét - nevezzük bifurkációnak.r-et tovább növelve egyre nagyobb periódushosszú lesz az attraktor (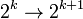 ), végül egy kritikus
), végül egy kritikus 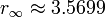 értéknél ez a hossz divergál: a rendszer kaotikus lesz. Ez a bifurkáció sorozat a kaotikussá válás egyik leggyakrabban előforduló módja és Feigenbaum-szekvenciának nevezik.
értéknél ez a hossz divergál: a rendszer kaotikus lesz. Ez a bifurkáció sorozat a kaotikussá válás egyik leggyakrabban előforduló módja és Feigenbaum-szekvenciának nevezik.
Káosz disszipatív rendszerekben
Disszipatív rendszerről akkor beszélünk, amikor a rendszer energiája súrlódás hatására folyamatosan csökken. Ha nem tudjuk a rendszerünket egy mechanikai rendszernek megfeleltetni, akkoronnan vehetjük észre a disszipációt, hogy a fázistérben a fázistérfogat csökken (nullához tart). Az egyik legegyszerűbb példa disszipatív rendszerre a súrlódásos matematikai inga:
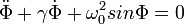
Az egyenletet fel lehet írni két elsőrendű, csatolt differenciálegyenletbe az 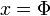 és az
és az 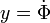 helyettesítéssel:
helyettesítéssel:
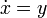
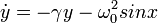
A fázistérfogat változását az alábbi egyenlet határozza meg:
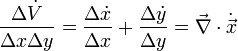
A disszipációt tehát úgy is megfogalmazhatjuk, hogy 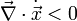
Hosszú idő elteltével a disszipáció egyedüli hatásként oda vezet, hogy a rendszer beáll egy infinitezinális pontba a fázistérben. Ha más hatás is van, az bizonyos irányokban ezt ellensúlyozhatja. Példa erre a Naprendszer(-ek) kialakulása: az összesűrűsödő porfelhő kezdetben gömbszimmetrikusan húzódik össze, azonban mivel csökken a tehetetlensége, forgása (ami kicsi mindig van a fluktuációk miatt) felgyorsul a perdületmegmaradás miatt. A növekvő sűrűség miatt azonban a surlódás (elemi rugalmatlan ütközések rátája) is nő, ezért egyre erősebb disszipáció lesz jellemző. A forgás és a disszipáció együtt oda vezet, hogy a fázitérfogatcsökkenés leghamarabb a forgás által kijelölt tengely mentén megy végbe, mert itt nincsenek ezt ellensúlyozó erőhatások. Ennek eredményeképpen jönnek létre a protoplanetáris korongok. Ez a tulajdonság általánosabb érvényű: a disszipáció redukálja a fázistér elérhető dimenzióinak számát.
Diffúzió
A determinisztikus diffúziót megfigyelhetjük a lökdösött rotátoron. Ez egy olyan rotátor, ami T időnként hirtelen impulzust kap (a lökés amplitúdója általában a hely periodikus függvénye, pl.: f(x) = a*sin x). A lökések amplitúdója bármilyen értéket felvehet a (-a,a) intervallumban, a sebesség változás ezért véletlen bolyongásnak fog megfelelni (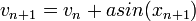 , ezért
, ezért 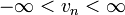 ). A sebességtengely 2
). A sebességtengely 2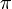 hosszúságú intervallumán nagy számú pontot indítva azt tapasztaljuk, hogy azok a vn tengely mentén egyre jobban szétterjednek. A kaotikus dinamika tehát egy diffúziós folyamatot hozott létre.
hosszúságú intervallumán nagy számú pontot indítva azt tapasztaljuk, hogy azok a vn tengely mentén egyre jobban szétterjednek. A kaotikus dinamika tehát egy diffúziós folyamatot hozott létre.
A bolyongás során egy részecske koordinátája az i-edik lépésben éppen 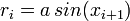 -gyel változik meg. Ha ri-k függetlennek tekinthetők, akkor az átlag elmozdulás
-gyel változik meg. Ha ri-k függetlennek tekinthetők, akkor az átlag elmozdulás 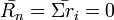 , a négyzetes átlagos elmozdulás pedig
, a négyzetes átlagos elmozdulás pedig 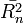 . A függetlenség miatt igaz, hogy
. A függetlenség miatt igaz, hogy 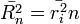 . A bolyongás diffúziós együtthatóját a
. A bolyongás diffúziós együtthatóját a 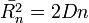 képletből kifejezhetjük:
képletből kifejezhetjük: 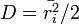 . Behelyettesítve ri értékét:
. Behelyettesítve ri értékét: 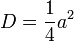 .
.
Mindebből tehát azt szűrhetjük le, hogy a determinisztikus eredetű mozgás elegendően hosszú idő alatt pont olyan folyamatot képes létrehozni, mint valamilyen külső zaj. Ez annak a megnyilvánulása, hogy a káosz véletlenszerű mozgást jelent, és ez jól definiált valószínűség-eloszlással jellemezhető. A diffúzió tehát arra nem érzékeny, hogy a bolyongást kiváltó hatás milyen eredetű.
Zajjal kölcsönható rendszerek
Ha egy egyébként determinisztikus rendszerhez egy külső zajt csatolunk, akkor azt áltlaánosan sztochsztikus rendszernek is nevezhetjük. Ezek számos helyen felbukkanhatnak, amikor bizonyos a rendszert érő hatásokat nem tudunk, vagy nem akarunk zárt alakban csatolni a leírásunkhoz, hanem csak valószínűségi változóként akarjuk a hatásukat figyelembe venni.
Sztochasztikus szökés
Tekintsünk egy részecskét, amely egy potenciál metastabil állapotában van, tehát létezik alacsonyabb állapotú helyzete, de azt egy potenciálgát miatt nem éri el. Ha erre a rendszerre egy külső zajforrást kapcsolunk, akkor ez bizonyos valószínűséggel fedezni tudja a gát legyőzéséhez szükséges energiakülönbséget, ezáltal a részecske el tudja hagyni a metastabil állapotot. Nem meglepő, hogy a metastabil potenciálgödröt harmonikus formában közelítve a szökés valószínűségére:
ahol 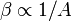 , ahol A a külső zaj amplitudója,
, ahol A a külső zaj amplitudója, 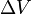 a potenciál gát magassága.
a potenciál gát magassága.
Sztochasztikus rezonancia
Tekintsünk egy két minimumú potenciálgödröt, amelyben mozgó részecskére zaj is hat, továbbá a potenciál minimumait perturbáljuk meg egy adott frekvenciájú amplitudóval. A zaj legyen olyan erős, hogy idnként át tudja lökni a rendszert egyik minimumból a másikba.
Amikor a zaj hatására történő minimum váltás tipikus periódusideje egyezik a perturbáció periódusidejével, akkor rezonancia lép fel: a külső zaj és a perturbáció hatására a részecske mindig el tud jutni az optimálisabb helyzetbe és periódusideje követi a potenciál változásának periódusát. Túl alcsony zajszintnél a rendszer beragad az egyik minimumba, túl magas zajszintnél elnyomja a külső gerjesztés hatását.
Hasonló folyamattal magyarázható esetleg a jégkorszakok közti változás: mind az eljegesedett, mind a jégmentes állapot stabil lenne (a plussz hő vagy elnyelődik az óceánokban, vagy visszaverődik a hóról), de a beeső sugárzás perioikusan változhat a Föld pályaelemeinek változásával, így előállhat a fenti időnként átbeillenő folyamat.