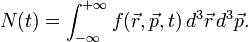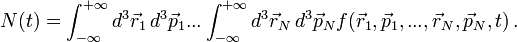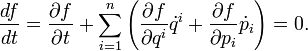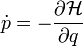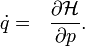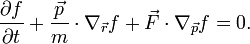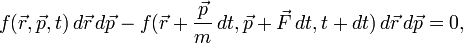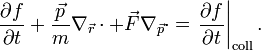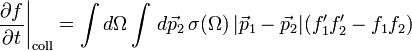„Soktest rendszerek” változatai közötti eltérés
(→Soktestrendszerek kontinuum leírása) |
|||
| 23. sor: | 23. sor: | ||
:<math>\dot q =~~\frac{\partial \mathcal{H}}{\partial p}.</math> | :<math>\dot q =~~\frac{\partial \mathcal{H}}{\partial p}.</math> | ||
| − | Fontos kiemelni, hogy a Liouville-egyenlet egy 6n dimenziós egyenlet (szemben a későbbiekkel). Tömören megfogalmazva a fázistérfogat megmaradását fejezi ki a mozgás trajektóriája mentén. | + | Fontos kiemelni, hogy a Liouville-egyenlet egy 6n dimenziós egyenlet (szemben a későbbiekkel). Tömören megfogalmazva a fázistérfogat megmaradását fejezi ki a mozgás trajektóriája mentén. Speciálisan 1 klasszikus részecskére az egyenlet: |
| + | |||
| + | :<math>\frac{\partial f}{\partial t}+\frac{\vec{p}}{m}\cdot\nabla_\vec{r}f+\vec{F}\cdot \nabla_\vec{p} f=0.</math> | ||
| + | |||
| + | === A Boltzmann-egyenlet === | ||
| + | A [http://en.wikipedia.org/wiki/Boltzmann_equation Boltzmann-egyenlet] Boltzmann-egyenlet az előzőekkel szemben az egyrészecske-eloszlásfüggvényre vonatkozó mozgásegyenletet adja meg. Alapvetően ez is a fázistérfogat megmaradására épít, amely külső erőhatás esetén ütközések nélkül: | ||
| + | |||
| + | :<math> | ||
| + | f(\vec{r},\vec{p},t)\,d\vec{r}\,d\vec{p} - f(\vec{r}+\frac{\vec{p}}{m}\,dt,\vec{p}+\vec{F}\,dt,t+dt)\,d\vec{r}\,d\vec{p} = 0, | ||
| + | </math> | ||
| + | |||
| + | A jobboldal az eloszlásfüggvény teljes deriváltja ha <math>d\vec{r} d \vec{p}</math> infinitezimális. Ha ütközések is vannak, azok a jobboldalra írhatóak. Ezekkel együtt a Boltzmann-egyenlet: | ||
| + | |||
| + | :<math> | ||
| + | \frac{\partial f}{\partial t} | ||
| + | + \frac{\vec{p}}{m} \nabla_\vec{r} \cdot | ||
| + | + \vec{F} \nabla_\vec{p} \cdot | ||
| + | = \left. \frac{\partial f}{\partial t} \right|_{\mathrm{coll}}. | ||
| + | </math> | ||
| + | |||
| + | Azaz az ütközési tagtól eltekintve visszakaptuk a Liouville-egyenlet fenti speciális esetét. Boltzmann nagy eredménye az volt, hogy az ütközési tagra is tudott jól használható feltevést tenni az egyrészecske-eloszlásfüggvényekkel kifejezve. Ez a molekuláris káosz feltevés, amely arra épül, hogy a részecskék sebességei korrelálatlanok az ütközés előtt és után, továbbá függetlenek a helytől. Ennek a segítségével az ütközési tag: | ||
| + | |||
| + | :<math> | ||
| + | \left. \frac{\partial f}{\partial t} \right|_{\mathrm{coll}} = \int d\Omega \int \, d\vec{p}_2 \, \sigma(\Omega) \, |\vec{p}_1 - \vec{p}_2| (f'_1 f'_2 - f_1 f_2) | ||
| + | </math> | ||
| + | |||
| + | ahol az 1, 2 indexek az egyik és másik részecske adatait indexelik, a vesszőtlen menyiségek az ütközés előtti, a vesszősek az ütközés utániakat jelölik, <math>\Omega</math> a relatív sebességek megváltozási szöge, <math>\sigma</math> az ütközési hatáskeresztmetszet. | ||
| + | |||
| + | |||
| + | |||
| + | |||
== Elektromágnesesen kölcsönható soktestrendszerek == | == Elektromágnesesen kölcsönható soktestrendszerek == | ||
A lap 2011. június 10., 16:42-kori változata
Az alábbiakban összefoglaljuk a sok részecskét tartalmazó statisztikus rendszerek leírására szolgáló egyenleteket, továbbá néhány fontos alkalmazást is megemlítünk. Ezekből az egyenleteből származtatható további eredmények pedig a Transzportfolyamatok tételben kerülnek kifejtésre.
Tartalomjegyzék
Soktestrendszerek kontinuum leírása
Amikor nagyon sok részecskének a jellemzőit kell leírni, akkor célszerű mindent eloszlásfüggvényekkel kifejezni. Az eloszlásfüggvény felintegrálva részecskeszámot ad. Meg kell azonban különböztetni, hogy hány részecskére vonatkozik az eloszlásfüggvény. Speciálisan az egyrészecske-eloszlásfüggvény azt mondja meg, hogy mekkra valószínűséggel találunk a 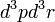 fázistérfogatban 1 részecskét (vagy N-et, a normálás konvenció kérdése), az egyszerűség kedvéért 3 dimenzióra specializálva a tárgyalást:
fázistérfogatban 1 részecskét (vagy N-et, a normálás konvenció kérdése), az egyszerűség kedvéért 3 dimenzióra specializálva a tárgyalást:
Ezzel szemben az általános N részecske-eloszlásfüggvény:
A Liouville-egyenlet
Az eloszlásfüggvények megváltozásának leírásához valamilyen mozgásegyenletre van szükségünk. A legegyszerűbb és egyben legáltalánosabb ilyen egyenlet a Liouville-egyenlet, amely az N részecske-eloszlásfüggvényre vonatkozik:
Itt 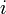 indexeli az
indexeli az 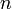 darab részecskét,
darab részecskét, 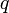 a kanonikus koordináta,
a kanonikus koordináta, 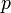 a konjugált impulzus és az időderiváltakat a szokásos módon a Hamilton operátor adja:
a konjugált impulzus és az időderiváltakat a szokásos módon a Hamilton operátor adja:
Fontos kiemelni, hogy a Liouville-egyenlet egy 6n dimenziós egyenlet (szemben a későbbiekkel). Tömören megfogalmazva a fázistérfogat megmaradását fejezi ki a mozgás trajektóriája mentén. Speciálisan 1 klasszikus részecskére az egyenlet:
A Boltzmann-egyenlet
A Boltzmann-egyenlet Boltzmann-egyenlet az előzőekkel szemben az egyrészecske-eloszlásfüggvényre vonatkozó mozgásegyenletet adja meg. Alapvetően ez is a fázistérfogat megmaradására épít, amely külső erőhatás esetén ütközések nélkül:
A jobboldal az eloszlásfüggvény teljes deriváltja ha 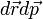 infinitezimális. Ha ütközések is vannak, azok a jobboldalra írhatóak. Ezekkel együtt a Boltzmann-egyenlet:
infinitezimális. Ha ütközések is vannak, azok a jobboldalra írhatóak. Ezekkel együtt a Boltzmann-egyenlet:
Azaz az ütközési tagtól eltekintve visszakaptuk a Liouville-egyenlet fenti speciális esetét. Boltzmann nagy eredménye az volt, hogy az ütközési tagra is tudott jól használható feltevést tenni az egyrészecske-eloszlásfüggvényekkel kifejezve. Ez a molekuláris káosz feltevés, amely arra épül, hogy a részecskék sebességei korrelálatlanok az ütközés előtt és után, továbbá függetlenek a helytől. Ennek a segítségével az ütközési tag:
ahol az 1, 2 indexek az egyik és másik részecske adatait indexelik, a vesszőtlen menyiségek az ütközés előtti, a vesszősek az ütközés utániakat jelölik, 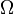 a relatív sebességek megváltozási szöge,
a relatív sebességek megváltozási szöge, 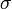 az ütközési hatáskeresztmetszet.
az ütközési hatáskeresztmetszet.