„Dinamikai rendszerek, kaotikus viselkedés” változatai közötti eltérés
| 21. sor: | 21. sor: | ||
A valós folyamatok leírásában (egyszerű rendszerekre, pl.: kettős inga) fel tudjuk írni a rendszert mozgató differenciálegyenleteket, viszont a kezdőfeltételeket csak valamekkora hibával ismerjük. Mivel a kaotikus mozgás hibaerősítő, a mozgást a rövid előrejelzési időn túl követve a bizonytalanság eléri az egész attraktor méretét. Az ilyen mozgás tehát előre jelezhetetlen,rendszerint a fázistér fraktálalakzataihoz kötött, és hosszú távú leírása egy időfüggetlen valószínűségeloszlással lehetséges. | A valós folyamatok leírásában (egyszerű rendszerekre, pl.: kettős inga) fel tudjuk írni a rendszert mozgató differenciálegyenleteket, viszont a kezdőfeltételeket csak valamekkora hibával ismerjük. Mivel a kaotikus mozgás hibaerősítő, a mozgást a rövid előrejelzési időn túl követve a bizonytalanság eléri az egész attraktor méretét. Az ilyen mozgás tehát előre jelezhetetlen,rendszerint a fázistér fraktálalakzataihoz kötött, és hosszú távú leírása egy időfüggetlen valószínűségeloszlással lehetséges. | ||
| − | A legismertebb példája a determinisztikus káosznak a logisztikus leképzés. Ezt nem differenciálegyenlettel írjuk le, hanem a másik lehetséges módon, leképezés formában, ami a következő: <math>x_{n+1} = r\,x_n(1-x_n)</math>. Az x változó a [0:1] tartományon értelmezhető, az r paraméter pedig [0:4] lehet. A leképezést populációdinamikai modellekben szokták használni, ahol x a populáció hányada a teljes lehetséges populációhoz, az r pedig a szaporodási és a pusztulási ráta kombinációja. | + | A legismertebb példája a determinisztikus káosznak a logisztikus leképzés. Ezt nem differenciálegyenlettel írjuk le, hanem a másik lehetséges módon, leképezés formában, ami a következő: <math>x_{n+1} = r\,x_n(1-x_n)</math>. Az x változó a [0:1] tartományon értelmezhető, az r paraméter pedig [0:4] lehet. A leképezést populációdinamikai modellekben szokták használni, ahol x a populáció hányada a teljes lehetséges populációhoz, az r pedig a szaporodási és a pusztulási ráta kombinációja. Az x<sub>n</sub> sorozat viselkedését az r paraméter határozza meg. Ha r<3, akkor 1 fixpont van, ha 3<r<3.4, akkor 2 fixpont van, stb. Hogy melyik r értéknél milyen viselkedést tapasztalunk, a [http://en.wikipedia.org/wiki/File:LogisticMap_BifurcationDiagram.png bifurkációs diagramról] olvashatjuk le. Még több a logisztikus leképezésről [http://en.wikipedia.org/wiki/Logistic_map itt]. |
| − | < | ||
== Káosz disszipatív rendszerekben == | == Káosz disszipatív rendszerekben == | ||
| + | Disszipatív rendszerről akkor beszélünk, amikor a rendszer energiája súrlódás hatására folyamatosan csökken. Ha nem tudjuk a rendszerünket egy mechanikai rendszernek megfeleltetni, akkoronnan vehetjük észre a disszipációt, hogy a fázistérben a fázistérfogat csökken (nullához tart). Az egyik legegyszerűbb példa disszipatív rendszerre a súrlódásos matematikai inga: | ||
| + | |||
| + | <math>\ddot{\Phi} + \gamma \dot{\Phi} + \omega_0^2 sin \Phi = 0</math> | ||
| + | |||
| + | Az egyenletet fel lehet írni két elsőrendű, csatolt differenciálegyenletbe az <math>x = \Phi</math> és az <math>y = \dot{\Phi}</math> helyettesítéssel: | ||
| + | |||
| + | <math>\dot{x} = y</math> | ||
| + | |||
| + | <math>\dot{y} = -\gamma y - \omega_0^2 sin x</math> | ||
| + | |||
| + | A fázistérfogat változását az alábbi egyenlet határozza meg: | ||
| + | |||
| + | <math>\frac{\Delta\dot{V}}{\Delta x \Delta y} = \frac{\Delta \dot{x}}{\Delta x} + \frac{\Delta \dot{y}}{\Delta y} = \vec{\nabla} \cdot \dot{\vec{x}}</math> | ||
| + | |||
| + | A disszipációt tehát úgy is megfogalmazhatjuk, hogy <math>\vec{\nabla} \cdot \dot{\vec{x}} < 0</math> | ||
| + | |||
== Diffúzió == | == Diffúzió == | ||
| − | + | <!--A determinisztikus diffúziót elő lehet állítani az alábbi módon (ugyanazt a leképezést egy egyenesre rakjuk egymás után): | |
| + | |||
| + | [[Fájl:Det_diffusion.png|700px]]--> | ||
| + | |||
| + | A determinisztikus diffúziót megfigyelhetjük a lökdösött rotátoron. Ez egy olyan rotátor, ami T időnként hirtelen impulzust kap (a lökés amplitúdója általában a hely periodikus függvénye, pl.: f(x) = a*sin x). A lökések amplitúdója bármilyen értéket felvehet a (-a,a) intervallumban, a sebesség változás ezért véletlen bolyongásnak fog megfelelni (<math>v_{n+1} = v_n +a sin(x_{n+1})\,</math>, ezért <math>-\infty < v_n < \infty</math>). A sebességtengely 2<math>\pi</math> hosszúságú intervallumán nagy számú pontot indítva azt tapasztaljuk, hogy azok a v<sub>n</sub> tengely mentén egyre jobban szétterjednek. A kaotikus dinamika tehát egy diffúziós folyamatot hozott létre. | ||
| + | |||
| + | A bolyongás során egy részecske koordinátája az i-edik lépésben éppen <math>r_i = a\,sin(x_{i+1})</math>-gyel változik meg. Ha r<sub>i</sub>-k függetlennek tekinthetők, akkor az átlag elmozdulás <math>\bar{R_n} = \bar{\Sigma r_i} = 0</math>, a négyzetes átlagos elmozdulás pedig <math>\bar{R_n^2}</math>. A függetlenség miatt igaz, hogy <math>\bar{R_n^2} = \bar{r_i^2}n</math>. A bolyongás diffúziós együtthatóját a <math>\bar{R_n^2} = 2Dn</math> képletből kifejezhetjük: <math>D = \bar{r_i^2}/2</math>. Behelyettesítve r<sub>i</sub> értékét: <math>D = \frac{1}{4}a^2</math>. | ||
| + | |||
| + | Mindebből tehát azt szűrhetjük le, hogy a determinisztikus eredetű mozgás elegendően hosszú idő alatt pont olyan folyamatot képes létrehozni, mint valamilyen külső zaj. Ez annak a megnyilvánulása, hogy a káosz véletlenszerű mozgást jelent, és ez jól definiált valószínűség-eloszlással jellemezhető. A diffúzió tehát arra ''nem'' érzékeny, hogy a bolyongást kiváltó hatás milyen eredetű. | ||
| + | |||
== Zaj dominált rendszerek == | == Zaj dominált rendszerek == | ||
A lap 2011. június 10., 23:22-kori változata
Tartalomjegyzék
Dinamikai rendszerek elmélete
A dinamikai rendszerek elmélete csatolt differenciálegyenletek tulajdonságával foglalkozik, amiknek az időfejlődését néhány paraméter határozza meg. A rendszer időfejlődésének vizsgálata a paraméterek állapotterében zajlik.
Alapfogalmak
Fixpont és határciklus
Fixpontnak azt nevezzük, amikor a rendszer hosszú idő után a fázistér egy pontjában található meg. A fixpont lehet stabil (kis kitérésre visszatér), és instabil (kis kitérésre nem tér vissza). A határciklus a fázistérben egy zárt trajektória, amin a rendszer az idő előrehaladtával körbejár. Szintén lehet stabil vagy instabil.
Bifurkáció
Bifurkációról akkor beszélünk, amikor egy külső paraméter hatására a rendszer hosszú távú viselkedése kvalitatívan megváltozik (pl.: 1 fixpont → 2 fixpont, fixpont → határciklus, stb.)
Poincaré-metszet
A rendszer időfejlődését, főleg ha az d>3 dimenziós, nagyon nehéz grafikusan ábrázolni. Ezért a fázistérnek és egy síknak a metszetét vizsgáljuk. Ha egy közel periodikus pálya metszi a síkot (a fázistér egy alterét), akkor egy periódusidő múlva újra metszeni fogja, közel az előző ponthoz. Belátható, hogy egy pálya akkor periodikus, ha a Poincaré-metszetnek fixpontja.
Ljapunov-exponens
A Ljapunov-exponenssel az számszerűsíthetjük, hogy a fázistérben két közeli trajektória milyen gyorsan távolodik egymástól. Ha kezdetben 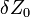 távolságra voltak, akkor az időben a távolságuk
távolságra voltak, akkor az időben a távolságuk 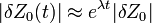 szerint növekszik.
szerint növekszik.
Attraktor
A fázistér vonzó halmaza, vagyis olyan halmaza, amely felé a trajektóriák közelednek. Disszipatív rendszerekben fordulnak elő, fázistérfogatuk zérus.
Determinisztikus káosz
Az egyszerű, kevés összetevőből álló rendszerek szabálytalan mozgását kaotikusnak nevezzük. Jellemzői:
- nem ismétli önmagát
- nem jelezhető előre, mert érzékeny a kezdőfeltételekre, melyeket véges pontossággal ismerünk
- a visszatérési szabály bonyolult geometriájú (pl.: hely-sebesség ábrázolásban egy komplex, de szabályos szerkezet jelenik meg)
A valós folyamatok leírásában (egyszerű rendszerekre, pl.: kettős inga) fel tudjuk írni a rendszert mozgató differenciálegyenleteket, viszont a kezdőfeltételeket csak valamekkora hibával ismerjük. Mivel a kaotikus mozgás hibaerősítő, a mozgást a rövid előrejelzési időn túl követve a bizonytalanság eléri az egész attraktor méretét. Az ilyen mozgás tehát előre jelezhetetlen,rendszerint a fázistér fraktálalakzataihoz kötött, és hosszú távú leírása egy időfüggetlen valószínűségeloszlással lehetséges.
A legismertebb példája a determinisztikus káosznak a logisztikus leképzés. Ezt nem differenciálegyenlettel írjuk le, hanem a másik lehetséges módon, leképezés formában, ami a következő: 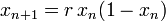 . Az x változó a [0:1] tartományon értelmezhető, az r paraméter pedig [0:4] lehet. A leképezést populációdinamikai modellekben szokták használni, ahol x a populáció hányada a teljes lehetséges populációhoz, az r pedig a szaporodási és a pusztulási ráta kombinációja. Az xn sorozat viselkedését az r paraméter határozza meg. Ha r<3, akkor 1 fixpont van, ha 3<r<3.4, akkor 2 fixpont van, stb. Hogy melyik r értéknél milyen viselkedést tapasztalunk, a bifurkációs diagramról olvashatjuk le. Még több a logisztikus leképezésről itt.
. Az x változó a [0:1] tartományon értelmezhető, az r paraméter pedig [0:4] lehet. A leképezést populációdinamikai modellekben szokták használni, ahol x a populáció hányada a teljes lehetséges populációhoz, az r pedig a szaporodási és a pusztulási ráta kombinációja. Az xn sorozat viselkedését az r paraméter határozza meg. Ha r<3, akkor 1 fixpont van, ha 3<r<3.4, akkor 2 fixpont van, stb. Hogy melyik r értéknél milyen viselkedést tapasztalunk, a bifurkációs diagramról olvashatjuk le. Még több a logisztikus leképezésről itt.
Káosz disszipatív rendszerekben
Disszipatív rendszerről akkor beszélünk, amikor a rendszer energiája súrlódás hatására folyamatosan csökken. Ha nem tudjuk a rendszerünket egy mechanikai rendszernek megfeleltetni, akkoronnan vehetjük észre a disszipációt, hogy a fázistérben a fázistérfogat csökken (nullához tart). Az egyik legegyszerűbb példa disszipatív rendszerre a súrlódásos matematikai inga:
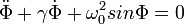
Az egyenletet fel lehet írni két elsőrendű, csatolt differenciálegyenletbe az 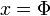 és az
és az 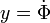 helyettesítéssel:
helyettesítéssel:
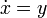
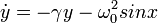
A fázistérfogat változását az alábbi egyenlet határozza meg:
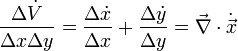
A disszipációt tehát úgy is megfogalmazhatjuk, hogy 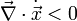
Diffúzió
A determinisztikus diffúziót megfigyelhetjük a lökdösött rotátoron. Ez egy olyan rotátor, ami T időnként hirtelen impulzust kap (a lökés amplitúdója általában a hely periodikus függvénye, pl.: f(x) = a*sin x). A lökések amplitúdója bármilyen értéket felvehet a (-a,a) intervallumban, a sebesség változás ezért véletlen bolyongásnak fog megfelelni (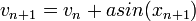 , ezért
, ezért 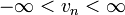 ). A sebességtengely 2
). A sebességtengely 2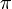 hosszúságú intervallumán nagy számú pontot indítva azt tapasztaljuk, hogy azok a vn tengely mentén egyre jobban szétterjednek. A kaotikus dinamika tehát egy diffúziós folyamatot hozott létre.
hosszúságú intervallumán nagy számú pontot indítva azt tapasztaljuk, hogy azok a vn tengely mentén egyre jobban szétterjednek. A kaotikus dinamika tehát egy diffúziós folyamatot hozott létre.
A bolyongás során egy részecske koordinátája az i-edik lépésben éppen 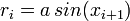 -gyel változik meg. Ha ri-k függetlennek tekinthetők, akkor az átlag elmozdulás
-gyel változik meg. Ha ri-k függetlennek tekinthetők, akkor az átlag elmozdulás 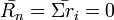 , a négyzetes átlagos elmozdulás pedig
, a négyzetes átlagos elmozdulás pedig 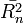 . A függetlenség miatt igaz, hogy
. A függetlenség miatt igaz, hogy 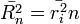 . A bolyongás diffúziós együtthatóját a
. A bolyongás diffúziós együtthatóját a 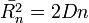 képletből kifejezhetjük:
képletből kifejezhetjük: 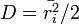 . Behelyettesítve ri értékét:
. Behelyettesítve ri értékét: 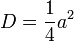 .
.
Mindebből tehát azt szűrhetjük le, hogy a determinisztikus eredetű mozgás elegendően hosszú idő alatt pont olyan folyamatot képes létrehozni, mint valamilyen külső zaj. Ez annak a megnyilvánulása, hogy a káosz véletlenszerű mozgást jelent, és ez jól definiált valószínűség-eloszlással jellemezhető. A diffúzió tehát arra nem érzékeny, hogy a bolyongást kiváltó hatás milyen eredetű.