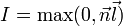„Vizualizációs módszerek” változatai közötti eltérés
a |
(→Képalkotó módszerek) |
||
| 1. sor: | 1. sor: | ||
== Képalkotó módszerek == | == Képalkotó módszerek == | ||
| + | Ha 3D-s objektumokat szeretnénk megjeleníteni, valamennyire is kötődve a valóságos fényviszonyok reprodukálására, akkor alapvetően két fajta megközelítésből kell választanunk. Az egyik a fizikailag intuitív sugárkövetés alapú módszerek családja. Itt lényegében az intenzitást sugarak terjesztik az objektumok, így például a képernyőt reprezentáló kamera felületei között. A másik módszer, a raszterizáció eleve kihasználja, hogy a képet diszkrét pixelekből álló 2D-s rácson akarjuk előállítani és a problémát lényegében a felületek vetületeinek kitöltésére transzformálja. | ||
| + | |||
=== Raszterizáció === | === Raszterizáció === | ||
| + | Legyenek adottak a felületek, amelyeket le szeretnénk rajzolni a képernyőre. Ez nyilvánvalóan tartalmaz egy vetítést a 3D-s térből a 2D-s képfelületre. Ezt a lépést a raszterizáció a felületek (tipikusan poligonok) analitikus transzformációjával állítja elő. Poligonok esetén ez a csúcspontok levetítését jelenti. Ezek után két feladat van: előállítani pixelere diszkretizált képfelületen az alakzat körvonalát, majd kitölteni azt. | ||
| + | |||
| + | Négyzetrácsos képsík esetén mindkét feladat igen hatkékony algoritmusokkal valósítható meg. Az alakzat körvonalának előállítására a legegyszerűbb módszer a Bresemham-approximáció. Ez megadott két pont között sorban bejárja azokat a pixeleket, amelyeken a vonal áthalad. Az eljárás lényege, hogy a kindulási pontnak megfelelő pixelnél inicializál egy hiba változót, amit az egyenes meredekségének megfelelő értékkel növel. Amikor ez a hiba eléri azt a küszöböt, amikor az egyenes már a másik pixelhez van közelebb, akkor eggyel növeli az aktuális koordinátát és csökkenti a hibát. Az eljárás előnye, hogy lebegőpontos műveletek nélkül mnegvalósítható, olyan hatékonyan, hogy a belső ciklus léptetése csupűán néhány órajelet igényel. | ||
| + | |||
| + | Az alakzat körvonala után annak kitöltése úgy történhet, hogy meghatározzuk körvonal befoglaló téglalapját, és minden sorban a befoglaló széléről elindulva megnézzük, hogy mikor érünk el a körvonalhoz tartozó (előre megjelölt) pixelt. Ekkortól minden pixelt kitöltünk addig, amíg újra egy eleve már megjelölt pixelhez nem értünk. | ||
| + | |||
| + | A raszterizációs módszerek valóságot imitáló trükkjei ott jelennek meg, hogy milyen színértékeket rendelünk a kitöltés során a pixelekhez. Mivel poligonjaink vannak, ezek mindig háromszögekre bonthatóak (sőt, eleve így vannak tárolva). Minden a fényhatásokat jellemző paramétert a háromszögek csúcsaiban szokás eltárolni (a pozíción túl a felületi normális, adott pont beli szín, felületi textúra koordináta stb.), majd ezeket az értékeket interpolálni a háromszög felületén az aktuális kitöltési pontokra. | ||
| + | |||
| + | Igen egyszerű példaként, tekintsük a legegyszerűbb megvilágítást: ha egy háromszög a pontszerű fényforrás felé néz, akkor világosabb, ha elfele, akkor sötétebb. A legegyszerűbb esetben ezt a fényforrás irányának (l) és a felületi normálisnak (n) az irányával lehet elérni, Így az adott pixel intenzitás értéke a két normálvektor skalárisszorzata: | ||
| + | |||
| + | :<math>I = \mathrm{max}(0, \vec{n}\vec{l})</math> | ||
| + | |||
| + | ahol a skalárisszorzat negatív lenne, ott zérus lesz a megvilágítás és így az intenzitás is. | ||
| + | |||
=== Sugárkövetés === | === Sugárkövetés === | ||
| + | |||
== Szín-rendszerek == | == Szín-rendszerek == | ||
{{MSc záróvizsga}} | {{MSc záróvizsga}} | ||
A lap 2011. június 11., 19:04-kori változata
Tartalomjegyzék
Képalkotó módszerek
Ha 3D-s objektumokat szeretnénk megjeleníteni, valamennyire is kötődve a valóságos fényviszonyok reprodukálására, akkor alapvetően két fajta megközelítésből kell választanunk. Az egyik a fizikailag intuitív sugárkövetés alapú módszerek családja. Itt lényegében az intenzitást sugarak terjesztik az objektumok, így például a képernyőt reprezentáló kamera felületei között. A másik módszer, a raszterizáció eleve kihasználja, hogy a képet diszkrét pixelekből álló 2D-s rácson akarjuk előállítani és a problémát lényegében a felületek vetületeinek kitöltésére transzformálja.
Raszterizáció
Legyenek adottak a felületek, amelyeket le szeretnénk rajzolni a képernyőre. Ez nyilvánvalóan tartalmaz egy vetítést a 3D-s térből a 2D-s képfelületre. Ezt a lépést a raszterizáció a felületek (tipikusan poligonok) analitikus transzformációjával állítja elő. Poligonok esetén ez a csúcspontok levetítését jelenti. Ezek után két feladat van: előállítani pixelere diszkretizált képfelületen az alakzat körvonalát, majd kitölteni azt.
Négyzetrácsos képsík esetén mindkét feladat igen hatkékony algoritmusokkal valósítható meg. Az alakzat körvonalának előállítására a legegyszerűbb módszer a Bresemham-approximáció. Ez megadott két pont között sorban bejárja azokat a pixeleket, amelyeken a vonal áthalad. Az eljárás lényege, hogy a kindulási pontnak megfelelő pixelnél inicializál egy hiba változót, amit az egyenes meredekségének megfelelő értékkel növel. Amikor ez a hiba eléri azt a küszöböt, amikor az egyenes már a másik pixelhez van közelebb, akkor eggyel növeli az aktuális koordinátát és csökkenti a hibát. Az eljárás előnye, hogy lebegőpontos műveletek nélkül mnegvalósítható, olyan hatékonyan, hogy a belső ciklus léptetése csupűán néhány órajelet igényel.
Az alakzat körvonala után annak kitöltése úgy történhet, hogy meghatározzuk körvonal befoglaló téglalapját, és minden sorban a befoglaló széléről elindulva megnézzük, hogy mikor érünk el a körvonalhoz tartozó (előre megjelölt) pixelt. Ekkortól minden pixelt kitöltünk addig, amíg újra egy eleve már megjelölt pixelhez nem értünk.
A raszterizációs módszerek valóságot imitáló trükkjei ott jelennek meg, hogy milyen színértékeket rendelünk a kitöltés során a pixelekhez. Mivel poligonjaink vannak, ezek mindig háromszögekre bonthatóak (sőt, eleve így vannak tárolva). Minden a fényhatásokat jellemző paramétert a háromszögek csúcsaiban szokás eltárolni (a pozíción túl a felületi normális, adott pont beli szín, felületi textúra koordináta stb.), majd ezeket az értékeket interpolálni a háromszög felületén az aktuális kitöltési pontokra.
Igen egyszerű példaként, tekintsük a legegyszerűbb megvilágítást: ha egy háromszög a pontszerű fényforrás felé néz, akkor világosabb, ha elfele, akkor sötétebb. A legegyszerűbb esetben ezt a fényforrás irányának (l) és a felületi normálisnak (n) az irányával lehet elérni, Így az adott pixel intenzitás értéke a két normálvektor skalárisszorzata:
ahol a skalárisszorzat negatív lenne, ott zérus lesz a megvilágítás és így az intenzitás is.