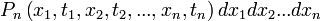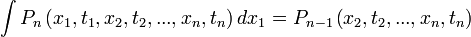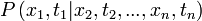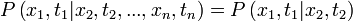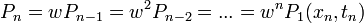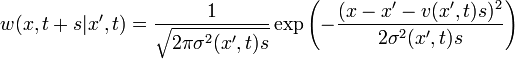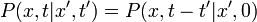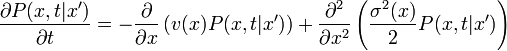„Sztochasztikus folyamatok” változatai közötti eltérés
a |
|||
| 1. sor: | 1. sor: | ||
| + | Az alábbiakban néhány véletlenszerű folyamatot és ezek leírási módszereit tárgyaljuk. | ||
| + | |||
== Kauffman-hálózat == | == Kauffman-hálózat == | ||
== Spinüvegek == | == Spinüvegek == | ||
Valakinek bármi ötléete, hogy ez hogy jön ide??? | Valakinek bármi ötléete, hogy ez hogy jön ide??? | ||
== Markov-lánc, Markov-folyamatok == | == Markov-lánc, Markov-folyamatok == | ||
| + | Egy sztochasztikus folyamatot jellemezhetünk azzal, hogy diszkrét időpillanatokban a tekintett valószínűségi változó milyen értékeket vett fel. Egy rendszert akkor tekintünk leírtnak, ha meg tudjuk mondani minden időpillanatra, minden értékre a megfelelő valószínűségeket: | ||
| + | |||
| + | :<math>P_n\left(x_1, t_1, x_2, t_2, ..., x_n, t_n\right)dx_1 dx_2 ... dx_n</math> | ||
| + | |||
| + | ahol <math>n</math> a leírni kívánt lépések száma. Mivel ez egy valószínűség, ezért minden <math>x</math> változójára kiintegrálva 1-et kell kapnunk, ez a norma-feltétel. Ezen felül, ha csak egy x változóra integrálunk, akkor az eggyel kisebb "rendű" valószínűségi kifejezést kell kapnunk: | ||
| + | |||
| + | :<math>\int P_n\left(x_1, t_1, x_2, t_2, ..., x_n, t_n\right)dx_1 = P_{n-1}\left(x_2, t_2, ..., x_n, t_n\right)</math> | ||
| + | |||
| + | Tehát ha az egyik mintavételi időpontban minden lehetséges kimenetelre integrálunk, akkor olyan, mintha azt a pontot nem vennénk figyelembe. Ez a kompatibilitási feltétel. | ||
| + | |||
| + | Markov-folyamatoknál a rendszer jövőbeli állapotainak valószínűségét a korábbi, ismert állapotokból szeretnénk meghatározni. Ennek megfelelően ezt egy feltételes valószínűséggel fogalmazhatjuk meg: | ||
| + | |||
| + | :<math>P\left(x_1, t_1|x_2, t_2, ..., x_n, t_n\right)</math> | ||
| + | |||
| + | azaz, ha ismert a rendszer vislkedése <math>t_2, ...., t_n</math> pillanatokban, akkor emellett a feltétel mellett milyen valószínűséggel lesz <math>t_1</math>-ben <math>x_1</math> állapotban. Egy folyamat akkor Markov-folyamat, ha rendelkezik a Markov-tulajdonsággal, ami azt mondja, hogy a rendszer csak a legutóbbi állpotától függ: | ||
| + | |||
| + | :<math>P\left(x_1, t_1|x_2, t_2, ..., x_n, t_n\right) = P\left(x_1, t_1|x_2, t_2\right)</math> | ||
| + | |||
| + | Ebből következik, hogyha 1 pontban ismert a Markov-folyamat, valamint az átmeneti valószínűségek, akkor teljes rendszer ismert, mert rekurzívan minden következő (vagy megelőző) állapot felírható az átmeneti valószínűségekkel: | ||
| + | |||
| + | :<math>P_n = w P_{n-1} = w^2 P_{n-2} = ... = w^n P_1(x_n, t_n)\,</math> | ||
| + | |||
| + | Például ha egy diffúziós-folyamatot szeretnénk leírni, akkor az átmeneti valószínűség Gauss: | ||
| + | :<math>w(x, t+s|x', t) = \frac{1}{\sqrt{2\pi \sigma^2(x', t) s}} \exp\left(-\frac{(x-x'-v(x', t)s)^2}{2\sigma^2(x', t)s}\right)\,</math> | ||
| + | |||
| + | Homogénnek nevezzük a Markov-folyamatot, ha az átmeneti valószínűég időeltolás-invariáns: | ||
| + | :<math>P(x, t|x', t') = P(x, t-t'|x', 0)\,</math> | ||
| + | |||
| + | Homogén diffúziós folyamatokra eben a kontextusban is levezethető a Fokker-Planck-egyenlet, ami lényegében a valószínűség-áramsűrűség megmaradását fejezi ki: | ||
| + | |||
| + | :<math>\frac{\partial P(x, t|x')}{\partial t} = -\frac{\partial}{\partial x}\left( v(x)P(x, t|x') \right) + \frac{\partial^2}{\partial x^2}\left( \frac{\sigma^2(x)}{2}P(x, t|x') \right)\,</math> | ||
{{MSc záróvizsga}} | {{MSc záróvizsga}} | ||
A lap 2011. június 12., 10:57-kori változata
Az alábbiakban néhány véletlenszerű folyamatot és ezek leírási módszereit tárgyaljuk.
Kauffman-hálózat
Spinüvegek
Valakinek bármi ötléete, hogy ez hogy jön ide???
Markov-lánc, Markov-folyamatok
Egy sztochasztikus folyamatot jellemezhetünk azzal, hogy diszkrét időpillanatokban a tekintett valószínűségi változó milyen értékeket vett fel. Egy rendszert akkor tekintünk leírtnak, ha meg tudjuk mondani minden időpillanatra, minden értékre a megfelelő valószínűségeket:
ahol 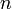 a leírni kívánt lépések száma. Mivel ez egy valószínűség, ezért minden
a leírni kívánt lépések száma. Mivel ez egy valószínűség, ezért minden 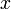 változójára kiintegrálva 1-et kell kapnunk, ez a norma-feltétel. Ezen felül, ha csak egy x változóra integrálunk, akkor az eggyel kisebb "rendű" valószínűségi kifejezést kell kapnunk:
változójára kiintegrálva 1-et kell kapnunk, ez a norma-feltétel. Ezen felül, ha csak egy x változóra integrálunk, akkor az eggyel kisebb "rendű" valószínűségi kifejezést kell kapnunk:
Tehát ha az egyik mintavételi időpontban minden lehetséges kimenetelre integrálunk, akkor olyan, mintha azt a pontot nem vennénk figyelembe. Ez a kompatibilitási feltétel.
Markov-folyamatoknál a rendszer jövőbeli állapotainak valószínűségét a korábbi, ismert állapotokból szeretnénk meghatározni. Ennek megfelelően ezt egy feltételes valószínűséggel fogalmazhatjuk meg:
azaz, ha ismert a rendszer vislkedése 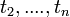 pillanatokban, akkor emellett a feltétel mellett milyen valószínűséggel lesz
pillanatokban, akkor emellett a feltétel mellett milyen valószínűséggel lesz 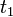 -ben
-ben 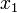 állapotban. Egy folyamat akkor Markov-folyamat, ha rendelkezik a Markov-tulajdonsággal, ami azt mondja, hogy a rendszer csak a legutóbbi állpotától függ:
állapotban. Egy folyamat akkor Markov-folyamat, ha rendelkezik a Markov-tulajdonsággal, ami azt mondja, hogy a rendszer csak a legutóbbi állpotától függ:
Ebből következik, hogyha 1 pontban ismert a Markov-folyamat, valamint az átmeneti valószínűségek, akkor teljes rendszer ismert, mert rekurzívan minden következő (vagy megelőző) állapot felírható az átmeneti valószínűségekkel:
Például ha egy diffúziós-folyamatot szeretnénk leírni, akkor az átmeneti valószínűség Gauss:
Homogénnek nevezzük a Markov-folyamatot, ha az átmeneti valószínűég időeltolás-invariáns:
Homogén diffúziós folyamatokra eben a kontextusban is levezethető a Fokker-Planck-egyenlet, ami lényegében a valószínűség-áramsűrűség megmaradását fejezi ki: