„Soktest rendszerek” változatai közötti eltérés
a (→Relaxációs közelítés az ütközési tagra) |
|||
| (18 közbenső módosítás ugyanattól a szerkesztőtől nincs mutatva) | |||
| 1. sor: | 1. sor: | ||
Az alábbiakban összefoglaljuk a sok részecskét tartalmazó statisztikus rendszerek leírására szolgáló egyenleteket, továbbá néhány fontos alkalmazást is megemlítünk. Ezekből az egyenleteből származtatható további eredmények pedig a [[Transzportfolyamatok]] tételben kerülnek kifejtésre. | Az alábbiakban összefoglaljuk a sok részecskét tartalmazó statisztikus rendszerek leírására szolgáló egyenleteket, továbbá néhány fontos alkalmazást is megemlítünk. Ezekből az egyenleteből származtatható további eredmények pedig a [[Transzportfolyamatok]] tételben kerülnek kifejtésre. | ||
| − | == | + | A sokrészecskés rendszerek leírásának három szintje van. A legalapvetőbb, mikroszkópikus szinten minden részecskét külön kezelünk. Ez a klasszikus esetben minden részecskére egy Newton-egyenlet csatolását jelenti. Egy Avogadro-szám nagyságrendű rendszerre ennek a megoldása lehetetlen. Ilyen esetekben célszerű a kinetikus megközelítésben számolni, ahol az egyrészecske tulajdonságokat statisztikus átalagokkal váltjuk fel, és ezekre az átlagokra írjuk fel az egyenleteket. Itt a változóink még mindig mikroszkópikus mennyiségek, de már jóval kevesebb van belőlük, mint a részecskék száma. A harmadik szint a makroszkópikus tárgyalás, ahol már a makroszkópikus állapotjelzőkre vonatkoznak az egyenletek, mint például hőmérséklet, nyomás stb. Az alábbiakban a kinetikus tárgyalásmóddal foglalkozunk. |
| + | |||
| + | == Klasszikus sokrészecskerendszerek leírása == | ||
Amikor nagyon sok részecskének a jellemzőit kell leírni, akkor célszerű mindent eloszlásfüggvényekkel kifejezni. Az eloszlásfüggvény felintegrálva részecskeszámot ad. Meg kell azonban különböztetni, hogy hány részecskére vonatkozik az eloszlásfüggvény. Speciálisan az egyrészecske-eloszlásfüggvény azt mondja meg, hogy mekkra valószínűséggel találunk a <math>d^3 p d^3 r</math> fázistérfogatban 1 részecskét (vagy N-et, a normálás konvenció kérdése), az egyszerűség kedvéért 3 dimenzióra specializálva a tárgyalást: | Amikor nagyon sok részecskének a jellemzőit kell leírni, akkor célszerű mindent eloszlásfüggvényekkel kifejezni. Az eloszlásfüggvény felintegrálva részecskeszámot ad. Meg kell azonban különböztetni, hogy hány részecskére vonatkozik az eloszlásfüggvény. Speciálisan az egyrészecske-eloszlásfüggvény azt mondja meg, hogy mekkra valószínűséggel találunk a <math>d^3 p d^3 r</math> fázistérfogatban 1 részecskét (vagy N-et, a normálás konvenció kérdése), az egyszerűség kedvéért 3 dimenzióra specializálva a tárgyalást: | ||
:<math>N(t) = \int_{-\infty}^{+\infty} f(\vec{r}, \vec{p}, t) \, d^3 \vec{r} \, d^3 \vec{p}.</math> | :<math>N(t) = \int_{-\infty}^{+\infty} f(\vec{r}, \vec{p}, t) \, d^3 \vec{r} \, d^3 \vec{p}.</math> | ||
| − | Ezzel szemben az általános N részecske-eloszlásfüggvény: | + | Ezzel szemben az általános N részecske-eloszlásfüggvény azt mondja meg, hogy mekkora valószínőséggel találjuk egy időben az első részecskét az 1. fázistér-pontban, a második részecskét a 2. fázistér pontban, ... stb.: |
:<math>N(t) = \int_{-\infty}^{+\infty} d^3 \vec{r}_1 \, d^3 \vec{p}_1 ... \int_{-\infty}^{+\infty} d^3 \vec{r}_N \, d^3 \vec{p}_N f(\vec{r}_1, \vec{p}_1, ..., \vec{r}_N, \vec{p}_N, t) \, .</math> | :<math>N(t) = \int_{-\infty}^{+\infty} d^3 \vec{r}_1 \, d^3 \vec{p}_1 ... \int_{-\infty}^{+\infty} d^3 \vec{r}_N \, d^3 \vec{p}_N f(\vec{r}_1, \vec{p}_1, ..., \vec{r}_N, \vec{p}_N, t) \, .</math> | ||
| 26. sor: | 28. sor: | ||
:<math>\frac{\partial f}{\partial t}+\frac{\vec{p}}{m}\cdot\nabla_\vec{r}f+\vec{F}\cdot \nabla_\vec{p} f=0.</math> | :<math>\frac{\partial f}{\partial t}+\frac{\vec{p}}{m}\cdot\nabla_\vec{r}f+\vec{F}\cdot \nabla_\vec{p} f=0.</math> | ||
| + | |||
| + | === Molekula dinamika === | ||
| + | Nagyon nagy vonalakban csak arról van szó, hogy a Liouville-egyenletet tekintjük úgy, hogy a deriváltakat a Newton-féle erőtörvény adja. | ||
=== A Boltzmann-egyenlet === | === A Boltzmann-egyenlet === | ||
| 34. sor: | 39. sor: | ||
</math> | </math> | ||
| − | A | + | A baloldal az eloszlásfüggvény teljes deriváltja ha <math>d\vec{r} d \vec{p}</math> infinitezimális. Ha ütközések is vannak, azok a jobboldalra írhatóak. Ezekkel együtt a Boltzmann-egyenlet: |
:<math> | :<math> | ||
\frac{\partial f}{\partial t} | \frac{\partial f}{\partial t} | ||
| − | + \frac{\vec{p}}{m} \nabla_\vec{r} | + | + \frac{\vec{p}}{m} \nabla_\vec{r} f |
| − | + \vec{F} \nabla_\vec{p} | + | + \vec{F} \nabla_\vec{p} f |
= \left. \frac{\partial f}{\partial t} \right|_{\mathrm{coll}}. | = \left. \frac{\partial f}{\partial t} \right|_{\mathrm{coll}}. | ||
</math> | </math> | ||
| 46. sor: | 51. sor: | ||
:<math> | :<math> | ||
| − | \left. \frac{\partial f}{\partial t} \right|_{\mathrm{coll}} = \int d\Omega \int \, d\vec{p}_2 \, \sigma(\Omega) \, |\vec{p}_1 - \vec{p}_2| (f'_1 f'_2 - f_1 f_2) | + | \left. \frac{\partial f}{\partial t} \right|_{\mathrm{coll}} = \int d\Omega \int \, d\vec{p}_2 \, \sigma(\Omega) \, \frac{|\vec{p}_1 - \vec{p}_2|}{m} (f'_1 f'_2 - f_1 f_2) |
</math> | </math> | ||
ahol az 1, 2 indexek az egyik és másik részecske adatait indexelik, a vesszőtlen menyiségek az ütközés előtti, a vesszősek az ütközés utániakat jelölik, <math>\Omega</math> a relatív sebességek megváltozási szöge, <math>\sigma</math> az ütközési hatáskeresztmetszet. | ahol az 1, 2 indexek az egyik és másik részecske adatait indexelik, a vesszőtlen menyiségek az ütközés előtti, a vesszősek az ütközés utániakat jelölik, <math>\Omega</math> a relatív sebességek megváltozási szöge, <math>\sigma</math> az ütközési hatáskeresztmetszet. | ||
| + | ==== Relaxációs közelítés az ütközési tagra ==== | ||
| + | Az egyik leggyakrabban használt és legegyszerűbb közelítés a Boltzmnn-egyenlet ütközési tagjára, az úgynevzett relaxációs idő közelítés. Ez akkor igaz, ha igen közel vagyunk az egyensúlyi eloszláshoz, 1 valószínűséggel találhatunk betöltetlen állapotokat (az 1-f jellegű tagokat 1-el közelíthetjük), továbbá az ütközés előtti és utáni állapotokra teljesül a részletes egyensúly elve. Ekkor: | ||
| + | |||
| + | :<math>\left. \frac{\partial f}{\partial t} \right|_{\mathrm{coll}} = -\frac{f - f_0}{\tau(\vec{p}) }</math> | ||
| + | |||
| + | ahol <math>f_0</math> az egyensúlyi eloszlás Fermi-Dirac statisztika esetén: | ||
| + | |||
| + | :<math>f_0(\vec{r}, \vec{p}) = \frac{1}{ \exp\left( \frac{(E(\vec{p}) - E_F)}{kT}\right) + 1 }</math> | ||
| + | |||
| + | Ha eltekintünk a sűrűség gradiensektől és a külső erőhatásoktól, akkor egyszerűen megoldható a Boltzmann-egyenlet: | ||
| + | |||
| + | :<math>f(\vec{r}, \vec{p}, t) = f_0(\vec{r}, \vec{p}) \times \left( 1-\exp\left(- \frac{t}{\tau(\vec{p})}\right)\right) </math> | ||
| + | |||
| + | === A Vlasov-egyenlet === | ||
| + | Vlasov szerint a Boltzmann-féle kinetikus leírás nem jó hosszútávú kölcsönhatásokkal csatolt sokrészecskerendszerek leírására (ő az elektromos plazma leírására használta, de nyilván a gravitáció is hasonló problémákat vet fel). Egyrészt eleoktronszórásos kísérletekkel való ellentmondás, másrészt a plazmaoszcillációkkal való ellentmondás, harmadrészt a kinetikus tagok divergenciái miatt fellépő problémák miatt egy másik kinetikus leírást keresett, amely a Boltzmann-egyenletek és a Maxwell-egyenletek csatolásával leírná az elektronok és a pozitív töltés atomtörzsek egymásrahatását. | ||
| + | |||
| + | Bár az irodalom erősen keveri az elnevezéseket, de úgy fest, hogy a [http://en.wikipedia.org/wiki/Vlasov_equation Vlasov-egyenlet] nem más, mint a Boltzmann-egyenlet ütközési tag nélkül, és az erőhatás az elektromágneses hatásokból származik, csatolva a Maxwell-egyenletekkel: | ||
| + | |||
| + | :<math>\frac{\partial f_{\pm}}{\partial t} + \frac{\vec{p}}{m_{\pm}} \cdot \nabla_{\vec{r}} f_{\pm} \pm e\Bigl(\vec{E}+\frac{1}{c}(\vec{v}\times\vec{B})\Bigr)\cdot \nabla_{\vec{p}} f_{\pm} = 0 | ||
| + | </math> | ||
| + | |||
| + | :<math> | ||
| + | \nabla\times\vec{B}=\frac{4\pi\vec{j}}{c}+\frac{1}{c}\frac{\partial\vec{E}}{\partial t},\quad \nabla\times\vec{E}=-\frac{1}{c}\frac{\partial\vec{B}}{\partial t} | ||
| + | </math> | ||
| + | :<math> | ||
| + | \nabla\cdot\vec{E}=4\pi\rho,\quad \nabla\cdot\vec{B}=0 | ||
| + | </math> | ||
| + | :<math> | ||
| + | \rho=e\int(f_+-f_-)d^3\vec{p},\quad \vec{j}=e\int(f_+-f_-)\vec{v}d^3\vec{p} | ||
| + | </math> | ||
| + | |||
| + | Itt "+" a pozitív töltésű, "-" a negatív töltésű részecskék paramétereit indexeli. Fontos látni, hogy az elektromágneses tér forrásául nem az egyes részecskék, hanem a kiátlagolt eloszlásfüggvények szolgálnak. | ||
| + | |||
| + | == Kvantumos sokrészecskerendszerek leírása == | ||
| + | Legegyszerűbb (nem-relativisztikus) esetben az időfüggő Schrödinger-egyenletet kellene megoldani: | ||
| + | |||
| + | :<math>i \hbar \frac{\partial \Psi}{\partial t} = \mathcal{H} \Psi </math> | ||
| + | |||
| + | ahol <math>\Psi = \Psi(1, 2, ..., N, t)</math> az N-részecske hullámfüggvény, <math>\mathcal{H}</math> pedig a sokrészecske Hamilton-operátor. Ennek precíz megoldása szintén esélytelen. | ||
| + | |||
| + | === A Hartree-Fock módszer === | ||
| + | Statikus esetben egy jó közelítés a [http://en.wikipedia.org/wiki/Hartree-Fock_method Hartree-Fock módszer]. Közelítsük a sokrészecske-hullámfüggvényt egyrészecske-hullámfüggvények kombinációjaként, számoljuk ki a kölcsönhatások átlagait ezekkel, majd oldjuk meg ezekre egyenként az egyrészecske-egyenleteket. Az így kapott új hullámfüggvényekkel újrakezdhető az iteráció, és egy önkonzisztens módszert kaphatunk. | ||
| + | |||
| + | A Hartree és a Hartree-Fock módszer abban különbözik, hogy milyen módon bontják fel a sokrészecske-hullámfüggvényt. Előbbi simán szorzatalakban, utóbbi Slater-determináns alakban teszi ezt, ez nyilván jobb felírás (fermionokra), mert figyelembe veszi a hullámfüggvény antiszimmetrikusságát. | ||
| + | |||
| + | Statikus esetben a Hartree-Fock egyenlet a következő alakba írható: | ||
| + | |||
| + | :<math> \mathcal{H} \phi_i = E_i \phi_i </math> | ||
| + | :<math> \mathcal{H} = -\frac{\hbar^2}{2m} \Delta_\vec{r} + V(\vec{r}) + U(\vec{r}) + K</math> | ||
| + | :<math> U(\vec{r}) = \int d^3 r' v(\vec{r}-\vec{r}') f(\vec{r}')</math> | ||
| + | |||
| + | és <math>K</math> hatása: | ||
| + | |||
| + | :<math> K \phi(\vec{r}) = \int d^3 r' \rho(\vec{r}, \vec{r}') v(\vec{r}-\vec{r}') \phi(\vec{r}')</math> | ||
| + | |||
| + | ahol az egyrészecske-sűrűségmátrix: | ||
| + | :<math> \rho(\vec{r}, \vec{r}') = \sum_i^N \phi^*_i(\vec{r}) \phi_i(\vec{r}') </math> | ||
| + | |||
| + | és az egyrészecske-eloszlásfüggvény: | ||
| + | :<math> f(\vec{r}) = \rho(\vec{r}, \vec{r}) </math> | ||
| + | |||
| + | === Időfüggő Hartree-Fock === | ||
| + | Ha dinamikát akarunk leírni, akkor a sűrűségmátrix időfejlődését kell tekintenünk. Ezt a Neumann-egyenlet írja le: | ||
| + | |||
| + | :<math> i \hbar \frac{\partial \rho}{\partial t} = [\mathcal{H},\rho]</math> | ||
| + | |||
| + | A problémát itt a párkölcsönhatás okozza, mert ez csatolódik a kétrészecske-sűrűségmátrixhoz. Ez elvileg az egyenletek végtelen hierarchiájához vezetne (az adott rendű sűrűségmátrix időfejlődése mindig csatolódik az eggyel magasabb rendű sűrűségmátrixhoz). Ezt egy közelítéssel oldjuk fel, nevezetesen a kétrészecske-sűrűségmátrixot az egyrészecskéssel fejezzük ki, ezáltal levágva a hierarchiát: | ||
| + | |||
| + | :<math> \rho^{(2)}(\vec{r}_1, \vec{r}_2, \vec{r}_3, \vec{r}_4) = \rho(\vec{r}_2, \vec{r}_3) \rho(\vec{r}_1, \vec{r}_4) - \rho(\vec{r}_2, \vec{r}_4) \rho(\vec{r}_1, \vec{r}_3)</math> | ||
| + | |||
| + | Így zárt egyenletrendszer kapható, amiben csak <math>\rho(\vec{r}, \vec{r}')</math> szerepel, de csak egyrészecske hatásokat vettünk figyelembe. | ||
| + | |||
| + | === Uehling-Uhlenbeck ütközési tag === | ||
| + | Ha a kétrészecske hatásokat is figyelembe szeretnénk venni, akkor azt perturbatíven lehet megtenni. Ha feltesszük, hogy az egyrészecske-sűrűségmátrix diagonális, akkor az egyrészecske-sűrűségelemek (<math>n_i</math>) mozgásegyenlete: | ||
| + | :<math> \frac{d n_i}{d t} = \frac{2\pi}{\hbar}\sum_{j} V^2_{ij} \delta(E_j-E_i)[n_j(1-n_i) - n_i(1-n_j)]</math> | ||
| + | Az analóg kifejezés a kétrészecskés esetre: | ||
| + | :<math> \frac{d n_i}{d t} = \frac{2\pi}{\hbar}\sum_{jlk} V^2_{ijkl} \delta(E_l+E_k-E_i-E_j)[n_l n_k (1-n_i)(1-n_j) - n_i n_j (1-n_l)(1-n_k)]</math> | ||
| − | + | <math>V_{ijkl}</math> a párkölcsönhatás mindkét esetben. Az időfüggő Hartree-Fock megközelítés tehát tovább javítható, ha a kétrészecske ütközéseket is be tudjuk építeni a modellbe. A fenti kétrészecskés tag adta a motivációt Uehlingnek és Uhlenbecknek, hogy egy klasszikus kinetikus egyenletet írjanak fel, ami a kétrészecskés ütközéseket is figyelembeveszi. Lényegében a Vlasov-egyenlethez hozzáadták a fenti kétrészecskés ütközési tagot a megfelelő klasszikus közelítések felhasználásával: | |
| − | + | ||
| − | + | :<math> | |
| − | + | \frac{\partial f}{\partial t} | |
| − | = | + | + \frac{\vec{p}}{m} \nabla_\vec{r} f |
| + | + \vec{F} \nabla_\vec{p} f | ||
| + | = -\int \frac{d \vec{p}_2 d \vec{p}_1' d \vec{p}_2'}{(2\pi)^6} \sigma v_{12} \times [f f_2 (1-f_1')(1-f_2') - f_1' f_2' (1-f)(1-f_2)]\delta^3(p + p_2 - p_1' - p_2') | ||
| + | </math> | ||
| + | |||
| + | itt <math>\sigma</math> az ütközési hatáskeresztmetszet, <math>v_{12}</math> pedig a potenciál mátrixeleme. | ||
== Gravitációsan kölcsönható soktestrendszerek == | == Gravitációsan kölcsönható soktestrendszerek == | ||
| − | + | A gravitációs soktest modellek nagyban hasonlítanak a fentebb ismertetettekre, csak a Maxwwell-egyenletek helyett például a gravitációs potenciál egyenletét kell csatolni a kinetikus egyenlethez. Itt még egy trükköt szoktak bevetni, nevezetesen a folytonos eloszlásfüggvényből Monte-Carlo módszerrel mintavételeznek pontrészecskéket, és rájuk számolják ki a párkölcsönhatásokat (esetleg megfelelően nagy távolságon elhanyagolva, vagy rácson blokkosítva). Ez egyszerűbb, mintha a folytonos anyageloszlásra kellene kiszámolni az erőhatást. | |
| − | |||
{{MSc záróvizsga}} | {{MSc záróvizsga}} | ||
A lap jelenlegi, 2011. június 16., 20:08-kori változata
Az alábbiakban összefoglaljuk a sok részecskét tartalmazó statisztikus rendszerek leírására szolgáló egyenleteket, továbbá néhány fontos alkalmazást is megemlítünk. Ezekből az egyenleteből származtatható további eredmények pedig a Transzportfolyamatok tételben kerülnek kifejtésre.
A sokrészecskés rendszerek leírásának három szintje van. A legalapvetőbb, mikroszkópikus szinten minden részecskét külön kezelünk. Ez a klasszikus esetben minden részecskére egy Newton-egyenlet csatolását jelenti. Egy Avogadro-szám nagyságrendű rendszerre ennek a megoldása lehetetlen. Ilyen esetekben célszerű a kinetikus megközelítésben számolni, ahol az egyrészecske tulajdonságokat statisztikus átalagokkal váltjuk fel, és ezekre az átlagokra írjuk fel az egyenleteket. Itt a változóink még mindig mikroszkópikus mennyiségek, de már jóval kevesebb van belőlük, mint a részecskék száma. A harmadik szint a makroszkópikus tárgyalás, ahol már a makroszkópikus állapotjelzőkre vonatkoznak az egyenletek, mint például hőmérséklet, nyomás stb. Az alábbiakban a kinetikus tárgyalásmóddal foglalkozunk.
Tartalomjegyzék
Klasszikus sokrészecskerendszerek leírása
Amikor nagyon sok részecskének a jellemzőit kell leírni, akkor célszerű mindent eloszlásfüggvényekkel kifejezni. Az eloszlásfüggvény felintegrálva részecskeszámot ad. Meg kell azonban különböztetni, hogy hány részecskére vonatkozik az eloszlásfüggvény. Speciálisan az egyrészecske-eloszlásfüggvény azt mondja meg, hogy mekkra valószínűséggel találunk a 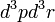 fázistérfogatban 1 részecskét (vagy N-et, a normálás konvenció kérdése), az egyszerűség kedvéért 3 dimenzióra specializálva a tárgyalást:
fázistérfogatban 1 részecskét (vagy N-et, a normálás konvenció kérdése), az egyszerűség kedvéért 3 dimenzióra specializálva a tárgyalást:
Ezzel szemben az általános N részecske-eloszlásfüggvény azt mondja meg, hogy mekkora valószínőséggel találjuk egy időben az első részecskét az 1. fázistér-pontban, a második részecskét a 2. fázistér pontban, ... stb.:
A Liouville-egyenlet
Az eloszlásfüggvények megváltozásának leírásához valamilyen mozgásegyenletre van szükségünk. A legegyszerűbb és egyben legáltalánosabb ilyen egyenlet a Liouville-egyenlet, amely az N részecske-eloszlásfüggvényre vonatkozik:
Itt 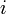 indexeli az
indexeli az 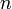 darab részecskét,
darab részecskét, 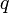 a kanonikus koordináta,
a kanonikus koordináta, 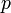 a konjugált impulzus és az időderiváltakat a szokásos módon a Hamilton operátor adja:
a konjugált impulzus és az időderiváltakat a szokásos módon a Hamilton operátor adja:
Fontos kiemelni, hogy a Liouville-egyenlet egy 6n dimenziós egyenlet (szemben a későbbiekkel). Tömören megfogalmazva a fázistérfogat megmaradását fejezi ki a mozgás trajektóriája mentén. Speciálisan 1 klasszikus részecskére az egyenlet:
Molekula dinamika
Nagyon nagy vonalakban csak arról van szó, hogy a Liouville-egyenletet tekintjük úgy, hogy a deriváltakat a Newton-féle erőtörvény adja.
A Boltzmann-egyenlet
A Boltzmann-egyenlet Boltzmann-egyenlet az előzőekkel szemben az egyrészecske-eloszlásfüggvényre vonatkozó mozgásegyenletet adja meg. Alapvetően ez is a fázistérfogat megmaradására épít, amely külső erőhatás esetén ütközések nélkül:
A baloldal az eloszlásfüggvény teljes deriváltja ha 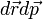 infinitezimális. Ha ütközések is vannak, azok a jobboldalra írhatóak. Ezekkel együtt a Boltzmann-egyenlet:
infinitezimális. Ha ütközések is vannak, azok a jobboldalra írhatóak. Ezekkel együtt a Boltzmann-egyenlet:
Azaz az ütközési tagtól eltekintve visszakaptuk a Liouville-egyenlet fenti speciális esetét. Boltzmann nagy eredménye az volt, hogy az ütközési tagra is tudott jól használható feltevést tenni az egyrészecske-eloszlásfüggvényekkel kifejezve. Ez a molekuláris káosz feltevés, amely arra épül, hogy a részecskék sebességei korrelálatlanok az ütközés előtt és után, továbbá függetlenek a helytől. Ennek a segítségével az ütközési tag:
ahol az 1, 2 indexek az egyik és másik részecske adatait indexelik, a vesszőtlen menyiségek az ütközés előtti, a vesszősek az ütközés utániakat jelölik, 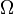 a relatív sebességek megváltozási szöge,
a relatív sebességek megváltozási szöge, 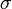 az ütközési hatáskeresztmetszet.
az ütközési hatáskeresztmetszet.
Relaxációs közelítés az ütközési tagra
Az egyik leggyakrabban használt és legegyszerűbb közelítés a Boltzmnn-egyenlet ütközési tagjára, az úgynevzett relaxációs idő közelítés. Ez akkor igaz, ha igen közel vagyunk az egyensúlyi eloszláshoz, 1 valószínűséggel találhatunk betöltetlen állapotokat (az 1-f jellegű tagokat 1-el közelíthetjük), továbbá az ütközés előtti és utáni állapotokra teljesül a részletes egyensúly elve. Ekkor:
ahol 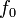 az egyensúlyi eloszlás Fermi-Dirac statisztika esetén:
az egyensúlyi eloszlás Fermi-Dirac statisztika esetén:
Ha eltekintünk a sűrűség gradiensektől és a külső erőhatásoktól, akkor egyszerűen megoldható a Boltzmann-egyenlet:
A Vlasov-egyenlet
Vlasov szerint a Boltzmann-féle kinetikus leírás nem jó hosszútávú kölcsönhatásokkal csatolt sokrészecskerendszerek leírására (ő az elektromos plazma leírására használta, de nyilván a gravitáció is hasonló problémákat vet fel). Egyrészt eleoktronszórásos kísérletekkel való ellentmondás, másrészt a plazmaoszcillációkkal való ellentmondás, harmadrészt a kinetikus tagok divergenciái miatt fellépő problémák miatt egy másik kinetikus leírást keresett, amely a Boltzmann-egyenletek és a Maxwell-egyenletek csatolásával leírná az elektronok és a pozitív töltés atomtörzsek egymásrahatását.
Bár az irodalom erősen keveri az elnevezéseket, de úgy fest, hogy a Vlasov-egyenlet nem más, mint a Boltzmann-egyenlet ütközési tag nélkül, és az erőhatás az elektromágneses hatásokból származik, csatolva a Maxwell-egyenletekkel:
Itt "+" a pozitív töltésű, "-" a negatív töltésű részecskék paramétereit indexeli. Fontos látni, hogy az elektromágneses tér forrásául nem az egyes részecskék, hanem a kiátlagolt eloszlásfüggvények szolgálnak.
Kvantumos sokrészecskerendszerek leírása
Legegyszerűbb (nem-relativisztikus) esetben az időfüggő Schrödinger-egyenletet kellene megoldani:
ahol 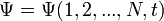 az N-részecske hullámfüggvény,
az N-részecske hullámfüggvény, 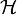 pedig a sokrészecske Hamilton-operátor. Ennek precíz megoldása szintén esélytelen.
pedig a sokrészecske Hamilton-operátor. Ennek precíz megoldása szintén esélytelen.
A Hartree-Fock módszer
Statikus esetben egy jó közelítés a Hartree-Fock módszer. Közelítsük a sokrészecske-hullámfüggvényt egyrészecske-hullámfüggvények kombinációjaként, számoljuk ki a kölcsönhatások átlagait ezekkel, majd oldjuk meg ezekre egyenként az egyrészecske-egyenleteket. Az így kapott új hullámfüggvényekkel újrakezdhető az iteráció, és egy önkonzisztens módszert kaphatunk.
A Hartree és a Hartree-Fock módszer abban különbözik, hogy milyen módon bontják fel a sokrészecske-hullámfüggvényt. Előbbi simán szorzatalakban, utóbbi Slater-determináns alakban teszi ezt, ez nyilván jobb felírás (fermionokra), mert figyelembe veszi a hullámfüggvény antiszimmetrikusságát.
Statikus esetben a Hartree-Fock egyenlet a következő alakba írható:
és 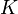 hatása:
hatása:
ahol az egyrészecske-sűrűségmátrix:
és az egyrészecske-eloszlásfüggvény:
Időfüggő Hartree-Fock
Ha dinamikát akarunk leírni, akkor a sűrűségmátrix időfejlődését kell tekintenünk. Ezt a Neumann-egyenlet írja le:
A problémát itt a párkölcsönhatás okozza, mert ez csatolódik a kétrészecske-sűrűségmátrixhoz. Ez elvileg az egyenletek végtelen hierarchiájához vezetne (az adott rendű sűrűségmátrix időfejlődése mindig csatolódik az eggyel magasabb rendű sűrűségmátrixhoz). Ezt egy közelítéssel oldjuk fel, nevezetesen a kétrészecske-sűrűségmátrixot az egyrészecskéssel fejezzük ki, ezáltal levágva a hierarchiát:
Így zárt egyenletrendszer kapható, amiben csak 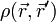 szerepel, de csak egyrészecske hatásokat vettünk figyelembe.
szerepel, de csak egyrészecske hatásokat vettünk figyelembe.
Uehling-Uhlenbeck ütközési tag
Ha a kétrészecske hatásokat is figyelembe szeretnénk venni, akkor azt perturbatíven lehet megtenni. Ha feltesszük, hogy az egyrészecske-sűrűségmátrix diagonális, akkor az egyrészecske-sűrűségelemek (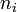 ) mozgásegyenlete:
) mozgásegyenlete:
Az analóg kifejezés a kétrészecskés esetre:
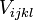 a párkölcsönhatás mindkét esetben. Az időfüggő Hartree-Fock megközelítés tehát tovább javítható, ha a kétrészecske ütközéseket is be tudjuk építeni a modellbe. A fenti kétrészecskés tag adta a motivációt Uehlingnek és Uhlenbecknek, hogy egy klasszikus kinetikus egyenletet írjanak fel, ami a kétrészecskés ütközéseket is figyelembeveszi. Lényegében a Vlasov-egyenlethez hozzáadták a fenti kétrészecskés ütközési tagot a megfelelő klasszikus közelítések felhasználásával:
a párkölcsönhatás mindkét esetben. Az időfüggő Hartree-Fock megközelítés tehát tovább javítható, ha a kétrészecske ütközéseket is be tudjuk építeni a modellbe. A fenti kétrészecskés tag adta a motivációt Uehlingnek és Uhlenbecknek, hogy egy klasszikus kinetikus egyenletet írjanak fel, ami a kétrészecskés ütközéseket is figyelembeveszi. Lényegében a Vlasov-egyenlethez hozzáadták a fenti kétrészecskés ütközési tagot a megfelelő klasszikus közelítések felhasználásával:
itt 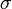 az ütközési hatáskeresztmetszet,
az ütközési hatáskeresztmetszet, 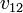 pedig a potenciál mátrixeleme.
pedig a potenciál mátrixeleme.
Gravitációsan kölcsönható soktestrendszerek
A gravitációs soktest modellek nagyban hasonlítanak a fentebb ismertetettekre, csak a Maxwwell-egyenletek helyett például a gravitációs potenciál egyenletét kell csatolni a kinetikus egyenlethez. Itt még egy trükköt szoktak bevetni, nevezetesen a folytonos eloszlásfüggvényből Monte-Carlo módszerrel mintavételeznek pontrészecskéket, és rájuk számolják ki a párkölcsönhatásokat (esetleg megfelelően nagy távolságon elhanyagolva, vagy rácson blokkosítva). Ez egyszerűbb, mintha a folytonos anyageloszlásra kellene kiszámolni az erőhatást.
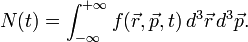
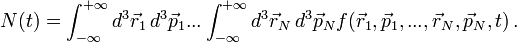
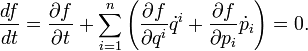
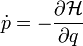
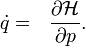
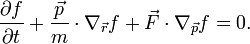
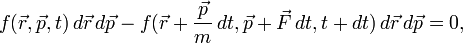
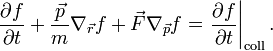
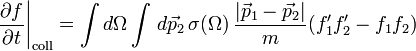
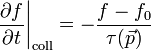
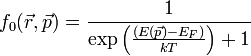
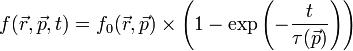
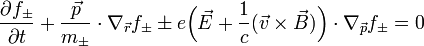
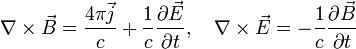
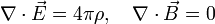
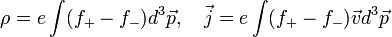
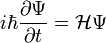
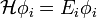
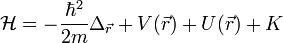
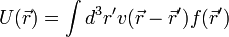
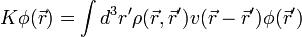
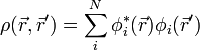
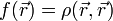
![i \hbar \frac{\partial \rho}{\partial t} = [\mathcal{H},\rho]](/images/math/a/d/8/ad8eb48a7ab263e635a6a1540c17454e.png)
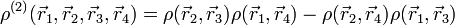
![\frac{d n_i}{d t} = \frac{2\pi}{\hbar}\sum_{j} V^2_{ij} \delta(E_j-E_i)[n_j(1-n_i) - n_i(1-n_j)]](/images/math/0/c/9/0c9f474a77f5a8b942c21770b8fca1c1.png)
![\frac{d n_i}{d t} = \frac{2\pi}{\hbar}\sum_{jlk} V^2_{ijkl} \delta(E_l+E_k-E_i-E_j)[n_l n_k (1-n_i)(1-n_j) - n_i n_j (1-n_l)(1-n_k)]](/images/math/4/c/6/4c6777d90d043ffe0703c48b48e88a00.png)
![\frac{\partial f}{\partial t}
+ \frac{\vec{p}}{m} \nabla_\vec{r} f
+ \vec{F} \nabla_\vec{p} f
= -\int \frac{d \vec{p}_2 d \vec{p}_1' d \vec{p}_2'}{(2\pi)^6} \sigma v_{12} \times [f f_2 (1-f_1')(1-f_2') - f_1' f_2' (1-f)(1-f_2)]\delta^3(p + p_2 - p_1' - p_2')](/images/math/9/a/a/9aa2b895501ef5df51d303bbbc2e838d.png)