„Véletlen gráfok generálása, tulajdonságai '12” változatai közötti eltérés
(Új oldal, tartalma: „Rengeteg mindent fel lehet írni gráf alakban: internetes honlapok, szociális hálók, metabolikus folyamatok, szerzőségi hálók, tápláléklánc, körfolyamatok a f…”) |
|||
| (3 közbenső módosítás, amit egy másik szerkesztő végzett, nincs mutatva) | |||
| 11. sor: | 11. sor: | ||
*Csúcs fokszáma: a csúcs kapcsolatainak száma (irányított gráfnál lehet beszélni bejövő és kimenő fokszámról). | *Csúcs fokszáma: a csúcs kapcsolatainak száma (irányított gráfnál lehet beszélni bejövő és kimenő fokszámról). | ||
**Fokszám-eloszlás: egy gráf teljes fokszám-gyakoriság diagramja. <math>p<k> = N_k / N</math> (ahol <math>N_k</math> a k fokszámú csúcsok száma, N pedig a csúcsok száma | **Fokszám-eloszlás: egy gráf teljes fokszám-gyakoriság diagramja. <math>p<k> = N_k / N</math> (ahol <math>N_k</math> a k fokszámú csúcsok száma, N pedig a csúcsok száma | ||
| − | * Csúcs klaszterezettségi együtthatója: (csoporterősségi együttható) | + | * Csúcs klaszterezettségi együtthatója: (csoporterősségi együttható, a szomszédok közti lehetséges élek hányad része létezik) |
<math>c_i = \frac{2e_i}{k_i(k_i-1)}</math>, ahol <math>e_i</math> az i-edik csúcs szomszédai közti élek száma. Átlagos klaszterezettség: <math><c> = \frac{1}{N}\sum(c_i)</math> | <math>c_i = \frac{2e_i}{k_i(k_i-1)}</math>, ahol <math>e_i</math> az i-edik csúcs szomszédai közti élek száma. Átlagos klaszterezettség: <math><c> = \frac{1}{N}\sum(c_i)</math> | ||
| 36. sor: | 36. sor: | ||
*Csúcsok növelésével exponenciálisan nő a kapcsolatszám | *Csúcsok növelésével exponenciálisan nő a kapcsolatszám | ||
| − | *A fokszámeloszlás | + | *A fokszámeloszlás Binomiális-eloszlás lesz (analitikusan is levezethető) |
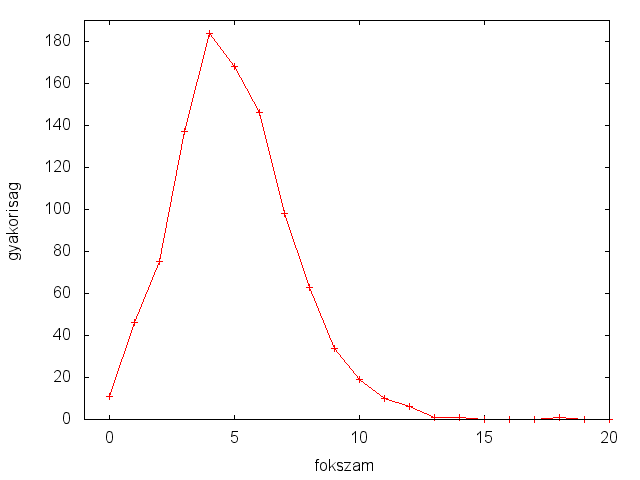
[[Kép:RandomGraph_DD.png|center|250px|thumb|N=1000 random gráf fokszámeloszlása (p kicsi)]] | [[Kép:RandomGraph_DD.png|center|250px|thumb|N=1000 random gráf fokszámeloszlása (p kicsi)]] | ||
*Kisvilág tulajdonság, ha összefüggő. Szinte mindig összefüggő, mivel az óriáskomponens (a csúcsok legnagyobb részét tartalmazó algráf, más szóval klaszter) gyorsan kialakul, <math>p \sim \frac{1}{N} + \epsilon</math>, ahol p az összekötési valószínűség, N a csúcsok száma és <math>\epsilon</math> egy kicsi szám. Az egyes komponenseken belül is kisvilág tulajdonság | *Kisvilág tulajdonság, ha összefüggő. Szinte mindig összefüggő, mivel az óriáskomponens (a csúcsok legnagyobb részét tartalmazó algráf, más szóval klaszter) gyorsan kialakul, <math>p \sim \frac{1}{N} + \epsilon</math>, ahol p az összekötési valószínűség, N a csúcsok száma és <math>\epsilon</math> egy kicsi szám. Az egyes komponenseken belül is kisvilág tulajdonság | ||
| 43. sor: | 43. sor: | ||
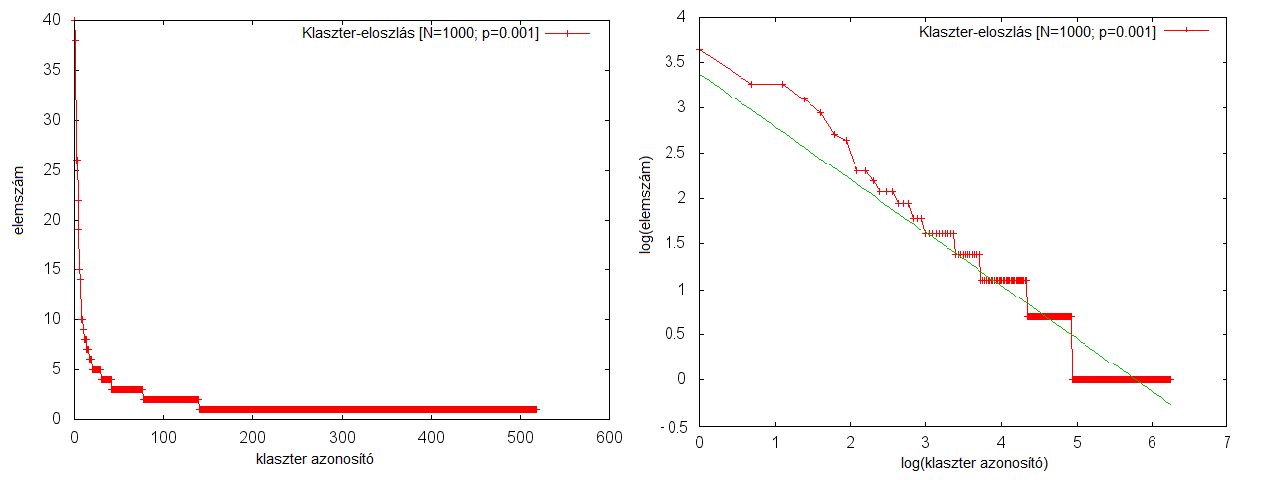
A klaszterek méreteloszlása hatványfüggvény szerint csökken: | A klaszterek méreteloszlása hatványfüggvény szerint csökken: | ||
[[Kép:Cluster_distr.png|center|500px|thumb|]] | [[Kép:Cluster_distr.png|center|500px|thumb|]] | ||
| + | |||
| + | ==Konfigurációs modell== | ||
| + | |||
| + | *Feladat: adott fokszám-eloszlású véletlen gráf generálása. | ||
| + | *"Recept": húzzunk N-szer p(k)-ból (csúcsokat fél élekkel), majd kössük őket össze egymással. | ||
| + | ::könnyen előfordulhatnak hurkok, ezért a nagy fokszámú csúcstól induljunk. | ||
| + | :Ez még nem tekinthető véletlennek, randomizálás szükséges: ennek egyik lehetséges módja az élek átkötése a fokszámok megőrzésével (Link Randomization). | ||
==Watts-Strogratz gráf== | ==Watts-Strogratz gráf== | ||
| 70. sor: | 77. sor: | ||
Ravasz és Barabási hierarchikus modelljének lépései: | Ravasz és Barabási hierarchikus modelljének lépései: | ||
* Öt csúcs - teljesen összekötve | * Öt csúcs - teljesen összekötve | ||
| − | * 4 másolat a teljes gráfról, melynek magjai összekötöttek, | + | * 4 másolat a teljes gráfról, melynek magjai összekötöttek, szélső csúcsai pedig az eredeti maggal összekötöttek |
* első lépéstől ismétlés... | * első lépéstől ismétlés... | ||
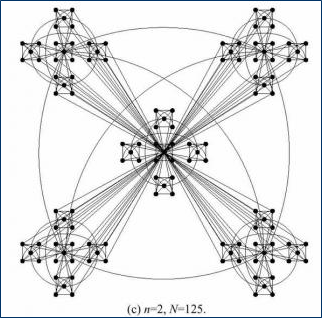
[[Kép:Ravasz_Barabasi.png|center|200px|thumb|]] | [[Kép:Ravasz_Barabasi.png|center|200px|thumb|]] | ||
A lap jelenlegi, 2012. június 17., 14:05-kori változata
Rengeteg mindent fel lehet írni gráf alakban: internetes honlapok, szociális hálók, metabolikus folyamatok, szerzőségi hálók, tápláléklánc, körfolyamatok a fizikában és a biológiában, linux kernel stb.
Tartalomjegyzék
Alapfogalmak
- Egy gráf csúcsokból és élekből áll. A gráf lehet:
- Egyszerű gráf (két pont között csak 1 él, nincs hurok egy csúcsra); Multi gráf (két pont között lehet több él, nincs hurok egy csúcsra); Pszeudo gráf (két pont között lehet több él és lehet egy csúcson hurok)
- Irányított/Irányítatlan
- Súlyozott/Súlyozatlan
- Címkézett gráf: csúcs- és/vagy él-címkézett (élek/csúcsok egyéni azonosítóval rendelkeznek)
- Biparit gráf: két fajta csúcs van és élek csak a különböző fajtájú csúcsok közt vannak (pl.: filmszínészek hálózata)
- Gráf reprezentációja: mutatókkal, él-listákkal, vagy összekötöttségi mátrixokkal.
- Csúcs fokszáma: a csúcs kapcsolatainak száma (irányított gráfnál lehet beszélni bejövő és kimenő fokszámról).
- Fokszám-eloszlás: egy gráf teljes fokszám-gyakoriság diagramja.
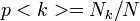 (ahol
(ahol 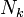 a k fokszámú csúcsok száma, N pedig a csúcsok száma
a k fokszámú csúcsok száma, N pedig a csúcsok száma
- Fokszám-eloszlás: egy gráf teljes fokszám-gyakoriság diagramja.
- Csúcs klaszterezettségi együtthatója: (csoporterősségi együttható, a szomszédok közti lehetséges élek hányad része létezik)
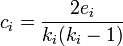 , ahol
, ahol  az i-edik csúcs szomszédai közti élek száma. Átlagos klaszterezettség:
az i-edik csúcs szomszédai közti élek száma. Átlagos klaszterezettség: 
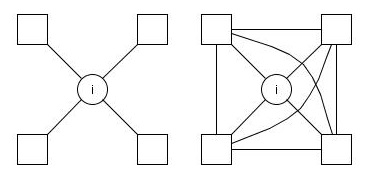
Szemléletes jelentés: Ha 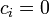 , akkor "csillag" - ha
, akkor "csillag" - ha 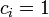 , akkor "klikk"
, akkor "klikk"
- Alternatív Klaszterezettség definíció I:
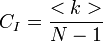 , ahol <k> az átlagos fokszám, N pedig az összes csúcs száma
, ahol <k> az átlagos fokszám, N pedig az összes csúcs száma - Alternatív Klaszterezettség definíció II:
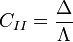 , ahol
, ahol 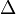 a redszerben előforduló 3 teljesen összekötött csúcs számossága,
a redszerben előforduló 3 teljesen összekötött csúcs számossága, 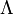 pedig 3 pont 2 éllel összekötött részek számossága (ahogy a szimbólumok alakja is utal ezekre)
pedig 3 pont 2 éllel összekötött részek számossága (ahogy a szimbólumok alakja is utal ezekre) - Távolság: (
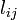 ) az a minimális lépésszám i és j csúcsok között, ami alatt el lehet jutni i-ből j-be az éleket követve. (irányítatlan gráfon
) az a minimális lépésszám i és j csúcsok között, ami alatt el lehet jutni i-ből j-be az éleket követve. (irányítatlan gráfon 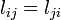 , irányított gráfon ez nem feltétlen teljesül.)
, irányított gráfon ez nem feltétlen teljesül.)
Kisvilág tulajdonság
Legyen a gráf összes csúcsának száma N. Két tetszőleges csúcs közötti legrövidebb út: legkevesebb csúcs érintésével. Legrövidebb utak átlagos hossza: l.
Kisvilág tulajdonság: 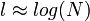
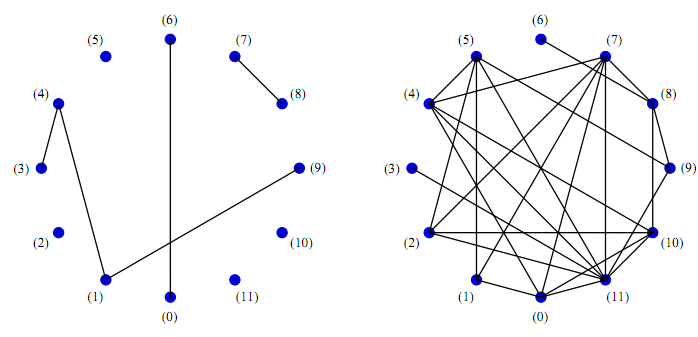
Erdős-Rényi gráf
- N csúcsból áll
- Minden két csúcs között p valószínűséggel él
Tulajdonságok
- Csúcsok növelésével exponenciálisan nő a kapcsolatszám
- A fokszámeloszlás Binomiális-eloszlás lesz (analitikusan is levezethető)
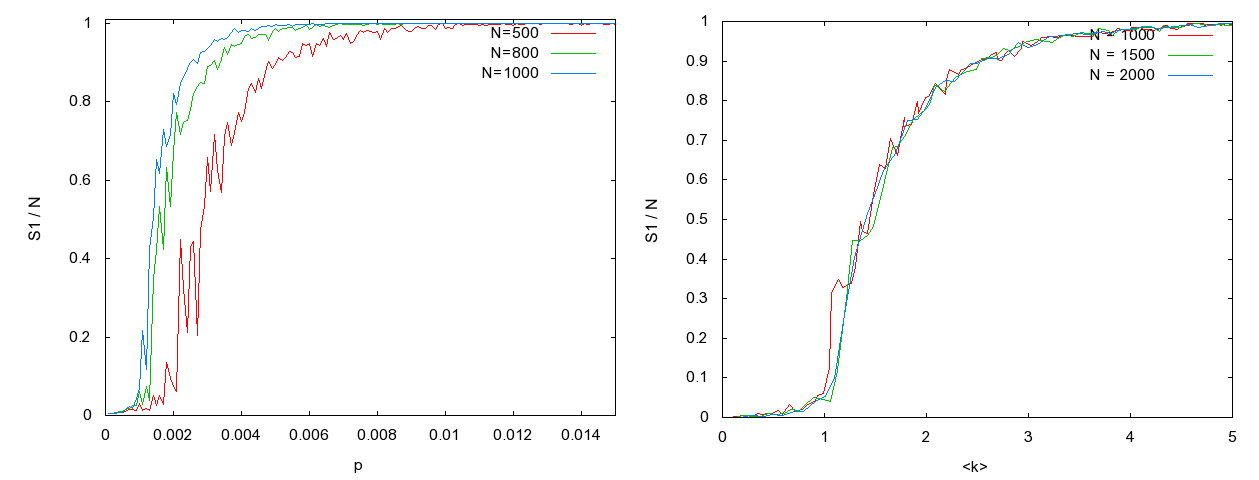
- Kisvilág tulajdonság, ha összefüggő. Szinte mindig összefüggő, mivel az óriáskomponens (a csúcsok legnagyobb részét tartalmazó algráf, más szóval klaszter) gyorsan kialakul,
 , ahol p az összekötési valószínűség, N a csúcsok száma és
, ahol p az összekötési valószínűség, N a csúcsok száma és  egy kicsi szám. Az egyes komponenseken belül is kisvilág tulajdonság
egy kicsi szám. Az egyes komponenseken belül is kisvilág tulajdonság
A klaszterek méreteloszlása hatványfüggvény szerint csökken:
Konfigurációs modell
- Feladat: adott fokszám-eloszlású véletlen gráf generálása.
- "Recept": húzzunk N-szer p(k)-ból (csúcsokat fél élekkel), majd kössük őket össze egymással.
- könnyen előfordulhatnak hurkok, ezért a nagy fokszámú csúcstól induljunk.
- Ez még nem tekinthető véletlennek, randomizálás szükséges: ennek egyik lehetséges módja az élek átkötése a fokszámok megőrzésével (Link Randomization).
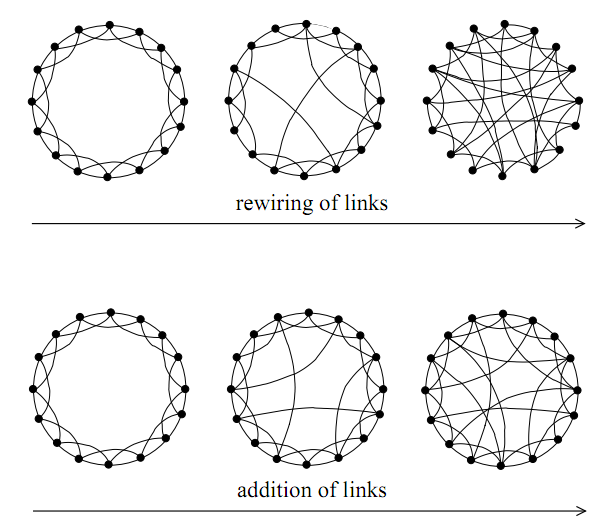
Watts-Strogratz gráf
A "kisvilág" modell, tetszőleges D dimenzióban megvalósítható.
- N csúcs, kiinduláskor rendezett rács, szabályos k-szomszédság
- Két módszer: "átdrótozás" (rewiring), vagy "levágások" (shortcuts). Előbbinél a meglévő éleket helyezzük át, utóbbinál új éleket vezetünk be két csúcs között - mindkét esetben p valószínűséggel tesszük ezt minden csúcspárra
- Az átlagos legrövidebb út hamarabb csökken, mint a klaszterezettség, egyszerre kisvilág és klaszterezett
Barabási-Albert gráf
Preferenciális csatolás (preferential attachment) modell.
- M db kezdőcsúcs tetszőlegesen összekötve
- Minden lépésben egy új csúcs, E db éllel
- Véletlenszerű, hogy melyik csúcshoz csatlakoznak az új élek, de a meglévő csúcsok fokszáma alapján preferencia:
 , ahol
, ahol 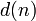 az n-edik csúcs fokszáma
az n-edik csúcs fokszáma
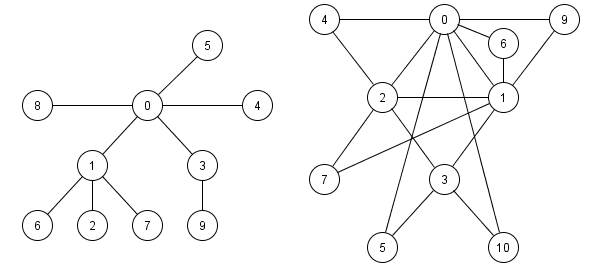
Ha E = 1, akkor 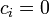 - fa gráfot fogunk kapni:
- fa gráfot fogunk kapni:
Tulajdonságai
- A fokszámeloszlás hatványfüggvényt követ
- Kisvilág
- NEM klaszterezett
Egy modell a három tulajdonsággal
Ravasz és Barabási hierarchikus modelljének lépései:
- Öt csúcs - teljesen összekötve
- 4 másolat a teljes gráfról, melynek magjai összekötöttek, szélső csúcsai pedig az eredeti maggal összekötöttek
- első lépéstől ismétlés...
Ez a modell: kisvilág, klaszterezett és skálafüggetlen, DE! determinisztikus (nem véletlen).
Robosztusság
Más néven ellenállóság véletlen hibákkal, vagy támadásokkal szemben.
Miért fontos? Robosztus számítógép-hálózatok, fajok védelme, járvány-védelem, információ-terjedés elleni "védelem" stb.
Fontos az adott csúcs/él centralitása ("központi szerepének" jellemzése) - ezeket lehet érdemes "támadni"
- Fok-centralitás:
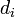 - a csúcs fokszáma. ("Népszerűség")
- a csúcs fokszáma. ("Népszerűség") - Közelség-centralitás:
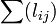 - a többi csúcshoz vezető min. utak összege
- a többi csúcshoz vezető min. utak összege - Köztesség-centralitás:
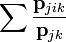 - az áthaladó utak száma
- az áthaladó utak száma
Erdős-Rényi gráf:
- Gyakorlatilag mindegy, hogy irányított vagy véletlen támadást hajtunk végre, mert nincsenek kitüntetett csúcsok
Barabási-Albert gráf:
- A véletlen támadással szemben ellenállóbb (kicsi a valószínűsége, hogy fontos csúcs hibásodik meg), viszont az irányított támadásra sokkal érzékenyebb.
- A WS gráf véletlen támadással és célzottal szemben is ellenálló, bár célzott támadás esetén hamar elveszti a kisvilág tulajdonságát. (És ilyet építeni a k-szomszédság miatt a gyakorlatban nem érdemes.)
Források: Claudius Gros - Complex and Adaptive Dynamcial Systems; Gulyás László - Társadalmi hálózatok és modelljeik előadás diák