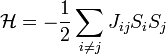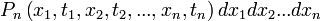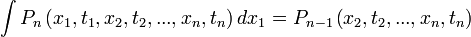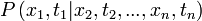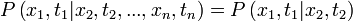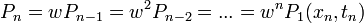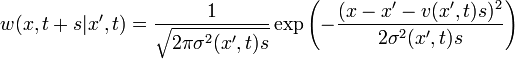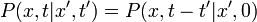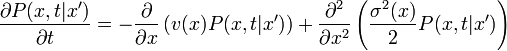„Sztochasztikus folyamatok” változatai közötti eltérés
(→Kauffman-hálózat) |
a (→Spinüvegek) |
||
| (2 közbenső módosítás, amit 2 másik szerkesztő végzett, nincs mutatva) | |||
| 28. sor: | 28. sor: | ||
de <math>J</math> egy véletlen valószínűségi változó Gauss-eloszlással. Ebben az esetben az átlagos szabadenergia kiszámolható a rendszerre zárt alakban, két fizikailag értelems paraméterrel kifejezve: az egyik paraméter eredő mágnesezettség jellegű, a másik a mágnesezettség szórását jellemzi. A spinüveg helyzetnek az felel meg, amikor az eredő mágnesezettség eltűnik, de a szórás véges, szemben például a ferromágneses renddel, ahol az eredő mágnesezettség nem zérus. | de <math>J</math> egy véletlen valószínűségi változó Gauss-eloszlással. Ebben az esetben az átlagos szabadenergia kiszámolható a rendszerre zárt alakban, két fizikailag értelems paraméterrel kifejezve: az egyik paraméter eredő mágnesezettség jellegű, a másik a mágnesezettség szórását jellemzi. A spinüveg helyzetnek az felel meg, amikor az eredő mágnesezettség eltűnik, de a szórás véges, szemben például a ferromágneses renddel, ahol az eredő mágnesezettség nem zérus. | ||
| − | A fázisteret két paraméterrel lehet felmérni: a csatolás relatív szórásával (a fenti Gauss | + | A fázisteret két paraméterrel lehet felmérni: a csatolás relatív szórásával (a fenti Gauss szórása osztva az átlaggal) valamint a csatolás szórásának és a hőmérsékleti energiának (kT) az arányával. Ezen a diagrammon a spinüveg fázis akkor jön létre, amikor a csatolás erősebb a hőmérsékleti fluktuációknál, de a relatív szórása nagy (Megyjegyzés: az ábra vízszintes tengelyén a relatív szórás reciproka van: az átlag osztva a szórással). |
| + | |||
| + | [[Fájl:SpinGlass.PNG]] | ||
== Markov-lánc, Markov-folyamatok == | == Markov-lánc, Markov-folyamatok == | ||
| 63. sor: | 65. sor: | ||
:<math>\frac{\partial P(x, t|x')}{\partial t} = -\frac{\partial}{\partial x}\left( v(x)P(x, t|x') \right) + \frac{\partial^2}{\partial x^2}\left( \frac{\sigma^2(x)}{2}P(x, t|x') \right)\,</math> | :<math>\frac{\partial P(x, t|x')}{\partial t} = -\frac{\partial}{\partial x}\left( v(x)P(x, t|x') \right) + \frac{\partial^2}{\partial x^2}\left( \frac{\sigma^2(x)}{2}P(x, t|x') \right)\,</math> | ||
| + | ===Brown-mozgás=== | ||
| + | Esetleg meg lehet említeni/felírni a [http://mafihe.hu/~wiki/wiki/index.php/V%C3%A9lFiz_1.t%C3%A9tel#1._t.C3.A9tel:_Brown-mozg.C3.A1s:_Einstein_levezet.C3.A9se Brown-mozgást], mint példát diszkrét Markov-folyamatra | ||
| + | |||
| + | Lásd még a [[Transzportfolyamatok]] tétel végét. | ||
{{MSc záróvizsga}} | {{MSc záróvizsga}} | ||
A lap jelenlegi, 2011. június 15., 12:35-kori változata
Az alábbiakban néhány véletlenszerű folyamatot és ezek leírási módszereit tárgyaljuk.
Kauffman-hálózat
Egyes a természetben előforduló folyamat-hálózatoknak a modellezésére egy igen végletekig egyszerűsített megközelítés is hasznos kiindulási pontot szolgáltathat. A Kauffman-hálózat nem más, mint egy gráf, melyben irányított élek vannak, és a csomópontokban csak két féle érték engedett meg (pl. 0 - 1 v. +1 - -1). A csomópontokban ezeken a bináris értékeken értelmezett függvények vannak, amelyek minden időlépésben a befutó élek által összekapcsolt csomópontok értékeiből (és esetleg az aktuálisból) előállítanak egy előre meghatározott szabály szerint egy új értéket, és azt beírják az aktuális csomópontba. A rendszert diszkrét időlépésekben fejlesztjük.
Kauffman először az élőlények genetikai tartalmának kifejeződését vizsgálta a sejtek különböző differenciáltságán: a különböző funkciójú sejtek a különböző gének működésének hatására alakulnak ki, Kauffman modelljében ezeknek a gráfdinamika határciklusai felelnek meg. Később az ilyne alapú modellek számos más bonyolult, az élőlényekkel kapcoslatos problémában sikerrel kerültek alkalmazásra, egyetlen másik példát hozva a neurális hálózatok egyszerűbb, könyebben kezelhető modelljei is ilyen alapúak.
Ez a modell számos érdekes folyamatot mutat: vannak kaotikus é reguláris mintázatok is benne. A rendszer azért sztochasztikus, mert a gráfban a kapcsolatokat és a csúcsokhoz rendelt időléptetési függvényeket véletlenszerűen osztjuk ki. Ilyen függvények tipikusan az egyszerű logikai függvényke lehetnek: OR, XOR, AND, vagy véletlenszerű, stb...
Ha 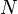 csomópont van a grásban, akkor a rendszer állapottere
csomópont van a grásban, akkor a rendszer állapottere 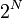 , ezért az időfejlődésben legfeljebb ennyi különböző helyzetben lehet a rendszer, igne gyakran azonban rövidebb ciklusok is előfordulnak, illetve léteznek fixpont atraktorok, amik több különböző kiindulási értékből/kiotszásból is ugyanabba a helyzetbe, vagy ciklusba vezetik a rendszert.
, ezért az időfejlődésben legfeljebb ennyi különböző helyzetben lehet a rendszer, igne gyakran azonban rövidebb ciklusok is előfordulnak, illetve léteznek fixpont atraktorok, amik több különböző kiindulási értékből/kiotszásból is ugyanabba a helyzetbe, vagy ciklusba vezetik a rendszert.
Egy ilyen egyszerűsített modellben nyilván nem a rendszer különböző állapotainak van lényegi jelentése, hanem a változásokra adott válaszainak, a robosztusságnak (hibatűrés, külső hatások kivédése), közeli állapotokból való szétfejlődés sebessége. Ha a rendszer állapotai között bevezetjük a Hamming-távolságot, ami a különböző állapotú elemek számát jelöli, akkor van egy mérőszámunk, amivel az információ vesztést, vagy akár egy skalárisszorzat jellegű mennyiséget is definiálhatunk. Ez utóbbinak a hosszú idejű határértéke rendparaméterként váalsztja el a kaotikus és a rendezett viselkedésű rendszer állapotokat. Ezt a kritikus pontot is hatvány függvények jellemzik számos válasz függvény viselkedésében, például az attraktorok számában, vagy az átlagos határciklus-hosszban.
Példaként, a határciklus-hossz egy fontos, a valóságban is meghatározható mennyiség lehet: ha ez túl nagy, akkor az élőlény életideje alatt nem alaulhatnak ki a megfelelő stabil dinamikai struktúrák (Kauffman esetében a különböző differenciáltságú sejtek): éppen ez a helyzet a kaotikus tartományban. A mésik végletként a túlságosan fix (befagyott) állapot sem jó, ugyanis nem tudja biztosítani az evolúcióshoz szükséges változóképességet. Ezért Kauffmann azt a javaslatot tette, hogy az élő rendszrek valójában a káosz szélén működnek, azaz profitálnka bizonyos mértékben a stabilitásból és a változékonyságból is.
Konkrétan az élesztő sejt osztódásának Kauffman-modellje teljesen jól adja vissza a gének és a fehérjék aktiválódási sorrendjét összevetve a kísérletekkel, hasonló összekötöttséget és kritikus közelé paramétereket reprodukálva.
Spinüvegek
Közismert, hogyha mágneses momentumokat (spineket) akarunk elhelyezni egy háromszögrácson, antiferromágneses csatolás mellett, akkor az frusztrált lesz: például egy háromszög két csúcsára leteszünk ellenkező beállással 1-1 spint, akkor a harmadiknak nincs optimális beállása.
A spinüvegekben hasonló frusztrációk vannak, rendezetlen rácson. Úgy lehet elképzelni, hogy a spinek véletlenszerű helyeken, véletlenszerű (ferro- vagy antiferromágneses) kölcsönhatásokkal vannak összekötve. Ennek eredményeképpen a külső térre adott válaszuk igen bonyolult, számos különböző időskálán zajlik. A leírásuk is igen nehézkes.
Egy konkrét gyakran használt modellben, a Sherrington-Kirkpatrick modellben a spinek között a szokásos Hamilton írja le a kölcsönhatást:
de 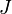 egy véletlen valószínűségi változó Gauss-eloszlással. Ebben az esetben az átlagos szabadenergia kiszámolható a rendszerre zárt alakban, két fizikailag értelems paraméterrel kifejezve: az egyik paraméter eredő mágnesezettség jellegű, a másik a mágnesezettség szórását jellemzi. A spinüveg helyzetnek az felel meg, amikor az eredő mágnesezettség eltűnik, de a szórás véges, szemben például a ferromágneses renddel, ahol az eredő mágnesezettség nem zérus.
egy véletlen valószínűségi változó Gauss-eloszlással. Ebben az esetben az átlagos szabadenergia kiszámolható a rendszerre zárt alakban, két fizikailag értelems paraméterrel kifejezve: az egyik paraméter eredő mágnesezettség jellegű, a másik a mágnesezettség szórását jellemzi. A spinüveg helyzetnek az felel meg, amikor az eredő mágnesezettség eltűnik, de a szórás véges, szemben például a ferromágneses renddel, ahol az eredő mágnesezettség nem zérus.
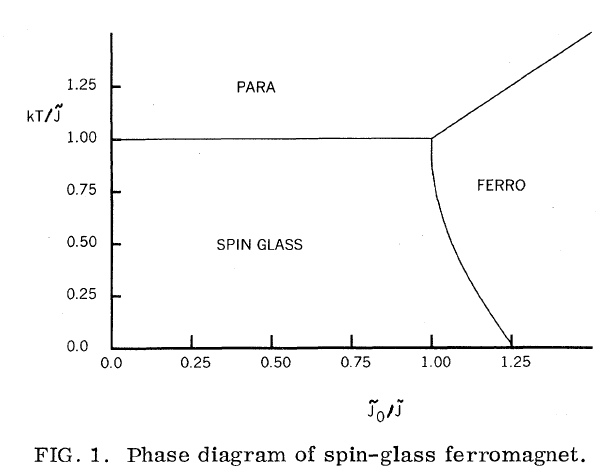
A fázisteret két paraméterrel lehet felmérni: a csatolás relatív szórásával (a fenti Gauss szórása osztva az átlaggal) valamint a csatolás szórásának és a hőmérsékleti energiának (kT) az arányával. Ezen a diagrammon a spinüveg fázis akkor jön létre, amikor a csatolás erősebb a hőmérsékleti fluktuációknál, de a relatív szórása nagy (Megyjegyzés: az ábra vízszintes tengelyén a relatív szórás reciproka van: az átlag osztva a szórással).
Markov-lánc, Markov-folyamatok
Egy sztochasztikus folyamatot jellemezhetünk azzal, hogy diszkrét időpillanatokban a tekintett valószínűségi változó milyen értékeket vett fel. Egy rendszert akkor tekintünk leírtnak, ha meg tudjuk mondani minden időpillanatra, minden értékre a megfelelő valószínűségeket:
ahol 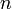 a leírni kívánt lépések száma. Mivel ez egy valószínűség, ezért minden
a leírni kívánt lépések száma. Mivel ez egy valószínűség, ezért minden 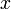 változójára kiintegrálva 1-et kell kapnunk, ez a norma-feltétel. Ezen felül, ha csak egy x változóra integrálunk, akkor az eggyel kisebb "rendű" valószínűségi kifejezést kell kapnunk:
változójára kiintegrálva 1-et kell kapnunk, ez a norma-feltétel. Ezen felül, ha csak egy x változóra integrálunk, akkor az eggyel kisebb "rendű" valószínűségi kifejezést kell kapnunk:
Tehát ha az egyik mintavételi időpontban minden lehetséges kimenetelre integrálunk, akkor olyan, mintha azt a pontot nem vennénk figyelembe. Ez a kompatibilitási feltétel.
Markov-folyamatoknál a rendszer jövőbeli állapotainak valószínűségét a korábbi, ismert állapotokból szeretnénk meghatározni. Ennek megfelelően ezt egy feltételes valószínűséggel fogalmazhatjuk meg:
azaz, ha ismert a rendszer vislkedése 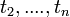 pillanatokban, akkor emellett a feltétel mellett milyen valószínűséggel lesz
pillanatokban, akkor emellett a feltétel mellett milyen valószínűséggel lesz 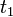 -ben
-ben 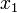 állapotban. Egy folyamat akkor Markov-folyamat, ha rendelkezik a Markov-tulajdonsággal, ami azt mondja, hogy a rendszer csak a legutóbbi állpotától függ:
állapotban. Egy folyamat akkor Markov-folyamat, ha rendelkezik a Markov-tulajdonsággal, ami azt mondja, hogy a rendszer csak a legutóbbi állpotától függ:
Ebből következik, hogyha 1 pontban ismert a Markov-folyamat, valamint az átmeneti valószínűségek, akkor teljes rendszer ismert, mert rekurzívan minden következő (vagy megelőző) állapot felírható az átmeneti valószínűségekkel:
Például ha egy diffúziós-folyamatot szeretnénk leírni, akkor az átmeneti valószínűség Gauss:
Homogénnek nevezzük a Markov-folyamatot, ha az átmeneti valószínűég időeltolás-invariáns:
Homogén diffúziós folyamatokra eben a kontextusban is levezethető a Fokker-Planck-egyenlet, ami lényegében a valószínűség-áramsűrűség megmaradását fejezi ki:
Brown-mozgás
Esetleg meg lehet említeni/felírni a Brown-mozgást, mint példát diszkrét Markov-folyamatra
Lásd még a Transzportfolyamatok tétel végét.