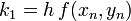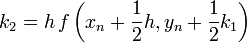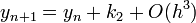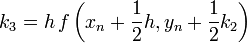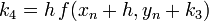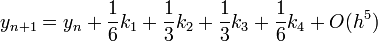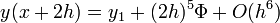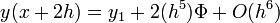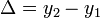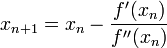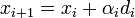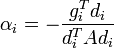„Numerikus módszerek” változatai közötti eltérés
a (→Konjugált gradiens módszer) |
a (→Konjugált gradiens módszer (iteratív változat)) |
||
| 106. sor: | 106. sor: | ||
===Konjugált gradiens módszer (iteratív változat)=== | ===Konjugált gradiens módszer (iteratív változat)=== | ||
| − | A konjugált gradiens módszer lineáris egyenletrendszert tud megoldani, abban az esetben, ha az együtthatómátrix szimmetrikus és pozitiv definit. | + | A konjugált gradiens módszer lineáris egyenletrendszert tud megoldani, abban az esetben, ha az együtthatómátrix szimmetrikus és pozitiv definit, ami sokszor fellép optimalizálási problémák vagy parciális differenciál egyenletek megoldásakor. A mátrix előbbi tulajdonságai szemléletesen annak felel meg, hogy egy olyan sokdimenziós potenciálban keresünk minimumot, amelynek nincs nyeregfelülete, hanem egyértelmű minimuma van. Legyen az egyenletrendszer: <math>Ax = b\,</math>. Belátható, hogy ennek a megoldása a fenti A-ra vonatkozó feltételek mellett minimalizálja a következő függvényt: |
:<math>f(x) = \frac{1}{2}x^T A x - x^T b\,</math>. | :<math>f(x) = \frac{1}{2}x^T A x - x^T b\,</math>. | ||
A lap jelenlegi, 2011. június 15., 13:44-kori változata
Tartalomjegyzék
Differenciálegyenlet-megoldó módszerek
A differenciálegyenlet-megoldó numerikus módszereknek alapvetően két különböző csoportjük van, az explicit és implicit módszerek.
Mindkét esetben arra keressük a választ, hogyha ismert a rendszer állapota egy 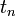 időpontban, valamint tetszőleges
időpontban, valamint tetszőleges 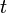 -re elő tudjuk állítani a deriváltakat, akkor mi a lehető legjobb becslés a rendszer jellemzőire (változóira) egy
-re elő tudjuk állítani a deriváltakat, akkor mi a lehető legjobb becslés a rendszer jellemzőire (változóira) egy 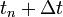 időpontban.
időpontban.
Explicit módszerek
Az explicit módszerek egy zártan kiértékelhető (értsd: behelyettesítesz és kész) alakot adnak az 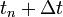 -beli értékekre egy, vagy néhány korábbi pontban ismert állapotokból, valamint az ott ismert deriváltakból.
-beli értékekre egy, vagy néhány korábbi pontban ismert állapotokból, valamint az ott ismert deriváltakból.
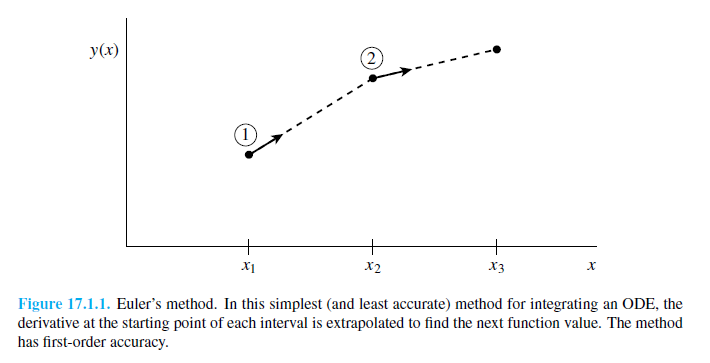
Euler-módszer
A legegyszerűbb egylépéses módszer. Az y(x=0)=y0 kezdőfeltétellel megadott, y’=f(x,y) diffegyenlet megoldása esetén az Euler lépés alakja (Taylor-sorfejtés első két tagja):
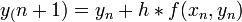
Hibája: Taylor-sorfejtést tovább írjuk, a különbség 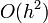 lesz. Használata nem javasolt, mert a hibák hamar felösszegződnek, a megoldás „felrobban”. Ennek elkerülésére érdemes lehet használni az implicit Euler-módszert:
lesz. Használata nem javasolt, mert a hibák hamar felösszegződnek, a megoldás „felrobban”. Ennek elkerülésére érdemes lehet használni az implicit Euler-módszert: 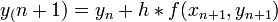 . Ez nagy h értékekre is stabil marad.
. Ez nagy h értékekre is stabil marad.
Runge-Kutta módszer
Miért használjuk? Mert sokkal pontosabb, mint az Euler-módszer.
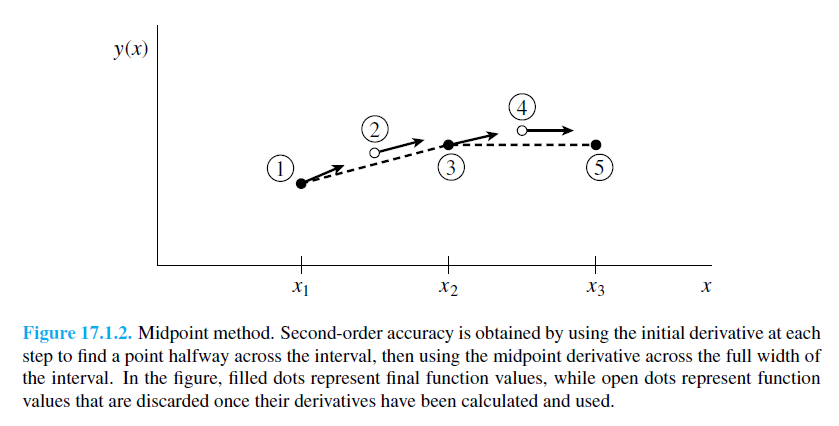
Másodrendű RK (vagy midpoint method - középponti módszer)
Ez a módszer tehát harmadrendig pontos. Általánosan az n-ed rendű RK-nak 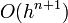 hibája van.
hibája van.
Negyedrendű RK
A negyedrendű módszerben négyszer kell kiértékelni az f függvényt, míg az Euler-módszernél egyszer kellett. Ezért ennek a használata akkor gazdaságos, ha ugyanakkora pontosság mellett legalább négyszer akkora lehet a lépésköz.
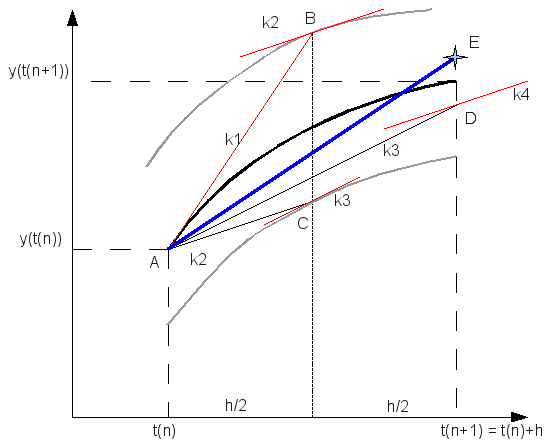
Adaptív RK
Egy differenciálegyenlet megoldása során lehetnek gyorsan és lassan változó szakaszok a függvényben. A lassan változó szakaszok integrálása során nagyobb lépéseket is tehetünk a hiba növekedése nélkül. Ennek a megoldására szolgál az adaptív Runge-Kutta módszer. Alapötlete, hogy egy lépést tegyünk meg egyszer teljesen (2h-val, 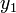 ), egyszer pedig két fél lépésben (h-val,
), egyszer pedig két fél lépésben (h-val, 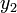 ). Mindegyik lépés 4 függvény kiértékelést igényel (3*4), de ebből kettő megegyezik, így 11 kiértékelés szükséges a 2*4 helyett, ami a két fél lépésből jönne össze.
). Mindegyik lépés 4 függvény kiértékelést igényel (3*4), de ebből kettő megegyezik, így 11 kiértékelés szükséges a 2*4 helyett, ami a két fél lépésből jönne össze.
A kettő közti különbség:
A különbség 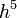 -nel skálázik. Ha egy
-nel skálázik. Ha egy 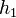 lépés eredménye
lépés eredménye 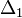 , és mi
, és mi 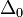 hibát akarunk elérni, akkor
hibát akarunk elérni, akkor 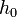 lépést kell tennünk, ami:
lépést kell tennünk, ami:
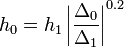
Ha 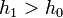 , akkor meg kell ismételni a számolást egy kisebb lépéssel, ha pedig
, akkor meg kell ismételni a számolást egy kisebb lépéssel, ha pedig 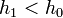 , akkor a következő lépésben használhatjuk
, akkor a következő lépésben használhatjuk 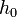 -t lépésként.
-t lépésként.
Implicit módszerek
Az implicit módszerek az eddigiekkel szemben más logikán alapszanak: tegyük fel, hogy a 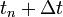 -pontban vagyunk, és ezzel fejezzük ki az itteni deriváltakat, és arra keressük a választ, hogy milyen értékeire az egyenletrendszernek leszünk konzisztensek a korábbi,
-pontban vagyunk, és ezzel fejezzük ki az itteni deriváltakat, és arra keressük a választ, hogy milyen értékeire az egyenletrendszernek leszünk konzisztensek a korábbi, 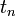 -beli értékekkel. Ez tehát egy bonyolultabb feladat, tipikusan egy egyenletrendszert kell megoldanunk minden lépésben, ami jobb esetben lineáris.
-beli értékekkel. Ez tehát egy bonyolultabb feladat, tipikusan egy egyenletrendszert kell megoldanunk minden lépésben, ami jobb esetben lineáris.
Miért érdekesek ezek a módszerek? Azért, mert sokkal stabilabbak (esetleg feltétel nélkül stabilak!), mint az explicit módszerek, ahol nem választhatunk akármekkora lépést, mert akkor a megoldás hasnzálhatatlan lesz (elszáll).
Egyenletrendszerek megoldása
Lineáris egyenletrendszernek nevezzük az olyan egyenletrendszert, melyben minden változó az első hatványon szerepel. Ezeket felírhatjuk mátrixformában is: 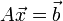 . Az A mátrixban tároljuk az egyenletrendszerben szereplő együtthatókat,
. Az A mátrixban tároljuk az egyenletrendszerben szereplő együtthatókat, 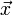 vektor az ismeretlenek vektora,
vektor az ismeretlenek vektora, 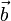 vektorban pedig az egyenletek jobb oldalainak értékei szerepelnek. Célunk meghatározni az
vektorban pedig az egyenletek jobb oldalainak értékei szerepelnek. Célunk meghatározni az 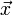 -t, ehhez beszorozzuk jobbról az előző egyenletet A-1-zel:
-t, ehhez beszorozzuk jobbról az előző egyenletet A-1-zel: 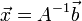 . A feladatunk tehát az A mátrix inverzét meghatározni.
. A feladatunk tehát az A mátrix inverzét meghatározni.
Gauss-Jordan elimináció
A Gauss-elimináció során az A mátrix és a 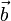 soraival egyszerre végzünk transzformációkat (másképp fogalmazva: az egyenleteket alakítjuk át). A megengedett transzformációk:
soraival egyszerre végzünk transzformációkat (másképp fogalmazva: az egyenleteket alakítjuk át). A megengedett transzformációk:
- mátrix két sorának felcserélése (két egyenlet cseréje)
- mátrix sorának számmal való szorzása
- a mátrix egy sorához egy másik skalárszorosának hozzáadása
A cél, hogy ilyen transzformációk sorozatának alkalmazásával A mátrixból egy felső háromszög mátrixok csináljunk. Ezután alulról fölfelé haladva behelyettesítéssel megkapjuk sorban 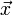 elemeit. Példa
elemeit. Példa
LU dekompozíció
Legyen A egy kvadratikus mátrix, erre az LU felbontás: A = LU. Az L és U mátrixok alsó illetve felső háromszög mátrixok (főátlóban is vannak elemek). Példa
Alkalmazása
- Determináns számolás: det(A) = det(L)*det(U)
- A háromszög mátrixok determinánsa a főátlóban lévő elemek szorzata, ezért ez nagyon egyszerűen számolható
- Mátrix inverz:
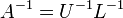
- Háromszög mátrix inverze könnyen számolható, ezért jó ez a felbontás.
Singular Value Decomposition - Szinguláris érték dekompozíció
Sokszor előfordul, hogy a mátrix, amit invertálni akarunk, közel van a szingulárishoz (det A ≈ 0), és sem a Gauss-elimináció, se az LU felbontás nem jár sikerrel.
Adott egy A mátrixunk, ami MxN méretű. Ezt a mátrixot felírhatjuk UWVT formában, ahol:
- U: MxN, oszlop-ortogonális mátrix
- W: NxN, diagonális, a szinguláris értékeket tartalmazza
- VT: NxN, ortogonális mátrix
A módszer segítségével nem-négyzetes mátrixokat is tudunk invertálni (pszeudoinverz) a következő módon:
![A^{-1} = V\,[diag(1/w_j)]\,U^T](/images/math/b/e/2/be29f4083659602a3acf54303900924a.png)
Ami problémát okozhat, az a szinguláris értékek reciproka, ha az nulla, vagy nagyon közel van nullához. A megoldás, hogy ebben az esetben az 1/wj-t nullának vesszük.
Optimalizációs módszerek - szélsőérték keresés
Newton-iteráció
Bár eredetileg a Newton-iterációt gyökkeresésre szokás alkalmazni, azonban ha ismert, vagy előállítható a függvény deriváltja, aminek a szélsőértékét keressük, akkor a derivált függvény zérushelye éppen a függvény szélsőértékét adja. A Newton-iteráció alakja szélsőérték keresésre:
ahol ' a deriválást jelöli. Látszik, hogy a második deriváltra is szükségünk van. A Newton-módszer kiterjeszthető többváltozó esetére is, ekkor az első deriváltak vektora és a második deriváltakat tartalmazó mátrixra van szükségünk az analóg formula kiértékeléséhez.
Konjugált gradiens módszer (iteratív változat)
A konjugált gradiens módszer lineáris egyenletrendszert tud megoldani, abban az esetben, ha az együtthatómátrix szimmetrikus és pozitiv definit, ami sokszor fellép optimalizálási problémák vagy parciális differenciál egyenletek megoldásakor. A mátrix előbbi tulajdonságai szemléletesen annak felel meg, hogy egy olyan sokdimenziós potenciálban keresünk minimumot, amelynek nincs nyeregfelülete, hanem egyértelmű minimuma van. Legyen az egyenletrendszer: 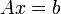 . Belátható, hogy ennek a megoldása a fenti A-ra vonatkozó feltételek mellett minimalizálja a következő függvényt:
. Belátható, hogy ennek a megoldása a fenti A-ra vonatkozó feltételek mellett minimalizálja a következő függvényt:
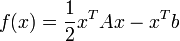 .
.
Vezessük be a konjugáltság fogalmát két vektorra:
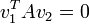 .
.
Ha 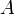
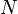 dimenziós, akkor létezik ennyi darab konjugált vektor (jelöljük
dimenziós, akkor létezik ennyi darab konjugált vektor (jelöljük 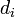 -vel), amelyek lineárisan függetlenek, tehát bázist alkotnak, ezért minden vektor kifejthető rajtuk, speciálisan a megoldás x is:
-vel), amelyek lineárisan függetlenek, tehát bázist alkotnak, ezért minden vektor kifejthető rajtuk, speciálisan a megoldás x is: 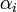 koefficiensekkel. Ezt behelyettesítve az egyenletrendszerbe kapjuk, hogy:
koefficiensekkel. Ezt behelyettesítve az egyenletrendszerbe kapjuk, hogy:
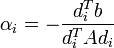 .
.
Tehát a cél ezek után 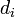 -k előállítása. Az ötlet az, hogy állítsuk elő sorban ezeket az irányokat, egyenként minimalizálva, egyre nagyobb altereiben A-nak. Konkrétan az állítás: a következő
-k előállítása. Az ötlet az, hogy állítsuk elő sorban ezeket az irányokat, egyenként minimalizálva, egyre nagyobb altereiben A-nak. Konkrétan az állítás: a következő 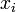 sorozat a megoldáshoz konvergál:
sorozat a megoldáshoz konvergál:
ahol a kifejtési együttható:
és:
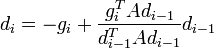 , de az első lépésben egyszerűen a legmeredekebb irányba lépünk:
, de az első lépésben egyszerűen a legmeredekebb irányba lépünk: 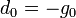
végül a gradiens irány egyszerűen a derivált kiértékelése:
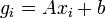 ,
,
Szemléletesen az történik, hogy ahányszor előállítunk egy a minimum felé mutató gradiens irányt, abból levonjuk a korábbi irányok konjugáció által definiált vetületét. Tehát minden lépésben egy irányban megkeressük az abban az irányban elérhető legjobb minimumot és a későbbi lépéseket úgy választjuk meg, hogy erre az irányra merőlegesek legyenek, így nem rontják el a korábban elért rész-minimumokat. Ebből az is látszik, hogyha mind az N irányban elvégeztük ezeket a lépéseket, akkor elvileg a minimumban kell lennünk (nincs több független irány, amiben lehetne minimumot keresni). A gyakorlatban a kerekítési hibák ebben megakadályoznak.
Szimulált hőkezelés
A módszer elnevezése az anyagtudomány területéről ered, ahol hőkezelési eljárásokkal lehet változtatni egy anyag kristályosodási méretét. Számítógépes módszerként egy sokdimenziós függvény energiaminimumának megkeresésére lehet használni.
Működési struktúra:
- Válasszunk egy tetszőleges kezdőállapotot (i)
- Válasszuk ki az egyik szomszédot (j)
- Ha a szomszéd energiája kisebb, átlépünk rá
- Ha nagyobb a szomszéd energiája, az energiakülönbség, és egy globális T paraméter által meghatározott valószínűség szerint elfogadjuk a nagyobb energiájú helyet
Az elfogadási valószínűségek tehát:
- ha f(j) ≤ f(i), akkor 1
- ha f(j) > f(i), akkor
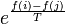
A T hőmérsékletet kezdetben nagynak választva, majd folyamatosan csökkentve ezzel a módszerrel megtalálhatjuk a függvény globális minimumát.