„Adatelemzés: bootstrap modellek '12” változatai közötti eltérés
(Új oldal, tartalma: „<!-- Ennek részletesen utána kell nézni a vmelyik adatos kövnyebn h mik tartoznak itt még egy témakörbe... ilyen adatújraosztásos, hibabecslős módszerek... úgy…”) |
|||
| 6. sor: | 6. sor: | ||
Egy ''X'' valószínűségi változó eloszlását különféle paraméterekkel jellemezhetjük: várható érték, szórás, ferdeség, stb. Ezeket a paramétereket egy ''n'' elemű minta alapján statisztikai függvények segítségével becsüljük. Pl.: a várható értéket a mintaátlaggal becsüljük, az empirikus és a korrigált empirikus szórás a szórás becslései. A becslésektől elvárjuk, hogy (legalább aszimptotikusan) torzítatlanok legyenek, valamint a becslés standard hibája a mintaszám növelésével nullához tartson. Ha kicsi a mintaszámunk, akkor nemcsak, hogy pontatlan lesz a becslésünk, de a pontosság jellemzőit sem tudjuk megbecsülni (pl.: konfidencia-intervallum) a klasszikus statisztika eszközeivel. | Egy ''X'' valószínűségi változó eloszlását különféle paraméterekkel jellemezhetjük: várható érték, szórás, ferdeség, stb. Ezeket a paramétereket egy ''n'' elemű minta alapján statisztikai függvények segítségével becsüljük. Pl.: a várható értéket a mintaátlaggal becsüljük, az empirikus és a korrigált empirikus szórás a szórás becslései. A becslésektől elvárjuk, hogy (legalább aszimptotikusan) torzítatlanok legyenek, valamint a becslés standard hibája a mintaszám növelésével nullához tartson. Ha kicsi a mintaszámunk, akkor nemcsak, hogy pontatlan lesz a becslésünk, de a pontosság jellemzőit sem tudjuk megbecsülni (pl.: konfidencia-intervallum) a klasszikus statisztika eszközeivel. | ||
| − | Mikor nevezhető kicsinek a mintaszám? Akkor, ha a becslés pontossági jellemzőinek (torzítás, standard hiba, konfidencia-intervallum) az ''n'' elemű mintából történő becslésekor indokolatlan a határeloszlásra való áttérés (a "klasszikus" képletek nem alkalmazhatók). A probléma megoldására találták ki az újra mintavételező | + | Mikor nevezhető kicsinek a mintaszám? Akkor, ha a becslés pontossági jellemzőinek (torzítás, standard hiba, konfidencia-intervallum) az ''n'' elemű mintából történő becslésekor indokolatlan a határeloszlásra való áttérés (a "klasszikus" képletek nem alkalmazhatók). A probléma megoldására találták ki az újra mintavételező módszereket |
==Bootstrap módszer== | ==Bootstrap módszer== | ||
| 51. sor: | 51. sor: | ||
Két modell összehasonlításához az így kapott négyzetes hibákat kell összehasonlítani, amelyikre kisebb, az jobban leírja az adatokat. | Két modell összehasonlításához az így kapott négyzetes hibákat kell összehasonlítani, amelyikre kisebb, az jobban leírja az adatokat. | ||
| + | |||
| + | ---- | ||
| + | Egyéb újra mintavételező technikák: [http://en.wikipedia.org/wiki/Resampling_%28statistics%29 Resampling (statistics)] (found by Adrian) | ||
{{MSc 2012 záróvizsga}} | {{MSc 2012 záróvizsga}} | ||
A lap 2012. június 13., 12:15-kori változata
Egy X valószínűségi változó eloszlását különféle paraméterekkel jellemezhetjük: várható érték, szórás, ferdeség, stb. Ezeket a paramétereket egy n elemű minta alapján statisztikai függvények segítségével becsüljük. Pl.: a várható értéket a mintaátlaggal becsüljük, az empirikus és a korrigált empirikus szórás a szórás becslései. A becslésektől elvárjuk, hogy (legalább aszimptotikusan) torzítatlanok legyenek, valamint a becslés standard hibája a mintaszám növelésével nullához tartson. Ha kicsi a mintaszámunk, akkor nemcsak, hogy pontatlan lesz a becslésünk, de a pontosság jellemzőit sem tudjuk megbecsülni (pl.: konfidencia-intervallum) a klasszikus statisztika eszközeivel.
Mikor nevezhető kicsinek a mintaszám? Akkor, ha a becslés pontossági jellemzőinek (torzítás, standard hiba, konfidencia-intervallum) az n elemű mintából történő becslésekor indokolatlan a határeloszlásra való áttérés (a "klasszikus" képletek nem alkalmazhatók). A probléma megoldására találták ki az újra mintavételező módszereket
Bootstrap módszer
Legyen X egy valószínűségi változó, 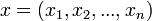 pedig egy n elemű minta X-re, s(x) pedig X valamely paraméterének becslése. A bootstrap-szimuláció során visszatevéssel egy új, szintén n elemű mintát veszünk:
pedig egy n elemű minta X-re, s(x) pedig X valamely paraméterének becslése. A bootstrap-szimuláció során visszatevéssel egy új, szintén n elemű mintát veszünk: 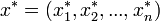 . Pl.: n=5-re:
. Pl.: n=5-re: 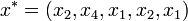 . Az x*-ra is alkalmazzuk s(x)-et, így s(x*)-ot kapjuk. Az eljárást N-szer megismételjük, így kapjuk s(x)-ek egy sorozatát:
. Az x*-ra is alkalmazzuk s(x)-et, így s(x*)-ot kapjuk. Az eljárást N-szer megismételjük, így kapjuk s(x)-ek egy sorozatát: 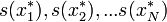 . Ha N elég nagy, akkor az s(x) becslés bootstrap-utánzatainak empirikus eloszlása jól modellezi az adott statisztika elméleti eloszlását.
. Ha N elég nagy, akkor az s(x) becslés bootstrap-utánzatainak empirikus eloszlása jól modellezi az adott statisztika elméleti eloszlását.
Jackknife módszer
Ha van egy n elemű mintánk, annak az átlagát 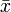 jelöli. Ugyanakkor kiszámolhatjuk az átlagot akkor is, ha a j-edik elemet kivágjuk (erre utal a módszer elnevezése is):
jelöli. Ugyanakkor kiszámolhatjuk az átlagot akkor is, ha a j-edik elemet kivágjuk (erre utal a módszer elnevezése is):
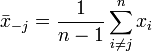
Vegyük észre, hogy ha ismert 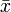 és
és 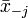 is, akkor ki tudjuk számolni xj-t:
is, akkor ki tudjuk számolni xj-t: 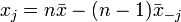
Tegyük fel, hogy az eloszlás egy 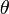 paraméterét akarjuk meghatározni. n pontra ennek a becslése:
paraméterét akarjuk meghatározni. n pontra ennek a becslése:
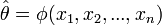
Az előző ötletet felhasználva 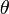 egy részleges becslését kapjuk, ha kivesszük a j-edik elemet:
egy részleges becslését kapjuk, ha kivesszük a j-edik elemet:
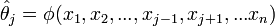
Szintén az előző ötlet alapján kiszámolhatjuk a j-edik pszeudoértéket:
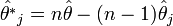
A fentiek alapján a 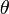 jackknife becslése:
jackknife becslése:
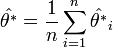
A 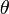 paraméter varianciáját a pszeudoértékekből becsülhetjük:
paraméter varianciáját a pszeudoértékekből becsülhetjük:
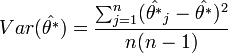
Cross-validation
A cross-validation egy olyan statisztikai módszer, melyben a rendelkezésre álló adatokat két csoportba osztjuk: egy tanító halmazra, amelyre az analízist végezzük, és egy teszt halmazra, amin kiértékeljük az analízis eredményét. A leginkább használt típusa a k-fold cross-validation, amiben az adatokat k darab, közel egyforma méretű csoportba osztjuk. A módszer k darab iterációt használ, és minden iterációban egy másik csoportot választunk tanító halmaznak, a többi pedig a teszt halmaz lesz. A leggyakoribb a k=10 eset.
A cross-validation-t kétféle célból használhatjuk:
- Megbecsüljük egy modell hatékonyságát a rendelkezésre álló adatokon
- Összehasonlítsunk két vagy több modellt, és eldöntsük, melyik írja le jobban az adatainkat
A módszer menete a következő (az i-edik iterációban, i = 1, ..., k):
- Az i-edik csoportra illesztjük a modellt (a modell lehet lineáris, polinom, stb.)
- A modellt alkalmazzuk a teszt halmazra, és kiszámítjuk az eltérést a modelltől (négyzetes hiba)
- i-t léptetjük
Két modell összehasonlításához az így kapott négyzetes hibákat kell összehasonlítani, amelyikre kisebb, az jobban leírja az adatokat.
Egyéb újra mintavételező technikák: Resampling (statistics) (found by Adrian)