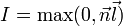Vizualizációs módszerek

Képalkotó módszerek

Ha 3D-s objektumokat szeretnénk megjeleníteni, valamennyire is kötődve a valóságos fényviszonyok reprodukálására, akkor alapvetően két fajta megközelítésből kell választanunk. Az egyik a fizikailag intuitív sugárkövetés alapú módszerek családja. Itt lényegében az intenzitást sugarak terjesztik az objektumok, így például a képernyőt reprezentáló kamera felületei között. A másik módszer, a raszterizáció eleve kihasználja, hogy a képet diszkrét pixelekből álló 2D-s rácson akarjuk előállítani és a problémát lényegében a felületek vetületeinek kitöltésére transzformálja.

Raszterizáció

Legyenek adottak a felületek, amelyeket le szeretnénk rajzolni a képernyőre. Ez nyilvánvalóan tartalmaz egy vetítést a 3D-s térből a 2D-s képfelületre. Ezt a lépést a raszterizáció a felületek (tipikusan poligonok) analitikus transzformációjával állítja elő. Poligonok esetén ez a csúcspontok levetítését jelenti. Ezek után két feladat van: előállítani pixelere diszkretizált képfelületen az alakzat körvonalát, majd kitölteni azt.

Négyzetrácsos képsík esetén mindkét feladat igen hatkékony algoritmusokkal valósítható meg. Az alakzat körvonalának előállítására a legegyszerűbb módszer a Bresemham-approximáció. Ez megadott két pont között sorban bejárja azokat a pixeleket, amelyeken a vonal áthalad. Az eljárás lényege, hogy a kindulási pontnak megfelelő pixelnél inicializál egy hiba változót, amit az egyenes meredekségének megfelelő értékkel növel. Amikor ez a hiba eléri azt a küszöböt, amikor az egyenes már a másik pixelhez van közelebb, akkor eggyel növeli az aktuális koordinátát és csökkenti a hibát. Az eljárás előnye, hogy lebegőpontos műveletek nélkül mnegvalósítható, olyan hatékonyan, hogy a belső ciklus léptetése csupűán néhány órajelet igényel.

Az alakzat körvonala után annak kitöltése úgy történhet, hogy meghatározzuk körvonal befoglaló téglalapját, és minden sorban a befoglaló széléről elindulva megnézzük, hogy mikor érünk el a körvonalhoz tartozó (előre megjelölt) pixelt. Ekkortól minden pixelt kitöltünk addig, amíg újra egy eleve már megjelölt pixelhez nem értünk.

A raszterizációs módszerek valóságot imitáló trükkjei ott jelennek meg, hogy milyen színértékeket rendelünk a kitöltés során a pixelekhez. Mivel poligonjaink vannak, ezek mindig háromszögekre bonthatóak (sőt, eleve így vannak tárolva). Minden a fényhatásokat jellemző paramétert a háromszögek csúcsaiban szokás eltárolni (a pozíción túl a felületi normális, adott pont beli szín, felületi textúra koordináta stb.), majd ezeket az értékeket interpolálni a háromszög felületén az aktuális kitöltési pontokra.

Igen egyszerű példaként, tekintsük a legegyszerűbb megvilágítást: ha egy háromszög a pontszerű fényforrás felé néz, akkor világosabb, ha elfele, akkor sötétebb. A legegyszerűbb esetben ezt a fényforrás irányának (l) és a felületi normálisnak (n) az irányával lehet elérni, Így az adott pixel intenzitás értéke a két normálvektor skalárisszorzata:

$I = \mathrm{max}(0, \vec{n}\vec{l})$

ahol a skalárisszorzat negatív lenne, ott zérus lesz a megvilágítás és így az intenzitás is.

Sugárkövetés

A sugárkövetés a teljes megjelenítést a reprezentálni kívánt 3D-s rendszer koordinátarendszerében végzi, nem a képernyő terében, mint a raszterizáció. Bár a sugárkövető algoritmusoknak igen széles palettája van, a közös pont az, hogy valamilyen sugarakat használnak a fényesség transzportjának leírására a felületek és testek között. Az alábbiakban a legegyszerűbb és legintuitívabb eljárást ismertetjük.

Tekintsük a klasszikus optikát motivációnak: adottak fényforrásaink, ahonnan fotonok indulnak ki, amik egyenes vonalban terjednek addig, amíg valamilyen felületet el nem érnek. A felületen a tükröződés és törés törvényeinek megfelelően megváltoznak, majd haladnak tovább a következő felület felé. Mindegyik ilyen sugarat jellemezhetünk az általa szállított fényességgel, illetve hullámhosszal, de a legegyszerűbb esetben számolhatunk RGB intenzitásokkal is.

A legegyszerűbb sugárkövetési eljárás tehát úgy állítja elő a képet, hogy követi a fényforrásokból induló sugarakat egészen addig, amíg azok el nem nyelődnek valahol. Az elnyelő objektunok közül kitüntetett a kékpernyőt reprezentáló test: az ide eső sugarak alkotják a végén megjelenő képet.

Mivel a sugarak kontinuum kezelése lehetetlen a változatos alakú testek és határfelületek miatt, ezért lényegében egy hatalmas méretű Monte-Carlo eljárással van dolgunk: nagyon sok fénysugarat indítunk és a képernyőn integráljuk a beeső intenzitást. Ebből azonnal következik sokminden, a legfontosabb, hogy a fénysugarak számával csak lassan nő a képminőség, eleinte igen zajos.

A sugárkövető algoritmusoknak azonban határozott előnyeik vannak a raszterizációs technikákkal szemben: az átlátszó, áttetsző, illetve nagyon sok tükröző felületet tartalmazó rendszerek kirajzolása raszterizációs módszerrel igen bonyolult, ezzel szemben sugárkövetéssel teljesen intuitív a megvalósításuk. Hasonlóan, a fizikailag korrekt képalkotás (pl. diszkrét színek helyett spektrumokkal számolás és csak a legvégén RGB konverzió) is jól illik ehhez a megközelítéshez. A növekvő számítási kapacitás, valamint a kiterjedt optimalizációs trükkök segítségével manapság már ez a módszer is általánosan használható, főleg ha a képminőség az elsődleges.

Színek reprezentálása

Amit a szemünkkel különböző színeknek látunk, az a fizikailag az elektromágneses sugárzás intenzitás spektruma. A szemünkben három színérzékeny receptor-rendszer található, amelyek körülbelül a vörös-zöld-kék színekre érzékenyek, azonban ez az érzékenység nem diszkrét frekvenciát jelent, hanem egy kiterjedt tartományt. Nagyon durván mondhatjuk azt, hogy a szem érzékenysége a három színre három Gauss-függvénnyel jellemezhető.

Ha a azt akarjuk leírni, hogy mekkora intenzitású választ vált ki egy adott spektrum a három érzékelő-rendszerben, akkor az matematikailag a három súlyfüggvénnyel való konvolúciját jelenti a spektrummnak. Ez a három szám feleltethető meg a technikában használatos RGB koordinátáknak.

Számos probléma van itt azonban: a szem eltérően érzékeny a három tartományban érkező intenzitásra, maga az érzékelés tipikusan logaritmikus. A legnagyobb probléma, hogy a súlyfüggvények nem egészen ismertek, sőt, nem is teljesen pozitív definitek (azaz bizonyos frekvencián érkező sugárzás blokkoló hatás fejt ki egyik, vagy másik receptorokon), így a pusztán három számmal történő reprezentációban számos egyszerűsítő feltevés van, amelyek bizonyos helyzetekben problémákhoz vezethetnek.