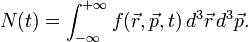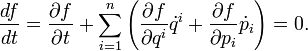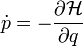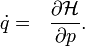„Soktest rendszerek” változatai közötti eltérés
(→Soktestrendszerek kontinuum leírása) |
|||
| 4. sor: | 4. sor: | ||
Amikor nagyon sok részecskének a jellemzőit kell leírni, akkor célszerű mindent sűrűségfüggvényekkel (ill. másnéven eloszlásfüggvényekkel) kifejezni. A súrúségfüggvény felintegrálva részecskeszámot ad, speciálisan, ha <math>N</math> részecskénk van a teljes vizsgált térben, akkor: | Amikor nagyon sok részecskének a jellemzőit kell leírni, akkor célszerű mindent sűrűségfüggvényekkel (ill. másnéven eloszlásfüggvényekkel) kifejezni. A súrúségfüggvény felintegrálva részecskeszámot ad, speciálisan, ha <math>N</math> részecskénk van a teljes vizsgált térben, akkor: | ||
| − | :<math>N = \int_{-\infty}^{+\infty} f(\vec{r}, \vec{p}, t) \, d^3 \vec{r} \, d^3 \vec{p}.</math> | + | :<math>N(t) = \int_{-\infty}^{+\infty} f(\vec{r}, \vec{p}, t) \, d^3 \vec{r} \, d^3 \vec{p}.</math> |
| + | A sűrűségfüggvény megváltozásának leírásához valamilyen mozgásegyenletre van szükségünk. A legegyszerűbb és egyben legáltalánosabb ilyen egyenlet a Liouville-egyenlet: | ||
| + | :<math>\frac{d f}{dt}= | ||
| + | \frac{\partial f}{\partial t} | ||
| + | +\sum_{i=1}^n\left(\frac{\partial f}{\partial q^i}\dot{q}^i | ||
| + | +\frac{\partial f}{\partial p_i}\dot{p}_i\right)=0.</math> | ||
| + | |||
| + | Itt <math>i</math> indexeli az <math>n</math> darab részecskét. Itt <math>q</math> a kanonikus koordináta, <math>p</math> a konjugált impulzus és az időderiváltakat a szokásos módon a Hamilton operátor adja: | ||
| + | |||
| + | :<math>\dot p = -\frac{\partial \mathcal{H}}{\partial q}</math> | ||
| + | :<math>\dot q =~~\frac{\partial \mathcal{H}}{\partial p}.</math> | ||
| + | |||
| + | Fontos kiemelni, hogy a Liouville-egyenlet egy 6n dimenziós egyenlet (szemben a későbbiekkel). Tömören megfogalmazva a fázistérfogat megmaradását fejezi ki a mozgás trajektóriája mentén. | ||
== Elektromágnesesen kölcsönható soktestrendszerek == | == Elektromágnesesen kölcsönható soktestrendszerek == | ||
A lap 2011. június 10., 15:41-kori változata
Az alábbiakban összefoglaljuk a sok részecskét tartalmazó statisztikus rendszerek leírására szolgáló egyenleteket, továbbá néhány fontos alkalmazást is megemlítünk. Ezekből az egyenleteből származtatható további eredmények pedig a Transzportfolyamatok tételben kerülnek kifejtésre.
Tartalomjegyzék
Soktestrendszerek kontinuum leírása
Amikor nagyon sok részecskének a jellemzőit kell leírni, akkor célszerű mindent sűrűségfüggvényekkel (ill. másnéven eloszlásfüggvényekkel) kifejezni. A súrúségfüggvény felintegrálva részecskeszámot ad, speciálisan, ha 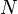 részecskénk van a teljes vizsgált térben, akkor:
részecskénk van a teljes vizsgált térben, akkor:
A sűrűségfüggvény megváltozásának leírásához valamilyen mozgásegyenletre van szükségünk. A legegyszerűbb és egyben legáltalánosabb ilyen egyenlet a Liouville-egyenlet:
Itt 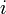 indexeli az
indexeli az 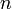 darab részecskét. Itt
darab részecskét. Itt 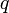 a kanonikus koordináta,
a kanonikus koordináta, 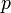 a konjugált impulzus és az időderiváltakat a szokásos módon a Hamilton operátor adja:
a konjugált impulzus és az időderiváltakat a szokásos módon a Hamilton operátor adja:
Fontos kiemelni, hogy a Liouville-egyenlet egy 6n dimenziós egyenlet (szemben a későbbiekkel). Tömören megfogalmazva a fázistérfogat megmaradását fejezi ki a mozgás trajektóriája mentén.