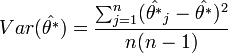„Adatelemzés: bootstrap modellek” változatai közötti eltérés
| 12. sor: | 12. sor: | ||
==Jackknife módszer== | ==Jackknife módszer== | ||
| + | Ha van egy ''n'' elemű mintánk, annak az átlagát <math>\bar{x}</math> jelöli. Ugyanakkor kiszámolhatjuk az átlagot akkor is, ha a ''j''-edik elemet kivágjuk (erre utal a módszer elnevezése is): | ||
| + | |||
| + | <math>\bar{x}_{-j} = \frac{1}{n-1} \sum_{i \neq j}^n x_i</math> | ||
| + | |||
| + | Vegyük észre, hogy ha ismert <math>\bar{x} \text{és} \bar{x}_{-j}</math> is, akkor ki tudjuk számolni x<sub>j</sub>-t: <math>x_j = n \bar{x} - (n-1) \bar{x}_{-j}</math> | ||
| + | |||
| + | Tegyük fel, hogy az eloszlás egy <math>\theta</math> paraméterét akarjuk meghatározni. ''n'' pontra ennek a becslése: | ||
| + | |||
| + | <math>\hat{\theta} = \phi (x_1, x_2, ..., x_n)</math> | ||
| + | |||
| + | Az előző ötletet felhasználva <math>\theta</math> egy részleges becslését kapjuk, ha kivesszük a ''j''-edik elemet: | ||
| + | |||
| + | <math>\hat{\theta}_j = \phi (x_1, x_2, ..., x_{j-1}, x_{j+1}, ... x_n)</math> | ||
| + | |||
| + | Szintén az előző ötlet alapján kiszámolhatjuk a ''j''-edik ''pszeudoértéket'': | ||
| + | |||
| + | <math>\hat{\theta^*}_j = n \hat{\theta} - (n-1) \hat{\theta}_j</math> | ||
| + | |||
| + | A fentiek alapján a <math>\theta</math> jackknife becslése: | ||
| + | |||
| + | <math>\hat{\theta^*} = \frac{1}{n} \sum_{i=1}^n \hat{\theta^*}_i</math> | ||
| + | |||
| + | A <math>\theta</math> paraméter varianciáját a pszeudoértékekből becsülhetjük: | ||
| + | |||
| + | <math>Var(\hat{\theta^*}) = \frac{\sum_{j=1}^n (\hat{\theta^*}_j - \hat{\theta^*} )^2}{n(n-1)}</math> | ||
==Cross-validation== | ==Cross-validation== | ||
A lap 2011. június 12., 13:26-kori változata
Egy X valószínűségi változó eloszlását különféle paraméterekkel jellemezhetjük: várható érték, szórás, ferdeség, stb. Ezeket a paramétereket egy n elemű minta alapján statisztikai függvények segítségével becsüljük. Pl.: a várható értéket a mintaátlaggal becsüljük, az empirikus és a korrigált empirikus szórás a szórás becslései. A becslésektől elvárjuk, hogy (legalább aszimptotikusan) torzítatlanok legyenek, valamint a becslés standard hibája a mintaszám növelésével nullához tartson. Ha kicsi a mintaszámunk, akkor nemcsak, hogy pontatlan lesz a becslésünk, de a pontosság jellemzőit sem tudjuk megbecsülni (pl.: konfidencia-intervallum) a klasszikus statisztika eszközeivel.
Mikor nevezhető kicsinek a mintaszám? Akkor, ha a becslés pontossági jellemzőinek (torzítás, standard hiba, konfidencia-intervallum) az n elemű mintából történő becslésekor indokolatlan a határeloszlásra való áttérés (a "klasszikus" képletek nem alkalmazhatók). A probléma megoldására találták ki az újra mintavételező módzsereket
Bootstrap módszer
Legyen X egy valószínűségi változó, 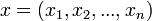 pedig egy n elemű minta X-re, s(x) pedig X valamely paraméterének becslése. A bootstrap-szimuláció során visszatevéssel egy új, szintén n elemű mintát veszünk:
pedig egy n elemű minta X-re, s(x) pedig X valamely paraméterének becslése. A bootstrap-szimuláció során visszatevéssel egy új, szintén n elemű mintát veszünk: 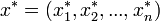 . Pl.: n=5-re:
. Pl.: n=5-re: 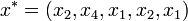 . Az x*-ra is alkalmazzuk s(x)-et, így s(x*)-ot kapjuk. Az eljárást N-szer megismételjük, így kapjuk s(x)-ek egy sorozatát:
. Az x*-ra is alkalmazzuk s(x)-et, így s(x*)-ot kapjuk. Az eljárást N-szer megismételjük, így kapjuk s(x)-ek egy sorozatát: 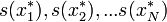 . Ha N elég nagy, akkor az s(x) becslés bootstrap-utánzatainak empirikus eloszlása jól modellezi az adott statisztika elméleti eloszlását.
. Ha N elég nagy, akkor az s(x) becslés bootstrap-utánzatainak empirikus eloszlása jól modellezi az adott statisztika elméleti eloszlását.
Jackknife módszer
Ha van egy n elemű mintánk, annak az átlagát 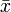 jelöli. Ugyanakkor kiszámolhatjuk az átlagot akkor is, ha a j-edik elemet kivágjuk (erre utal a módszer elnevezése is):
jelöli. Ugyanakkor kiszámolhatjuk az átlagot akkor is, ha a j-edik elemet kivágjuk (erre utal a módszer elnevezése is):
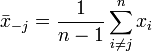
Vegyük észre, hogy ha ismert 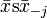 is, akkor ki tudjuk számolni xj-t:
is, akkor ki tudjuk számolni xj-t: 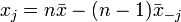
Tegyük fel, hogy az eloszlás egy 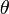 paraméterét akarjuk meghatározni. n pontra ennek a becslése:
paraméterét akarjuk meghatározni. n pontra ennek a becslése:
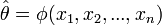
Az előző ötletet felhasználva 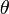 egy részleges becslését kapjuk, ha kivesszük a j-edik elemet:
egy részleges becslését kapjuk, ha kivesszük a j-edik elemet:
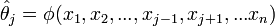
Szintén az előző ötlet alapján kiszámolhatjuk a j-edik pszeudoértéket:
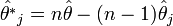
A fentiek alapján a 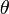 jackknife becslése:
jackknife becslése:
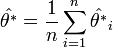
A 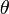 paraméter varianciáját a pszeudoértékekből becsülhetjük:
paraméter varianciáját a pszeudoértékekből becsülhetjük: