Dinamikai rendszerek, kaotikus viselkedés
Tartalomjegyzék
Dinamikus rendszerek elmélete
A dinamikai rendszerek elmélete csatolt differenciálegyenletek tulajdonságával foglalkozik, amiknek az időfejlődését néhány paraméter határozza meg. A rendszer időfejlődésének vizsgálata a paraméterek állapotterében zajlik.
Alapfogalmak
Fixpont és határciklus
Fixpontnak azt nevezzük, amikor a rendszer hosszú idő után a fázistér egy pontjában található meg. A fixpont lehet stabil (kis kitérésre visszatér), és instabil (kis kitérésre nem tér vissza). A határciklus a fázistérben egy zárt trajektória, amin a rendszer az idő előrehaladtával körbejár. Szintén lehet stabil vagy instabil.
Bifurkáció
Bifurkációról akkor beszélünk, amikor egy külső paraméter hatására a rendszer hosszú távú viselkedése kvalitatívan megváltozik (pl.: 1 fixpont → 2 fixpont, fixpont → határciklus, stb.)
Poincaré-metszet
A rendszer időfejlődését, főleg ha az d>3 dimenziós, nagyon nehéz grafikusan ábrázolni. Ezért a fázistérnek és egy síknak a metszetét vizsgáljuk. Ha egy közel periodikus pálya metszi a síkot (a fázistér egy alterét), akkor egy periódusidő múlva újra metszeni fogja, közel az előző ponthoz. Belátható, hogy egy pálya akkor periodikus, ha a Poincaré-metszetnek fixpontja.
Ljapunov-exponens
A Ljapunov-exponenssel az számszerűsíthetjük, hogy a fázistérben két közeli trajektória milyen gyorsan távolodik egymástól. Ha kezdetben 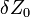 távolságra voltak, akkor az időben a távolságuk
távolságra voltak, akkor az időben a távolságuk 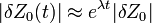 szerint növekszik (vagy csökken, ha
szerint növekszik (vagy csökken, ha 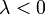 ).
).
Determinisztikus káosz
Káosz disszipatív rendszerekben
Diffúzió
Ismét sokadszorra:)