Vizualizációs módszerek '12

Bevezetés

A tudományos életben elsősorban a számolásaink numerikus eredményére vagyunk kíváncsiak, amiket jól definiált módszerekkel származtatunk a kérdéses rendszer számszerű értékeiből. Az efféle visszajelzéseket egyszerű parancssoros környezetben is megkaphatjuk, azonban több okból lehetünk kíváncsiak egy ennél intuitívabb reprezentációjára az adatainknak:

- Egy grafikon többet mond ezer szónál: Dinamika, vagy függvények diszkrét mintavételezésénél a görbe egy vizuális reprezentációja sokkal többet mond el, mint a puszta függvényértékek.

- Hibakeresés: Könnyen előfordulhat, hogy a numerikus értékek jónak tűnnek, ám amiből származnak mennyiségek teljesen hibásak. Szemléletes példa lehet erre fehérjekonformáció, ahol az energia elérhet egy minimumot úgy is, hogy közben lehetetlen módon tekeri fel az algoritmusunk a fehérjét.

- Emberi intuíció: Az emberi agy, mint célhardver rendkívül hatékonyan klaszterez, mintailleszt, élkiemel, stb. aminek két előnye is van. Egyfelől egyszerű ránézésre is ötletet adhat nekünk, hogy az adatokon elvégezzük ezen műveletek numerikus változatát, feltérképezve a lehetőségét mögöttes szabályoknak, másfelől "igazolhatjuk" a numerikus számításaink relevanciáját.

Képalkotási eljárások

Minket elsősorban a tudományos vizualizáció fog érdekelni, így a digitális képalkotás három fő ágazatát is ilyen szemszögből tárgyaljuk.

Digitális festészet

A digitális festészetet gyakran nem sorolják a digitális képalkotási módok közé, pedig nem kevés mozzanatában támaszkodik a számítógép képességeire. Ezen eljárás során a művész egérrel, esetlegesen érintőpanellel és tollal rajzol egy virtuális vászonra, amit aztán megszámlálhatatlan numerikus eljárással módosíthat igényei szerint. Ezáltal olyan látványelemeket is teremthet, amit kézzel, valódi ecsettel nem tudna reprodukálni, azonban tisztában van vele, hogy milyen egyszerű eljárások léteznek, amikkel egy lerajzolható alakzatot át tud vinni egy olyanba, amit ő elképzelt. A film- és játékipar támaszkodik döntőrészben erre az eljárásra, ahol látványterveket, grafikákat, forgatókönyvet, vagy éppen egészestés filmeket készítenek ilyen eljárásokkal. Tudományos célokra nehezen használható. Legközelebbi alkalmazása az ilyen célokra használt programok képjavítási és transzformációs képességei, amivel pl. csillagászok végezhetnek utómunkálatokat teleszkóp felvételeken. Ezekben a szoftverekben színszűrős képeket komponálni vagy éppen dekomponálni, a lehető legkevesebb torzióval forgatni, nagyítani, élesíteni pár kattintásba kerül csupán.

Sugárvetés és sugárkövetés

A sugárkövetés az előzőnél már közelebb áll tudományhoz. A digitális festészetnél ugyan szintén szerepe volt a vászon méretének, mint ahogy a képpontjai számának is, azonban a sugárkövetésben centrális fontosságú a vászon jellege. Azt tudjuk, hogy a szemünkbe úgy jut a el a világ képe, hogy különböző fényforrásokból fotonok lépnek ki, majd ezek különböző felületekről visszaverődve, vagy áthaladva rajtuk veszítenek energiájukból, változik az energiájukhoz tartozó hullámhossz, változik a színük (emberi léptékkel eltekinthetünk a megtett táv szerinti intenzitáscsökkenéstől, egyelőre). Ezek a fotonok össze-vissza pattognak a világban, mígnem egy részük eljut a szemünkbe. A sugárkövetés ugyanezt a folyamatot követi végig, a monitoron lévő pixelek három hullámhosszán, megnézve, hogy ilyen hullámhosszokon mennyi energiája marad azoknak a fotonoknak, amik a virtuális színterünkben a fényforrásokból eljutnak a kamerába.

Ahhoz, hogy meghatározzuk egy pixel színét a képernyőn, egy sugarat bocsátunk a színterünkbe, és kiszámítjuk annak színét az árnyalási egyenlet kiszámításával, ami az

$L(\mathbf{x},\mathbf{\omega})=L_e (\mathbf{x},\mathbf{\omega}) + \int L(h(\mathbf{x},-\mathbf{\omega'}),\mathbf{\omega'}) f_r (\mathbf{\omega'},\mathbf{x},\mathbf{\omega})(-\mathbf{\omega'}\cdot \mathbf{n} )) \mathrm{d\mathbf{\omega'}}$

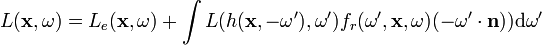
alakot ölti. Az egyenletben 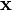$\mathbf{x}$ jelöli a 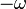$-\mathbf{\omega}$ irányba induló sugár a kamerához legközelebb eső metszéspontját a színtér objektumain. Ennek a felületelemnek az ebből az irányból nézett 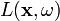$L(\mathbf{x},\mathbf{\omega})$ sugársűrűsége egyenlő lesz az 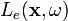$L_e (\mathbf{x},\mathbf{\omega})$ , a felületi pontból a kamera irányába sugárzott radiancia, avagy a felület saját emissziója, továbbá az erre a felületelemre máshonnan érkező sugársűrűség súlyozva azzal a valószínűséggel, hogy épp abba a nézeti irányba verődnek vissza, és megszorozva a 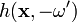$h(\mathbf{x},-\mathbf{\omega'})$ láthatósági lépcsőfüggvénnyel. Ezt a súlyfaktort jelöljük 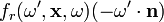$f_r (\mathbf{\omega'},\mathbf{x},\mathbf{\omega})(-\mathbf{\omega'}\cdot \mathbf{n} )$ –nel, ahol 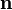$\mathbf{n}$ az aktuális felületelem normálisa. Az 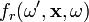$f_r (\mathbf{\omega'},\mathbf{x},\mathbf{\omega})$ függvényt kétirányú visszaverődési eloszlási függvény (angol szakirodalomban BRDF, avagy Bi-directional Reflection Distribution Function) néven szokás említeni, aminek a meghatározása egy bizonyos anyagra több ezer mérési pontból történik műszerek által. Mivel ez a fajta meghatározás rendkívül költséges és időigényes, így fenomenologikus modelleket szoktak alkalmazni helyette. Az egyenlet legszámításigényesebb része a legközelebbi metszéspont megtalálása, illetve a takarási probléma megoldása, amiben egyenes-sík metszeteket kell keresni.

Fontos megjegyezni, hogy ezt az egyenletet az anyagok diszperziója miatt több hullámhosszon kell kiértékelni. Ezt a három hullámhosszt a szemünkben található csapok elnyelési maximumaira szokás venni, azonban ez gyakran nem esik egybe a monitorokban található pixelek fényének hullámhosszaival. A kettő közötti korrekciót hívják színleképezésnek (angolul tone mapping).

A sugárkövetés önmagában egy rekurzív eljárás, hiszen az egy pontba bocsátott sugarak után felösszegezzük, hogy más irányokból mennyi fény érkezik oda, azonban az ezekbe a felületelemekbe érkező fényt szintén ki kell számolni, és így tovább. A rekurziót csak addig érdemes folytatni, míg a többszöri visszaverődés után (ami függ az eltalált felületek minőségétől) még érdemi járulékot hordoz a pixel végső szín értékéhez. A rekurzió nélküli módszert szokás sugárvetésnek hívni. Sugárkövetést alkalmaznak stúdiók animációs filmek készítéséhez, ahol a színtér elemeit modellezéssel foglalkozó digitális művészek állítják elő, majd számítógépek renderelik le a képeket sugárkövetéssel.

Tudományos vizualizáció szempontból a sugárkövetés szükségtelenül költséges eljárás, azonban a sugárvetést gyakran alkalmazzák térfogati adatok megjelenítésére, például az orvostudományban. Ahol térfogati adatokat szeretnénk megjeleníteni, ott a kamera pozíciójából bocsátunk sugarakat a képernyő pixelein keresztül, majd ezeket a sugarakat követjük, hogy a térfogaton áthaladva az egyes hullámhosszokon mennyi energiát veszítenek. Ezáltal ahol hosszabb utat tesz megy egy sugár a térfogaton keresztül, ott nagyobb változást fog elszenvedni, mint ott ahol ritkább közegen keresztül haladnak át a sugarak, vagy ahol rövidebb utat tesznek meg a térfogatban.

Inkrementális képszintézis

Tudományos vizualizáció céljából az olyan megjelenítési eljárásokat kedveljük, ami a lényegi információt eljuttatja hozzánk, és emellett a lehető legkevesebb erőforrást emészti fel. Az erőforrás igény csökkentése vagy az interaktivitást növeli (vagy éppen teszi lehetővé), vagy a szükséges hardver költségét csökkenti. A számítógépes játékokban alkalmazott képszintézis egészen más a korábban említett kettőtől, és ennek a hardveres gyorsítására jöttek létre a grafikus kártyák, amik több olyan célirányos feldolgozót tartalmaznak, amik ennek az eljárásnak gyorsítják egyes lépéseit.

Az inkrementális képszintézis során nem azt vizsgáljuk, hogy mely fénysugarak jutnak el a szemünkbe, hanem hogy a színtér elemei, még pontosabban azok primitívei (vonalak és sokszögei) mely pixelekbe képződnek le a monitoron. Ez a raszterizáció lépése. Majd a raszterizációból kapott fragmentekről eldöntjük melyik van a legközelebb a kamerához (ergo nincs takarásban), majd eztán határozzuk meg az adott felületelem színét. A módszer alapelemei itt nagyobb építőkövek, a pixelek helyett primitívből állnak. Jellemzően sokkal kevesebb van egy színtérben, mint pixelből egy képernyőn. A metszési problémát is elkerüljük, cserébe viszont a takarási problémát kell megoldanunk. Míg sugárkövetésnél ingyen megkaptuk a tükröződések és árnyékolások eredményét, itt erre külön algoritmusokat kell kifejleszteni. Jellemzően ezek pótlására nem szín értékeket tartalmazó textúrákat alkalmaznak. Árnyékot számolhatunk úgy, hogy készítünk egy képet a fényforrás szemszögéből a színtérről, és azon pixeleknek megfelelő textúra koordinátákba írunk, amelyek látszódtak a fényforrás szemszögéből. Amikor a megfigyelő szemszögéből nézzük a színterünket, akkor ezeket a textúrákat használva tudhatjuk meg, hogy az adott felületelemekre jut-e fény a kérdéses fényforrásból. (Látható azonban, hogy ezzel a módszerrel még mindig nem kapunk sem tükröződést, sem diffúz felületekről érkező járulékos intenzitást.) A valós fényjelenségek reprodukálásának nehézségei ellenére, a megfelelő célhardverrel kellően realisztikus képeket lehet, interaktív sebességben előállítani.

Ugyan tudományos alkalmazásokban az esztétikum a legkevésbé fontos, ezért nincs is szükségünk nagyon költséges trükkök alkalmazására, azonban ezek minimális megléte igenis serkenti az agyunk megfelelő részeit, és a valósághű árnyékok és fényvisszaverődések segítenek a térérzet kialakításában, vagy éppen a felület irányának érzékeltetésében.

Mindazonáltal az inkrementális képszintézisben alkalmazott matematika, valamint a célzott hardver ismerete elengedhetetlen fontosságú, hogy hatékony megjelenítést tudjunk írni programjainkhoz.

Színek reprezentálása

Amit a szemünkkel különböző színeknek látunk, az a fizikailag az elektromágneses sugárzás intenzitás spektruma. A szemünkben három színérzékeny receptor-rendszer található, amelyek körülbelül a vörös-zöld-kék színekre érzékenyek, azonban ez az érzékenység nem diszkrét frekvenciát jelent, hanem egy kiterjedt tartományt. Nagyon durván mondhatjuk azt, hogy a szem érzékenysége a három színre három Gauss-függvénnyel jellemezhető.

Ha a azt akarjuk leírni, hogy mekkora intenzitású választ vált ki egy adott spektrum a három érzékelő-rendszerben, akkor az matematikailag a három súlyfüggvénnyel való konvolúciját jelenti a spektrummnak. Ez a három szám feleltethető meg a technikában használatos RGB koordinátáknak.

Számos probléma van itt azonban: a szem eltérően érzékeny a három tartományban érkező intenzitásra, maga az érzékelés tipikusan logaritmikus. A legnagyobb probléma, hogy a súlyfüggvények nem egészen ismertek, sőt, nem is teljesen pozitív definitek (azaz bizonyos frekvencián érkező sugárzás blokkoló hatás fejt ki egyik, vagy másik receptorokon), így a pusztán három számmal történő reprezentációban számos egyszerűsítő feltevés van, amelyek bizonyos helyzetekben problémákhoz vezethetnek.

Sztereoszkopikus megjelenítés

A fentiekben részletezett mindhárom módszer eredménye 2D-s kép. Azonban semmi nem akadályoz minket abban, hogy két képet készítsünk bármelyik eljárással ugyan arról a virtuális térről, úgy beállítva a nézeti képeket, hogy azok a két szemünk által látott képeknek felelhessenek meg. Ezek után csak az a kérdés, hogy hogyan tudjuk ezeket a képeket a szemünkre vetíteni, ezáltal teljes térhatást elérve.

A sztereoszkopikus megjelenítés azokat a technikákat foglalja magába, amelyek lehetővé teszik két különböző sík kép szemünkbe juttatását. Három nagy csoportot tudunk megkülönböztetni: a passzív szűrős, az aktív szűrős, és az auto-sztereoszkóp technikákat.

Passzív sztereoszkópia

A legrégebbi ilyen módszer az "anaglyph" eljárás, ahol két féle színnel (tipikusan piros-zöld) vetített képeket lehetett ezeknek megfelelő színszűrős szemüveggel nézni, így a szűrök mindig kiszűrték az egyik, vagy a másik képet az adott szem előtt. Ennek nyilván az a baja, hogy nem lehet színeket reprezentálni vele.

Az elvet tovább lehetett vinni úgy, hogy sűrűbben váltakoztak a spektrumban az egyik és másik szembe juttatható hullámhosszak (Infitech), ezáltal R1,R2,G1,G2,B1,B2 sávokra bontva a spektrumot, ahol az 1-es indexű sávok jutnak az egyik szembe, és a 2-es indexű sávok a másikba. Így élethű színeket kaphatunk. Az eljárás problémája, hogy az ehhez szükséges szűrők előállítása drága.

Teljesen más elven működnek a passzív sztereo megjelenítők, ahol a passzív jelző arra utal, hogy a szemüveg nem csinál semmit, abban csak két elforgatott beállítású polárszűrő található. A vetítőből egyszerre jön a kétféle polarizáltsággal a két féle kép, amely ismételten kiszűrődik a megfelelő beállítású polárszűrőn. Ennek az a hátránya, hogy normál papírral, vagy monitottal ilyen forrás nem állítható elő. Másik hátránya, hogy ha a megfigyelő elforgatja/eldönti a fejét, akkor széteshet a kép.

Az aktív sztereo megoldásnál a szemüvegek infravörös jelekkel szinkronizálva vannak a vetítőkkel. Két vetítő vetíti a két képet, a szokásos képfrissítésnél 2x magasabb frekvencián, 120 Hz-en. A szemüveg sorban kiválogatja a vetítőkből jövő képet jobb-bal-jobb-bal sorrendben.

Léteznek szemüvegmentes megvalósítások is. Ezek két nagy csoportra oszthatóak: vagy valamilyen módon követik a megfigyelő fejének/szemének mozgását, és ez alapján vetítenek két különböző képet, vagy egyszerre több különböző irányú képet vetítenek, függetlenül a szemlélő néőpontjától, de a kialakítás olyan, hogy adott pontból legerősebben csak az "odaszánt" vetület jut.

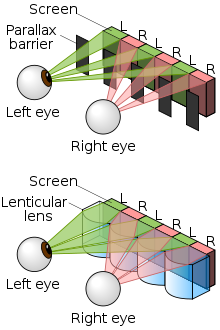
Ez utóbbak közül a parallaxis és lentikuláris módszert emeljük ki. A parallaxis módszernél az egymásba fésült jobb-bal kép előtt kis távolságra egy rács van, amely különböző szögekből nézve mindig kitkarja a nem abba szembe szánt képet vetítő pixeleket. Ez effektíve lefelezi a vízszintes felbontást, és viszonylag precíz pozíciókból nyújt csak jó minőségű térhatást. A legfejlettebb megoldások 30-40 különböző látószögből is el tudják ezt érni, de itt már nem 2 képet, hanem többet (18-at) fésülnek össze.

A lentikuláris lencséket használó rendszereknél pici lencsék sorozata van elhelyezve a képek előtt, amelyek különböző nézőirányok felé különböző képeket fókuszálnak.