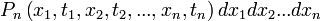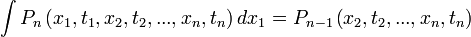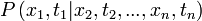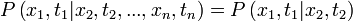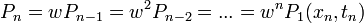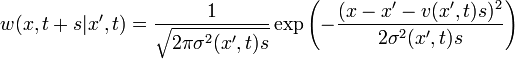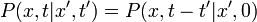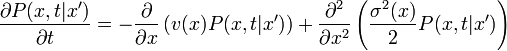Sztochasztikus folyamatok
Az alábbiakban néhány véletlenszerű folyamatot és ezek leírási módszereit tárgyaljuk.
Kauffman-hálózat
Spinüvegek
Valakinek bármi ötléete, hogy ez hogy jön ide???
Markov-lánc, Markov-folyamatok
Egy sztochasztikus folyamatot jellemezhetünk azzal, hogy diszkrét időpillanatokban a tekintett valószínűségi változó milyen értékeket vett fel. Egy rendszert akkor tekintünk leírtnak, ha meg tudjuk mondani minden időpillanatra, minden értékre a megfelelő valószínűségeket:
ahol 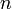 a leírni kívánt lépések száma. Mivel ez egy valószínűség, ezért minden
a leírni kívánt lépések száma. Mivel ez egy valószínűség, ezért minden 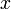 változójára kiintegrálva 1-et kell kapnunk, ez a norma-feltétel. Ezen felül, ha csak egy x változóra integrálunk, akkor az eggyel kisebb "rendű" valószínűségi kifejezést kell kapnunk:
változójára kiintegrálva 1-et kell kapnunk, ez a norma-feltétel. Ezen felül, ha csak egy x változóra integrálunk, akkor az eggyel kisebb "rendű" valószínűségi kifejezést kell kapnunk:
Tehát ha az egyik mintavételi időpontban minden lehetséges kimenetelre integrálunk, akkor olyan, mintha azt a pontot nem vennénk figyelembe. Ez a kompatibilitási feltétel.
Markov-folyamatoknál a rendszer jövőbeli állapotainak valószínűségét a korábbi, ismert állapotokból szeretnénk meghatározni. Ennek megfelelően ezt egy feltételes valószínűséggel fogalmazhatjuk meg:
azaz, ha ismert a rendszer vislkedése 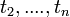 pillanatokban, akkor emellett a feltétel mellett milyen valószínűséggel lesz
pillanatokban, akkor emellett a feltétel mellett milyen valószínűséggel lesz 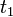 -ben
-ben 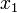 állapotban. Egy folyamat akkor Markov-folyamat, ha rendelkezik a Markov-tulajdonsággal, ami azt mondja, hogy a rendszer csak a legutóbbi állpotától függ:
állapotban. Egy folyamat akkor Markov-folyamat, ha rendelkezik a Markov-tulajdonsággal, ami azt mondja, hogy a rendszer csak a legutóbbi állpotától függ:
Ebből következik, hogyha 1 pontban ismert a Markov-folyamat, valamint az átmeneti valószínűségek, akkor teljes rendszer ismert, mert rekurzívan minden következő (vagy megelőző) állapot felírható az átmeneti valószínűségekkel:
Például ha egy diffúziós-folyamatot szeretnénk leírni, akkor az átmeneti valószínűség Gauss:
Homogénnek nevezzük a Markov-folyamatot, ha az átmeneti valószínűég időeltolás-invariáns:
Homogén diffúziós folyamatokra eben a kontextusban is levezethető a Fokker-Planck-egyenlet, ami lényegében a valószínűség-áramsűrűség megmaradását fejezi ki: