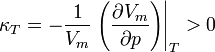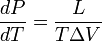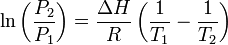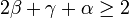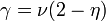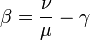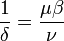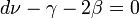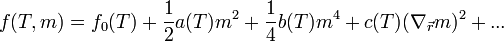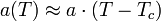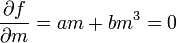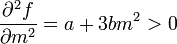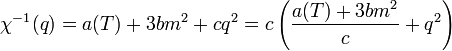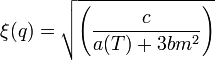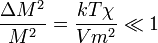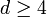Elsőrendű és folytonos fázisátalakulások
Tartalomjegyzék
Elsőrendű fázisátalakulások jellemzői
Az elsőrendű fázisátalakulásoknál tipikusan fellép valamilyen látens hő a folyamat során, amelyet a rendszer lead, vagy felvesz. Mindeközben azonban a rendszer hőmérséklete állandó. Az ilyen átmeneteket általában két fázis koegzisztenciája jellemzi: az egyik fázis még nem kezdte meg az átalakulást, miközben a másik már befejezte. Termodinamikailag az nyomás, térfogat, szabadenergia stb. folytonosak az átalakulási pontban, de deriváltjaik szakadással, vagy más szingularitással rendelkeznek.
Általános esetben, ha van egy állapotegyenletünk, akkor ott lesz fázisátalakulás, ahol az adott fázis instabillá válik. Ennek a feltétele például a folyadék-gáz átalakulásra:
ahol 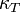 az izoterm kompresszibilitás. Általánosságban a stabilitás határát a megfelelő termodinamikai potenciál második deriváltjának a zérussá válása jelzi.
az izoterm kompresszibilitás. Általánosságban a stabilitás határát a megfelelő termodinamikai potenciál második deriváltjának a zérussá válása jelzi.
Példák
A legfontosabb példák a szilárd-folyadék, folyadék-gáz átmenetek.
Maxwell-konstrukció
 Ha a fázisdiagramm tartalmaz pozitív meredekségű részt, akkor az a fentiek miatt instabil. Legegyszerűbb példa a Van der Vaals állapotegynlet, amely a folyadék-gáz határon rendelkezik ilyen szakasszal. Ezt úgy interpretálhatjuk, hogy ebben az állapotbna a rnedszer akkor a legstabilabb, ha két fázis tart egymással egyensúlyt. Ennek megfelelően Maxwell javaslata az volt, hogy itt az állapotegyenlet görbéjét egy egyenes vonallal helyettesítsük úgy, hogy a vonal áltla elhatárolt területek egyenlőek legyenek (ugyan akkora munkát végezzen a gáz az egyik oldalon, mint amennyi a másikon felszabadulna). A két területen a rendszert túlhűtött és túlmelegített rendszernek nevezhetjük.
Ha a fázisdiagramm tartalmaz pozitív meredekségű részt, akkor az a fentiek miatt instabil. Legegyszerűbb példa a Van der Vaals állapotegynlet, amely a folyadék-gáz határon rendelkezik ilyen szakasszal. Ezt úgy interpretálhatjuk, hogy ebben az állapotbna a rnedszer akkor a legstabilabb, ha két fázis tart egymással egyensúlyt. Ennek megfelelően Maxwell javaslata az volt, hogy itt az állapotegyenlet görbéjét egy egyenes vonallal helyettesítsük úgy, hogy a vonal áltla elhatárolt területek egyenlőek legyenek (ugyan akkora munkát végezzen a gáz az egyik oldalon, mint amennyi a másikon felszabadulna). A két területen a rendszert túlhűtött és túlmelegített rendszernek nevezhetjük.
Clausius–Clapeyron-egyenlet
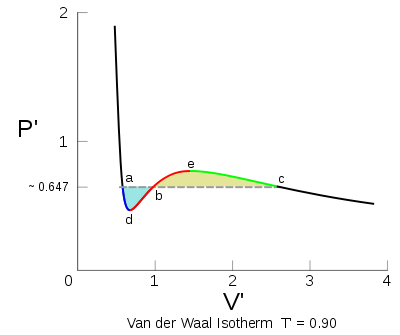
A Clausius-Clapeyron egyenlet a P-T fázisdiagrammon a koegzisztencia görbe meredekségét adja meg, elsőrendű fázisátalakulások esetén, azaz annak a göbénrek a deriváltját, amely két fázis stabil együttlétét jelöli. Az egyenlet:
ahol 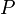 a nyomás,
a nyomás, 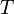 a hőmérséklet,
a hőmérséklet, 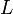 a látens hő,
a látens hő, 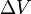 a térfogatváltozás. Speciálisan például a folyadék-gőz átmenetre az ideális gáz közelítést alkalmazva elvégezhetjük az integrálást, és egy praktikusabb alakot kaphatunk:
a térfogatváltozás. Speciálisan például a folyadék-gőz átmenetre az ideális gáz közelítést alkalmazva elvégezhetjük az integrálást, és egy praktikusabb alakot kaphatunk:
ahol 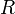 a gázállandó,
a gázállandó, 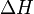 a moláris párolgáshő.
a moláris párolgáshő.
Folytonos (másodrendű) fázisátalakulások jellemzői
A folytonos fázisátalakulásokat általában a szimmetria megváltozása váltja ki: a rendszer egy rendezettebb és egy rendezetlenebb állapot között vált. A külső paraméterek függvényében a ez például valamelyik potenciál minimumainak megváltozásából eredhet (a könnyen látható esetben a negyedfokú görbe két minimuma egybe tud ovlasdni eggyé). Ezt a szuszceptiblitás divergenciája, a korrelációk végtelenné válása jelzi.
Az átmenetet a rend-paraméter jellemzi: nullától eltérő várhatóértéke jelzi az új fázis megjelenését. A rendparaméter a hőmérséklet folytonos függvénye. Például mágneses rendszerekben a mágnesezettség a rendparaméter. Ide tartozik még a konjugált-tér fogalma: ez az a tér, amivel a rendparaméter értéke eltolható. Mágneses rendszereben ez a mágneses tér.
Kritikus exponensek és skálatörvények
A megfigyelések és számolások arra a következtetésre vezettek, hogy a másodrendű fázisátalakulások a kritikus pont környékén a legkülönbözőbb mérhető mennyiségekben hatványfüggvény alakú skálázást mutatnak, amelyek alakja. Néhány ilyen kitevő:
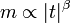 ha
ha 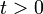 és
és 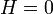
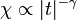 ha
ha 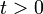 v.
v. 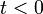 és
és 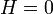
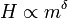 ha
ha 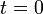 és
és 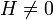
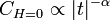 ha
ha 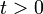 v.
v. 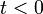 és
és 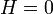
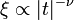 ha
ha 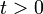 v.
v. 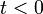 és
és 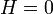
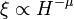 ha
ha 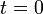 és
és 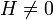
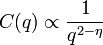 ha
ha 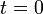 és
és 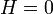
ahol 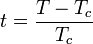 . A kritikus exponensek kiemelkedő fontosságúak a számolások és mérések, illetve különböző modellek jóslatainak összehasonlításául, mert dimenziótlan és sok más paramétertől független, könnyen számszerűsíthető, ugyanakkor jól összehasonlítható mérhető mennyiségeket jelentenek. Felmerült azonban a kérdés, hogy ezek függetlenek-e egymástól? Illetve bizonyos kísérletek arra utaltak, hogy egymástól teljesne különböző fizikai tartalmú modellekben nagyon hasonló, lényegében a mérési hiba környékén egyező kitevőket kaptak eredményül.
. A kritikus exponensek kiemelkedő fontosságúak a számolások és mérések, illetve különböző modellek jóslatainak összehasonlításául, mert dimenziótlan és sok más paramétertől független, könnyen számszerűsíthető, ugyanakkor jól összehasonlítható mérhető mennyiségeket jelentenek. Felmerült azonban a kérdés, hogy ezek függetlenek-e egymástól? Illetve bizonyos kísérletek arra utaltak, hogy egymástól teljesne különböző fizikai tartalmú modellekben nagyon hasonló, lényegében a mérési hiba környékén egyező kitevőket kaptak eredményül.
Az első összefüggésre a kritikus-exponenske között a Rushbrooke-egyenlőtlenség vetett fényt. Ez az állandó hőmésrékleten mért és az állandó nyomáson mért hőkapacitásra vonatkozó pozitivitási kritérium (ami a termodinamikai stabilitást jelenti) analógiáját vitte át mágneses rendszerekre. Ekkor az állandó mágneses tér esetében mért, és az állandó mágnesezettség esetén mért hőkapacitás kifejezéséből kapott egy egyenlőtlenséget:
- Értelmezés sikertelen (Hiányzó <code>texvc</code> végrehajtható fájl; a beállítást lásd a math/README fájlban.): C_H - C_M = T \left(\frac{\parital M}{\partial T}\right)_H^2 \left(\frac{\parital M}{\partial H}\right)_T
amibe ha beírjuk a megfelelő kitevők definícióit, akkor a következő kapcsolatot kapjuk:
Érdekes módon, minden egzaktul kiszámolható modellben ez egyenlőségként teljesül, és a kísérleti eredmények is erre utalnak! Különböző módokon több hasonló kapcoslat vezethető le a kritikus exponensek között. Így például a skála-hipotézisből (a termodinamikai mennyiségek különböző léptékeken hasonló alakjából):
Ezeken felül, még egy úgynevezett hiperskála-törvény is érvényben van, amely a fluktuációk méretére adható becslésen alapszik (l. alább), ez már függ a rendszer dimenziójától:
Ezek alapján végül csak 2 független exponens marad! A rendszerek a kritikus exponenseik alapján pedig univerzalitási osztályokba sorolhatóak: mindegy, hogy milyen fizikai folyamat, de ha 2 exponens ugyan az, akkor a két rendszer kritikus pont körüli viselkedése azonos (legfeljebb konstans faktorokban tér el). Ezen összefüggséek teljes tisztázását és értelmezését a Renormalizációs-csoportelmélet tette meg, amely alapjainak megvetése Wilson nevéhez köthető.
A Landau-elmélet
A mádosrendű-fázisátalakulásoknak egy igen szemléletes fenomenologikus elméletét adta Landau. Ez a szabadenergia szimmetria elveken elepuló sorfejtésére épít, a kritikus pont környékén, ekkor ugyanis a rendparaméter értéke kicsi, ezért ebben sorfejthetünk. A sorfejtésből a (spin)tükrözési szimmetriára hivatkozva a rendparaméterben páratlan kitevőjű tagokat eldobjuk (ezek ugyanis tükrözésre előjelet válthatnának), így a szabadenergiaűrűség kifejezése:
A kritikus pontban 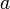 nullává válik, ezért
nullává válik, ezért 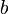 -nek pozitívnak kell lennie, hogy a szabadenergia korlátos legyen alulról, másképp fogalmazva legyen globális minimum. Hasonlóan
-nek pozitívnak kell lennie, hogy a szabadenergia korlátos legyen alulról, másképp fogalmazva legyen globális minimum. Hasonlóan  -nek is pozitívnak kell lennie ahhoz, hogy a homogén állapot legyen a legstabilabb. A kritikus pont környéki viselkedés leírásához elég ennyi tagot megtartani, magasabb rendű tagok csak akkor szükségesek, ha a negyedrendű tag is zérussá válik, ekkor a következő megtartható tag szükséges a minimum biztosításához.
-nek is pozitívnak kell lennie ahhoz, hogy a homogén állapot legyen a legstabilabb. A kritikus pont környéki viselkedés leírásához elég ennyi tagot megtartani, magasabb rendű tagok csak akkor szükségesek, ha a negyedrendű tag is zérussá válik, ekkor a következő megtartható tag szükséges a minimum biztosításához.
Mivel 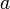 előjelet vált a kritikus pontban, ezért a viselkedését lineárissal közelíthetjük:
előjelet vált a kritikus pontban, ezért a viselkedését lineárissal közelíthetjük:
a többi együttható-függvényt pedig konstanssal közelítjük. Egytengelyű Ising ferromágnesre a mágnesezettség skalár, ekkor a szabadenergia minimumát egyszerűen a derivált zérusááv álásának egyenletéből kapjuk:
miközben a második derivált pozitív:
maga a második derivált definíció szerint a szuszceptibilitás reciproka, 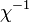 . Az egyéb jellemző mennyiségek származtatása már csak deriválgatás, például az entrópia-sűrűség:
. Az egyéb jellemző mennyiségek származtatása már csak deriválgatás, például az entrópia-sűrűség: 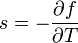 vagy a hőkapacitás:
vagy a hőkapacitás:  stb.
stb.
A korrelációs-hossz, mint fázisátalakulást jelző másik fontos mennyiség a mágenesezettség (vagy spinsűrűség) kis fluktuációból vezethető le. A szuszceptibilitás Fourier-transzformáltja ekkor:
Ebből azonban definíció szerint a  melletti másik tag a korrelációs hossz reiprokának négyzete, így:
melletti másik tag a korrelációs hossz reiprokának négyzete, így:
innen látszik, hogy a kritikus hőmérséklet környékén (ahol 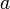 -t lineárisan közelítjük) a korrelációs hossz
-t lineárisan közelítjük) a korrelációs hossz 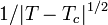 -el divergál.
-el divergál.
A Landau-elméletnek azonban vannak problémái is. Nevezetesen nem veszi figyelembe a fluktuációkat (mindenhol, ahol 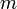 -et használunk ott a mágnesezettségre kihasználtuk, hogy éles eloszlással rendelkezik, ezért a várható értékét a legvalószínűbb értékével helyettesítettük!). Az elmélet korlátját a Ginzburg-kritérium adja, amely számszerűsíti, hogy mikor jogos a fluktuációk elhanyagolása:
-et használunk ott a mágnesezettségre kihasználtuk, hogy éles eloszlással rendelkezik, ezért a várható értékét a legvalószínűbb értékével helyettesítettük!). Az elmélet korlátját a Ginzburg-kritérium adja, amely számszerűsíti, hogy mikor jogos a fluktuációk elhanyagolása:
ahol 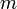 a mágnesezettség-sűrűség,
a mágnesezettség-sűrűség,  a teljes mágnesezettség,
a teljes mágnesezettség, 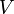 a térfogat. Termodinamikai határesetben az kell, hogy a rendszer mérete minden irányban legalább a korrelációs-hossz legyen, ezért
a térfogat. Termodinamikai határesetben az kell, hogy a rendszer mérete minden irányban legalább a korrelációs-hossz legyen, ezért 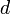 dimenziós rendszerre
dimenziós rendszerre 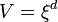 -t írhatunk, ekkor annak a feltétele, hogy a fluktuációk ne nőhessenek végtelen nagyra a kritikus pont környékén az, hogy a fenti érték skálázási kitevője 1 legyen. Beírva, hogy a mágnesezettség négyzetének kitevője -1 (a fenti 1. derivált=0 kifejezésből),
-t írhatunk, ekkor annak a feltétele, hogy a fluktuációk ne nőhessenek végtelen nagyra a kritikus pont környékén az, hogy a fenti érték skálázási kitevője 1 legyen. Beírva, hogy a mágnesezettség négyzetének kitevője -1 (a fenti 1. derivált=0 kifejezésből), 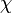 kitevője 1,
kitevője 1, 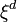 pedig
pedig 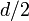 -vel skálázik, azt a feltételt kapjuk, hogy:
-vel skálázik, azt a feltételt kapjuk, hogy:
azaz 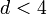 -re a fluktuációk végtelen nagyra nőnek a rendszerben! Ez az egész azonban csak rövid távú kölcsönhatásokra igaz hosszú távú kölcsönhatások esetén a kritikus dimenzió lejjebb is csúszhat. 3D-ben azonban az is probléma, hogy a kritikus pont körüli aszimptotikus viselkedést is rosszul adja meg az elmélet. Mindezek ellenére létezik olyan tartomány, ahol a Landau-leírás már jó a fenti értelemben és a sorfejtés pontossága is elégséges, nevezetesen a szupravezető átalakulások leírása. Ezen a téren az elmélet jelentős sikereket ért el.
-re a fluktuációk végtelen nagyra nőnek a rendszerben! Ez az egész azonban csak rövid távú kölcsönhatásokra igaz hosszú távú kölcsönhatások esetén a kritikus dimenzió lejjebb is csúszhat. 3D-ben azonban az is probléma, hogy a kritikus pont körüli aszimptotikus viselkedést is rosszul adja meg az elmélet. Mindezek ellenére létezik olyan tartomány, ahol a Landau-leírás már jó a fenti értelemben és a sorfejtés pontossága is elégséges, nevezetesen a szupravezető átalakulások leírása. Ezen a téren az elmélet jelentős sikereket ért el.