A statisztikus fizikai szimulációk alapjai és a Monte Carlo módszer

Innen: TételWiki
A lap korábbi változatát látod, amilyen Adrian (vitalap | szerkesztései) 2011. június 9., 19:17-kor történt szerkesztése után volt.

Statisztikus fizikai szimulációk alapjai

Molekuladinamika

A Metropolis algoritmus

A Metropolis algoritmussal a statisztikus fizikai rendszer energiaminimumát találhatjuk meg, ahogy azt a szimulált hőkezelés témakörében is láttuk. Az algoritmus a következő:

  1. Induljunk ki egy A konfigurációból, aminek tudjuk az EA energiáját.
  2. Változtassunk a rendszeren, hogy egy A-hoz közeli B konfigurációt kapjunk. Számoljuk ki a konfiguráció EB energiáját.
  3. Ha EB < EA, fogadjuk el ezt az új konfigurációt (így a Boltzmann-faktornak is eleget teszünk).
  4. Ha EB > EA, az új állapotot 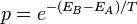p = e^{-(E_B-E_A)/T} valószínűséggel elfogadjuk.

A hőmérséklet folyamatos csökkentésével az algoritmus bekonvergál az energiaminimumba.

A Monte-Carlo módszer

MSc záróvizsga tételek
Tételek Soktest rendszerek | Transzportfolyamatok | Véletlen gráfok generálása, tulajdonságai | Elsőrendű és folytonos fázisátalakulások | Válasz- és korrelációs függvények, fluktuáció-disszipáció tétel | Sztochasztikus folyamatok | A statisztikus fizikai szimulációk alapjai és a Monte Carlo módszer | Dinamikai rendszerek, kaotikus viselkedés | Adatelemzés: lineáris és nem lineáris regresszió egy modellen bemutatva | Adatelemzés: bootstrap modellek | TCP hálózat működése | Adatelemzés: ARCH, GARCH folyamatok | Numerikus módszerek | Vizualizációs módszerek
A lap eredeti címe: „http://tetelwiki.mafihe.hu/index.php?title=A_statisztikus_fizikai_szimulációk_alapjai_és_a_Monte_Carlo_módszer&oldid=615”