A statisztikus fizikai szimulációk alapjai és a Monte Carlo módszer
A lap korábbi változatát látod, amilyen Adrian (vitalap | szerkesztései) 2011. június 9., 20:55-kor történt szerkesztése után volt.
Tartalomjegyzék
Statisztikus fizikai szimulációk alapjai
Molekuladinamika
A Metropolis algoritmus
A Metropolis algoritmussal a statisztikus fizikai rendszer energiaminimumát találhatjuk meg, ahogy azt a szimulált hőkezelés témakörében is láttuk. Az algoritmus a következő:
- Induljunk ki egy A konfigurációból, aminek tudjuk az EA energiáját.
- Változtassunk a rendszeren, hogy egy A-hoz közeli B konfigurációt kapjunk. Számoljuk ki a konfiguráció EB energiáját.
- Ha EB < EA, fogadjuk el ezt az új konfigurációt (így a Boltzmann-faktornak is eleget teszünk).
- Ha EB > EA, az új állapotot
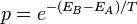 valószínűséggel elfogadjuk.
valószínűséggel elfogadjuk.
A hőmérséklet folyamatos csökkentésével az algoritmus bekonvergál az energiaminimumba.
A Monte-Carlo módszer
A Monte-Carlo módszernek nevezzük az olyan eljárásokat, amelyek a problémákat random számok és valószínűségek felhasználásával oldják meg. Az eljárás során ismétlődően kiértékelünk egy determinisztikus modellt, random számokat használva inputnak. Akkor használják, ha a feladat nagyon összetett, nemlineáris, vagy nagyon sok paramétertől függ.
Használata:
- Állítsuk föl a modellt: y = f(x1, x2, ..., xq)
- Generáljunk random számokat inputnak: xi1, xi2, ..., xiq
- Értékeljük ki a modellt, az eredményt tároljuk el yi-ben
- Ismételjük a 2. és 3. lépéseket n-szer
- Elemezzük az eredményeket hisztogram, összesítő statisztikák, stb. segítségével