A statisztikus fizikai szimulációk alapjai és a Monte Carlo módszer

Molekuladinamika

A molekuladinamika a részecskék mikroszkopikus dinamikájának követésével foglalkozik. Valódi rendszerben 10²³ nagyságrendű részecske van, ezt a mai számítógépekkel szimulálni lehetetlen. Azonban ennél kevesebb részecskét is elég szimulálnunk ahhoz, hogy a termodinamikai tulajdonságokat vizsgálhassuk. A szimulációkban a párkölcsönhatásokat vesszük figyelembe, ám lehetséges közelítéseket tenni. A részecskék közt a Van der Waals erő hat, ami elég gyorsan lecseng, így távoli részecskék közt elhanyagolható (ezen a pontot különbözik a molekuladinamika és a gravitációs N-test szimuláció, ahol az 1/r²-es erő miatt nem hanyagolható el a kölcsönhatás).

A szimulációban van tehát N darab részecske, melyekre a Newton-törvények alapján kiszámítjuk a rájuk ható erőt, majd léptetjük a rendszert. Mivel a kezdőállapotokat általában nem a termodinamikai egyensúlyból indítjuk, meg kell várni, hogy a rendszer beálljon abba. Hogy mikor állt be, azt az ekvipartíció segítségével mutathatjuk ki:

$\left \langle \frac{1}{2}mv^2 \right \rangle = \frac{3}{2}kT$

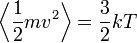
Ha a rendszer elérte az egyensúlyi állapotát, mérhetővé válnak a termodinamikai változók (hőmérséklet, nyomás, hőkapacitás, stb.)

Verlet-algoritmus

Molekuladinamikai szimulációkban legtöbbször a Verlet-algoritmust használják a diffegyenletek megoldására. A Runge-Kuttával szemben több előnye van:

• gyorsabb, mert egy lépésben csak egyszer kell a gyorsulásokat számolni
• majdnem olyan pontos, mint a RK4 ($O(\tau^4) \text{vs.} O(\tau^5)$)
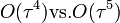• jól megőrzi az energiát
• időtükrözésre nem változik (ez a részleges egyensúly feltétele miatt fontos)

A Verlet-algoritmus egy lépése (R(t) a koordináták, V(t) a sebességek, A(t) a gyorsulások):

$R_{n+1} = 2R_n - R_{n-1} + \tau^2 A_n + O(\tau^4)\,$

$V_n = \frac{R_{n+1} - R_{n-1}}{2\tau} + O(\tau^2)$

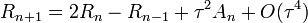
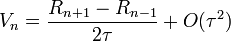
Hátrányai:

• két előző lépést használ, így nem indítható 1 kezdeti feltételből
• a sebesség és a pozíció nem egyszerre frissítődik, a sebesség "le van maradva"

Megoldás: velocity-Verlet algoritmus:

• R-ben már csak 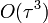$O(\tau^3)$ pontosságú
• ez már nem 2 előző lépést használ
• koordináták és sebességek egyszerre frissülnek
• sebesség is 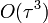$O(\tau^3)$ pontosságú

A Metropolis algoritmus

A Metropolis algoritmussal a statisztikus fizikai rendszer energiaminimumát találhatjuk meg, ahogy azt a szimulált hőkezelés témakörében is láttuk. Az algoritmus a következő:

1. Induljunk ki egy A konfigurációból, aminek tudjuk az E_A energiáját.
2. Változtassunk a rendszeren, hogy egy A-hoz közeli B konfigurációt kapjunk. Számoljuk ki a konfiguráció E_B energiáját.
3. Ha E_B < E_A, fogadjuk el ezt az új konfigurációt (így a Boltzmann-faktornak is eleget teszünk).
4. Ha E_B > E_A, az új állapotot 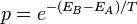$p = e^{-(E_B-E_A)/T}$ valószínűséggel elfogadjuk.

A hőmérséklet folyamatos csökkentésével az algoritmus bekonvergál az energiaminimumba.

A Monte-Carlo módszer

A Monte-Carlo módszernek nevezzük az olyan eljárásokat, amelyek a problémákat random számok és valószínűségek felhasználásával oldják meg. Az eljárás során ismétlődően kiértékelünk egy determinisztikus modellt, random számokat használva inputnak. Akkor használják, ha a feladat nagyon összetett, nemlineáris, vagy nagyon sok paramétertől függ.

Használata:

1. Állítsuk föl a modellt: y = f(x₁, x₂, ..., x_q)
2. Generáljunk random számokat inputnak: x_i1, x_i2, ..., x_iq
3. Értékeljük ki a modellt, az eredményt tároljuk el y_i-ben
4. Ismételjük a 2. és 3. lépéseket n-szer
5. Elemezzük az eredményeket hisztogram, összesítő statisztikák, stb. segítségével