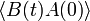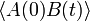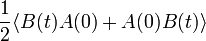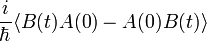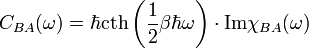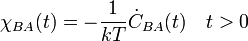Válasz- és korrelációs függvények, fluktuáció-disszipáció tétel
Ebbe a tételbe sok minden a Sasi-féle Nemegyensúlyi Statisztikus Fizika órából fog bekerülni.
Tartalomjegyzék
Lineáris válasz-elmélet
Kis külső perturbáció hatására a legkülönbözőbb fizikai rendszerek által produkált reakciók is jól tárgyalhatók lineáris közelítésben. Ide értendőek nem csak a korábban tárgyalt transzport jelenségek, de maguk a mérések is: például mechanikai vagy termodinamikai változásnak teszünk ki egy rendszert egy 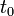 időpontban és megmérjük a különböző jellemzőit egy
időpontban és megmérjük a különböző jellemzőit egy 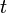 időpontban. A rendszert leíró fizikai jellemzők itt is első rendben lineáris kapcsolatba hozhatóak a perturbációval.
időpontban. A rendszert leíró fizikai jellemzők itt is első rendben lineáris kapcsolatba hozhatóak a perturbációval.
A tárgyaláshoz legyen az izolált (nem-perturbált) rendszer Hamiltonja 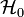 és a kölcsönhatást leíró Hamilton
és a kölcsönhatást leíró Hamilton 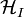 , valamint a teljes rendszert jellemző Hamilton ezek összege. Tételezzük fel a külső perturbációról nem csak azt, hogy gyenge, de azt is, hogy adiabatikusan kapcsoljuk be, azaz nagyon lassan, kvázi-stacionárius állapotokon keresztül.
, valamint a teljes rendszert jellemző Hamilton ezek összege. Tételezzük fel a külső perturbációról nem csak azt, hogy gyenge, de azt is, hogy adiabatikusan kapcsoljuk be, azaz nagyon lassan, kvázi-stacionárius állapotokon keresztül.
A rendszert jellemezzük a sűrűségoperátorral, 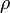 -val. Egy
-val. Egy 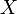 mennyiség sokaságátlaga
mennyiség sokaságátlaga 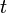 időpontban:
időpontban:
ahol 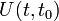 az időfejlesztés unitér operátora, amely leírja a rendszert jellemző mennyiségek időfejlődését
az időfejlesztés unitér operátora, amely leírja a rendszert jellemző mennyiségek időfejlődését 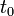 -ból
-ból 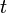 -be. A kölcsönhatási képben minden operátor (így
-be. A kölcsönhatási képben minden operátor (így 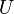 is) a szabad Hamilton szerint fejlődik időben:
is) a szabad Hamilton szerint fejlődik időben:
Ennek a megoldása 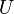 -ra egy exponenciális kifejezést ad, amit első rendig sorfejtve kapjuk, hogy:
-ra egy exponenciális kifejezést ad, amit első rendig sorfejtve kapjuk, hogy:
Ezt beírva az X mennyiség átlagának képletébe, és kihasználva a Tr ciklikusságát, valamint, hogy kezdetben a rendszer termikus egyensúlyban volt: 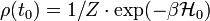 , továbbá a külső perturbációja legyen
, továbbá a külső perturbációja legyen 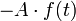 alakú, ahol
alakú, ahol 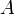 a perturbáló mennyiség operátora,
a perturbáló mennyiség operátora, 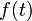 pedig a perturbáció amplitudója. Mindezekkel kapjuk:
pedig a perturbáció amplitudója. Mindezekkel kapjuk:
Mivel a Tr alatti ciklikus permutációs szimmetria van érvényben, az időfüggések átcsoportosíthatóak, ezért a []-es mennyiség csak az időkülönbéstől függ. Ezekkel kapjuk a Kubo-formulát:
ahol:
a szuszceptibilitás, vagy lineáris válasz függvény.
Korrelációs függvények
Két mennyiség korrelációs függvényét igen sokféle alakban fel lehet írni. Például:
Belátható, hogy ezek közül csak 1 függtelen van.
Fluktuáció-disszipáció tétel
A korrelációs-függvény és a lineáris válaszfüggvény között a Fourier-térben egyszerű alakú kapcsolat áll fent:
A korrelációs függvény az egyensúlyi fluktuációkat jellemzi, míg a lineáris válaszfüggvény képzetes része a rendszer irreverzibilis megváltozását (pl. disszipáció) jellemzi, amiközben törekszik az egyensúly felé.
Klasszikus határesetben azt kapjuk, hogy:
ahol a klasszikusság feltétele, hogy a rendszer átmenetei sokkal kisebb energiájúak legyenek, mint a hőmérsékleti fluktuációk jellemző energiái: 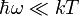
Ez a kapcsolat azést is fontos, mert a korrelációs-függvények aránylag könnyen mérhetők (pl: neutron-szórás kísérletek a nukleon-nukleon sűrűség korrelációs függvénnyel arányosak) ezáltal pedig megkaphatjuk a válaszfüggvény képzetes részét is. Magát a válszfüggvényt teljes egészében előállíthatjuk csupán a képzetes rész ismeretéből.
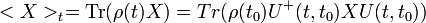
![i\hbar \frac{dU}{dt} = [U, \mathcal{H}_0]](/images/math/6/5/6/6560535c87f8094cac44301c2d173f61.png)
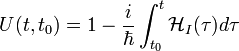
![<X>_t = <X>_0 + \frac{i}{\hbar}\int_{-\infty}^t d\tau \mathrm{Tr}\left[ \frac{\exp(-\beta\mathcal{H}_0)}{Z} (X(t)A(\tau)-A(\tau)X(t)) \right]f(\tau)](/images/math/8/2/5/825e1fd50b75ed51318b44846c9fb30c.png)
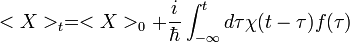
![\chi(t) = \mathrm{Tr}\left[ \frac{\exp(-\beta\mathcal{H}_0)}{Z} (X(t)A(0)-A(0)X(t)) \right]](/images/math/7/0/7/70748a697684b5dc9a03715affde58dd.png)