Adatelemzés: lineáris és nem lineáris regresszió egy modellen bemutatva

Általános statisztikai jellemzők

(Átlag szórás, kovariancia...)

Modellek illesztése

Lineáris regresszió

A most leírt modell tulajdonságai a következők:

• prediktor változó: x
• az y-ok függetlenek
• adott x-re kapott y-ok normál eloszlásúak olyan átlaggal, ami az x lineáris függvényeként kapható meg

• Feladat: adott x-re y-t megmondani. A straight line regression model (egyenes vonal illesztő modell) alakja a köv:

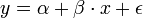$y = \alpha + \beta \cdot x + \epsilon$, vagy indexesen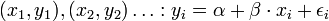 $(x_1, y_1), (x_2, y_2) \ldots: y_i = \alpha + \beta \cdot x_i + \epsilon_i$

A normál analízis során azt feltételezzük, hogy epsilon_i-k független és azonosan 0 átlagú és szigma^2 szórású normál eloszlást követő változók. Az alfa+beta*x a determinisztikus rész, az epsilon_i a random zaj. Az előbbi érdekel minket.

Az illesztés során a legkisebb négyzetek módszerét használhatjuk.

Legkisebb négyzetek módszere

Tegyük fel, hogy 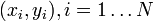$(x_i, y_i), i = 1 \ldots N$ mérési adatokra akarunk függvényt illeszteni, melynek paraméterei 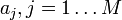$a_j, j = 1 \ldots M$, azaz

$y(x) = x(x;a_1,a_2,\ldots,a_m)$

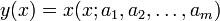
A legkisebb négyzetek módszere a következő módon keresi a paramétereket:

Értelmezés sikertelen (Hiányzó <code>texvc</code> végrehajtható fájl; a beállítást lásd a math/README fájlban.): {min}_{a_1 \ldots a_m}\left( \sum_{i=1}^N [y_i - y(x_i;a_1,\ldots,\a_m)]^2 \right)

Ez azért jó, mert megadja a paraméterek legvalószínűbb halmazát. Természetesen lehetne más költségfüggvényt is használni.