Adatelemzés: lineáris és nem lineáris regresszió egy modellen bemutatva
Tartalomjegyzék
Általános statisztikai jellemzők
(Átlag szórás, kovariancia...)
Modellek illesztése
Lineáris regresszió
A most leírt modell tulajdonságai a következők:
- prediktor változó: x
- az y-ok függetlenek
- adott x-re kapott y-ok normál eloszlásúak olyan átlaggal, ami az x lineáris függvényeként kapható meg
- Feladat: adott x-re y-t megmondani. A straight line regression model (egyenes vonal illesztő modell) alakja a köv:
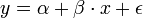 , vagy indexesen
, vagy indexesen 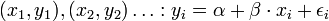
A normál analízis során azt feltételezzük, hogy epsilon_i-k független és azonosan 0 átlagú és szigma^2 szórású normál eloszlást követő változók. Az alfa+beta*x a determinisztikus rész, az epsilon_i a random zaj. Az előbbi érdekel minket.
Az illesztés során a legkisebb négyzetek módszerét használhatjuk.
Legkisebb négyzetek módszere
Tegyük fel, hogy 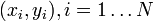 mérési adatokra akarunk függvényt illeszteni, melynek paraméterei
mérési adatokra akarunk függvényt illeszteni, melynek paraméterei 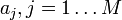 , azaz
, azaz
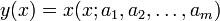
A legkisebb négyzetek módszere a következő módon keresi a paramétereket:
![{min}_{a_1 \ldots a_m}\left( \sum_{i=1}^N [y_i - y(x_i;a_1,\ldots,a_m)]^2 \right)](/images/math/f/8/e/f8eb22779db531d78f6c8209a59c331e.png)
Ez azért jó, mert megadja a paraméterek legvalószínűbb halmazát. Természetesen lehetne más költségfüggvényt is használni, de ez a modell arra a kérdésre ad választ, hogy mely paramétervektor esetén a maximális a valószínűsége annak, hogy az adott mérési eredményeket kapjuk. Ez a maximális valószínűségű paraméterbecslés.
Ha csak az 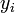 adatok mérési hibáját vesszük figyelembe és az a hiba Gauss eloszlású, valamint a hiba eloszlásának szórása azonos mindegyik mérési pontban (ha ezek nem teljesülnek, akkor a módszer nem a legnagyobb valószínűséghez tartozó paramétereket adja), akkor a fenti valószínűség átírható így:
adatok mérési hibáját vesszük figyelembe és az a hiba Gauss eloszlású, valamint a hiba eloszlásának szórása azonos mindegyik mérési pontban (ha ezek nem teljesülnek, akkor a módszer nem a legnagyobb valószínűséghez tartozó paramétereket adja), akkor a fenti valószínűség átírható így:
![P \propto \prod_{i=1}^N \left\{ exp \left[ -\frac{1}{2} \left( \frac{y_i - y(x_i)}{\sigma} \right)^2 \right] \Delta y \right\}](/images/math/f/5/1/f516dc767b84b61799210b8055386244.png)
Ennek keressük a maximumát (vagy ha vesszük a negatív logaritmuást, akkor a minimumát):
![-log(P) = \left[ \sum_{i=1}^N \frac{[y_i - y(x_i)]^2}{\sigma} \right] - N log(\Delta y)](/images/math/2/6/a/26a7091326e38e29313e516a3cf8ccc6.png)
Mivel N, 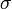 és
és 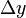 állandók, ez pont a legkisebb négyzetek módszerét adja és P értéke megmondja, hogy mennyire jó az illesztés.
állandók, ez pont a legkisebb négyzetek módszerét adja és P értéke megmondja, hogy mennyire jó az illesztés.
A Khí-négyzet módszer
Ha a mérési pontok hibájának szórása nem egyforma (de továbbra is normál eloszlást követnek), akkor a legkisebb négyzetek módszerét könnyen általánosíthatjuk. Ez a Khí-négyzet illesztés, amelynek költségfüggvénye a következő:
Értelmezés sikertelen (Hiányzó <code>texvc</code> végrehajtható fájl; a beállítást lásd a math/README fájlban.): \khi^2 = \sum_{i=1}^N \left( \frac{y_i - y(x_i;a_1, \ldots a_M}{\sigma_i} \right)^2
Tekinthetjük úgy, hogy a 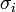 szórásokkal súlyozzuk az eltéréseket, vagy másképpen egységnyi szórásúra normálunk minden pontnál.
szórásokkal súlyozzuk az eltéréseket, vagy másképpen egységnyi szórásúra normálunk minden pontnál.
Mivel a mérési pontokról feltételeztük, hogy normál eloszlást követnek, Értelmezés sikertelen (Hiányzó <code>texvc</code> végrehajtható fájl; a beállítást lásd a math/README fájlban.): \khi^2
ilyen véletlen változók négyzetének összege. Az ilyen típusú valószínűségi változók nem Gauss eloszlást, hanem az úgynevezett (N - M) szabadsági fokú Khí-négyzet eloszlást követik. Ha az 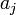 paraméterek lineárisan szerepelnek akkor ez az eloszlás analitikusan megadható, így megmondható annak valószínűsége (Q), hgoy az adott paraméterekkel jellemzett modellen végzett mérés Értelmezés sikertelen (Hiányzó <code>texvc</code> végrehajtható fájl; a beállítást lásd a math/README fájlban.): \khi^2
-nél nagyobb eltérést ad. Értelmezés sikertelen (Hiányzó <code>texvc</code> végrehajtható fájl; a beállítást lásd a math/README fájlban.): \left( Q \approx 0,1
tipikus,
paraméterek lineárisan szerepelnek akkor ez az eloszlás analitikusan megadható, így megmondható annak valószínűsége (Q), hgoy az adott paraméterekkel jellemzett modellen végzett mérés Értelmezés sikertelen (Hiányzó <code>texvc</code> végrehajtható fájl; a beállítást lásd a math/README fájlban.): \khi^2
-nél nagyobb eltérést ad. Értelmezés sikertelen (Hiányzó <code>texvc</code> végrehajtható fájl; a beállítást lásd a math/README fájlban.): \left( Q \approx 0,1
tipikus, 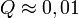 elfogadható,
elfogadható, 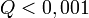 rossz modellre vagy hibabecslésre utal Értelmezés sikertelen (Hiányzó <code>texvc</code> végrehajtható fájl; a beállítást lásd a math/README fájlban.): \right)
. Fontos, hogy a mérési hibák becslése jó legyen, különben megtévesztő eredményre juthatunk.
rossz modellre vagy hibabecslésre utal Értelmezés sikertelen (Hiányzó <code>texvc</code> végrehajtható fájl; a beállítást lásd a math/README fájlban.): \right)
. Fontos, hogy a mérési hibák becslése jó legyen, különben megtévesztő eredményre juthatunk.
Annak feltétele, hogy a Értelmezés sikertelen (Hiányzó <code>texvc</code> végrehajtható fájl; a beállítást lásd a math/README fájlban.): \khi^2
-nek minimuma van az, hogy az 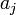 paraméterek szerinti deriváltja 0 legyen.
paraméterek szerinti deriváltja 0 legyen.