Adatelemzés: lineáris és nem lineáris regresszió egy modellen bemutatva
Tartalomjegyzék
Általános statisztikai jellemzők
Alapfogalmak:
- Átlag: ha van N darab adatpontunk (egy X vektorba rendezve), mindegyiket
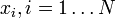 -vel jelöljük, akkor az átlag:
-vel jelöljük, akkor az átlag: ![E[X] = \mu = \bar{x} = \frac{1}{N} \sum_{i=1}^N x_i](/images/math/7/a/0/7a0451a68312c8535090611e6e6cb5b5.png)
- Szórás: ha van N db,
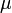 átlagú adatpontunk, akkor ezek szórása:
átlagú adatpontunk, akkor ezek szórása: ![\sigma = \sqrt{E\left[ X - \mu \right]^2}](/images/math/a/8/1/a818f8e2bcfa670e582930973ba6a62e.png)
- Kovariancia: a kovariancia megadja két egymástól különböző változó (X,Y) együttmozgását:
![Cov(X,Y) = E \left[ \left( X - E[X] \right) \left( Y - E[Y] \right) \right] = E[XY] - E[X]\cdot E[Y]](/images/math/6/8/6/6865c57a571ede23340db46bd38b24bc.png)
- Kovariancia mátrix: egy n adatpontból álló X és egy m adatpontból álló Y vektor kovariancia mátrixa:
- Keresztkorreláció:
- Autokorreláció:
(Átlag szórás, kovariancia...)
Modellek illesztése
Lineáris regresszió
A most leírt modell tulajdonságai a következők:
- prediktor változó: x
- az y-ok függetlenek
- adott x-re kapott y-ok normál eloszlásúak olyan átlaggal, ami az x lineáris függvényeként kapható meg
- Feladat: adott x-re y-t megmondani. A straight line regression model (egyenes vonal illesztő modell) alakja a köv:
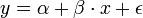 , vagy indexesen
, vagy indexesen 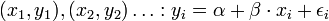
A normál analízis során azt feltételezzük, hogy epsilon_i-k független és azonosan 0 átlagú és szigma^2 szórású normál eloszlást követő változók. Az alfa+beta*x a determinisztikus rész, az epsilon_i a random zaj. Az előbbi érdekel minket.
Az illesztés során a legkisebb négyzetek módszerét használhatjuk.
Legkisebb négyzetek módszere
Tegyük fel, hogy 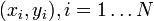 mérési adatokra akarunk függvényt illeszteni, melynek paraméterei
mérési adatokra akarunk függvényt illeszteni, melynek paraméterei 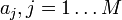 , azaz
, azaz
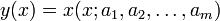
A legkisebb négyzetek módszere a következő módon keresi a paramétereket:
![{min}_{a_1 \ldots a_m}\left( \sum_{i=1}^N [y_i - y(x_i;a_1,\ldots,a_m)]^2 \right)](/images/math/f/8/e/f8eb22779db531d78f6c8209a59c331e.png)
Ez azért jó, mert megadja a paraméterek legvalószínűbb halmazát. Természetesen lehetne más költségfüggvényt is használni, de ez a modell arra a kérdésre ad választ, hogy mely paramétervektor esetén a maximális a valószínűsége annak, hogy az adott mérési eredményeket kapjuk. Ez a maximális valószínűségű paraméterbecslés.
Ha csak az 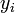 adatok mérési hibáját vesszük figyelembe és az a hiba Gauss eloszlású, valamint a hiba eloszlásának szórása azonos mindegyik mérési pontban (ha ezek nem teljesülnek, akkor a módszer nem a legnagyobb valószínűséghez tartozó paramétereket adja), akkor a fenti valószínűség átírható így:
adatok mérési hibáját vesszük figyelembe és az a hiba Gauss eloszlású, valamint a hiba eloszlásának szórása azonos mindegyik mérési pontban (ha ezek nem teljesülnek, akkor a módszer nem a legnagyobb valószínűséghez tartozó paramétereket adja), akkor a fenti valószínűség átírható így:
![P \propto \prod_{i=1}^N \left\{ exp \left[ -\frac{1}{2} \left( \frac{y_i - y(x_i)}{\sigma} \right)^2 \right] \Delta y \right\}](/images/math/f/5/1/f516dc767b84b61799210b8055386244.png)
Ennek keressük a maximumát (vagy ha vesszük a negatív logaritmuást, akkor a minimumát):
![-log(P) = \left[ \sum_{i=1}^N \frac{[y_i - y(x_i)]^2}{\sigma} \right] - N log(\Delta y)](/images/math/2/6/a/26a7091326e38e29313e516a3cf8ccc6.png)
Mivel N, 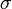 és
és 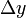 állandók, ez pont a legkisebb négyzetek módszerét adja és P értéke megmondja, hogy mennyire jó az illesztés.
állandók, ez pont a legkisebb négyzetek módszerét adja és P értéke megmondja, hogy mennyire jó az illesztés.
A Khí-négyzet módszer
Ha a mérési pontok hibájának szórása nem egyforma (de továbbra is normál eloszlást követnek), akkor a legkisebb négyzetek módszerét könnyen általánosíthatjuk. Ez a Khí-négyzet illesztés, amelynek költségfüggvénye a következő:
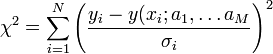
Tekinthetjük úgy, hogy a 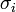 szórásokkal súlyozzuk az eltéréseket, vagy másképpen egységnyi szórásúra normálunk minden pontnál.
szórásokkal súlyozzuk az eltéréseket, vagy másképpen egységnyi szórásúra normálunk minden pontnál.
Mivel a mérési pontokról feltételeztük, hogy normál eloszlást követnek, 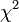 ilyen véletlen változók négyzetének összege. Az ilyen típusú valószínűségi változók nem Gauss eloszlást, hanem az úgynevezett (N - M) szabadsági fokú Khí-négyzet eloszlást követik. Ha az
ilyen véletlen változók négyzetének összege. Az ilyen típusú valószínűségi változók nem Gauss eloszlást, hanem az úgynevezett (N - M) szabadsági fokú Khí-négyzet eloszlást követik. Ha az 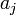 paraméterek lineárisan szerepelnek akkor ez az eloszlás analitikusan megadható, így megmondható annak valószínűsége (Q), hgoy az adott paraméterekkel jellemzett modellen végzett mérés
paraméterek lineárisan szerepelnek akkor ez az eloszlás analitikusan megadható, így megmondható annak valószínűsége (Q), hgoy az adott paraméterekkel jellemzett modellen végzett mérés 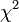 -nél nagyobb eltérést ad. (
-nél nagyobb eltérést ad. (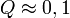 tipikus,
tipikus, 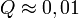 elfogadható,
elfogadható, 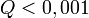 rossz modellre vagy hibabecslésre utal). Fontos, hogy a mérési hibák becslése jó legyen, különben megtévesztő eredményre juthatunk.
rossz modellre vagy hibabecslésre utal). Fontos, hogy a mérési hibák becslése jó legyen, különben megtévesztő eredményre juthatunk.
Annak feltétele, hogy a 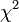 -nek minimuma van az, hogy az
-nek minimuma van az, hogy az 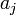 paraméterek szerinti deriváltja 0 legyen.
paraméterek szerinti deriváltja 0 legyen.
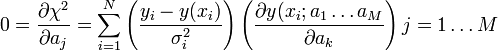
Ez általában M nemlináris egyenletből álló rendszerre vezet, de ha az 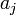 paraméterek lineárisan szerepelnek az y(x; a_1 \ldots a_M) kifejezésben, akkor az egyenletek is lineárisak lesznek.
paraméterek lineárisan szerepelnek az y(x; a_1 \ldots a_M) kifejezésben, akkor az egyenletek is lineárisak lesznek.
Példa: egyenes illesztés
Legegyszerűbb példa a lineáris regresszióra az egyenesillesztés.
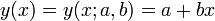
A költségfüggvényünk most:
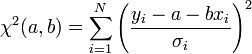
A minimumban a deriváltak eltűnnek:
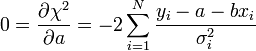
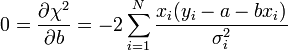
A fenti kifejezésekben a szummákat szétbonthatjuk az alábbi jelölések segítségével:
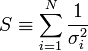
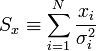
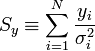
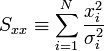
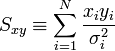
Így a minimum feltétele a következő:
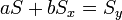
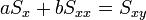
Az egyenletrendszer megoldása pedig:
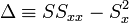
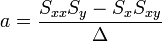
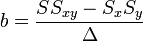
A hibaterjedés törvényét figyelembe véve a teljes szórás:
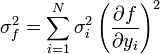
Amibe a-t és b-t behelyettesítve:
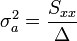
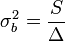
Ezek a hibák természetesen csak a mérési hibák hatását fejezik ki, ettől a pontok szórhatnak messze az egyenestől. Az illesztés jóságát az (N-2) szabadsági fokú khí-négyzet eloszlás adja meg a 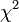 helyen.
helyen.
Ha a mérés hibája nem ismert, akkor a fenti képletek a 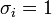 behelyettesítéssel használhatók (úgy tekintjük, hogy mindegyik pont hibája megegyezik).
behelyettesítéssel használhatók (úgy tekintjük, hogy mindegyik pont hibája megegyezik).