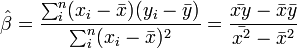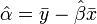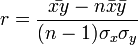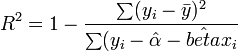Adatelemzés: lineáris és nem lineáris regresszió egy modellen bemutatva

Általános statisztikai jellemzők

Alapfogalmak:

• Átlag: ha van N darab adatpontunk (egy X vektorba rendezve), mindegyiket 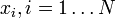$x_i, i = 1\ldots N$-vel jelöljük, akkor az átlag: $E[X] = \mu = \bar{x} = \frac{1}{N} \sum_{i=1}^N x_i$
• Szórás: ha van N db, 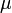$\mu$ átlagú adatpontunk, akkor ezek szórása: $\sigma = \sqrt{E\left[ X - \mu \right]^2}$
• Kovariancia: a kovariancia megadja két egymástól különböző változó (X,Y) együttmozgását: $Cov(X,Y) = E \left[ \left( X - E[X] \right) \left( Y - E[Y] \right) \right] = E[XY] - E[X]\cdot E[Y]$
• Kovariancia mátrix: egy n adatpontból álló X és egy m adatpontból álló Y véletlen (random) vektor n*m-es kovariancia mátrixa: $Cov(X,Y) = E\left[ \left( X - E[X] \right) \left( Y - E[Y] \right)' \right] = E[XY'] - E[X]E[Y]'$, ahol $E[XY']$, $E[Y]'$ és $E[X]$ vektorok és általános esetben mindegyik elemük az X és Y vektor eredeti elemének szórása (amennyiben a vektor komponensei különböző szórású valószínűségi változók).
• Keresztkorreláció: a keresztkorreláció segítségével megvizsgálhatjuk két adatsor hasonlóságát különböző időeltolásokra. Folytonos függvény esetén a definíció: 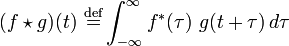$(f \star g)(t)\ \stackrel{\mathrm{def}}{=} \int_{-\infty}^{\infty} f^*(\tau)\ g(t+\tau)\,d\tau$, diszkrét adatpontok esetén pedig: $(f \star g)[n]\ \stackrel{\mathrm{def}}{=} \sum_{m=-\infty}^{\infty} f^*[m]\ g[n+m]$. Két fehér zaj függvény vagy vektor keresztkorrelációs függvénye egy Dirac-delta.
• Normált kereszt-korreláció:
• Autokorreláció:

(Átlag szórás, kovariancia...)

Modellek illesztése

Lineáris regresszió

A most leírt modell tulajdonságai a következők:

• prediktor változó: x
• az y-ok függetlenek
• adott x-re kapott y-ok normál eloszlásúak olyan átlaggal, ami az x lineáris függvényeként kapható meg

• Feladat: adott x-re y-t megmondani. A straight line regression model (egyenes vonal illesztő modell) alakja a köv:

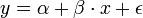$y = \alpha + \beta \cdot x + \epsilon$, vagy indexesen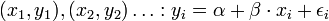 $(x_1, y_1), (x_2, y_2) \ldots: y_i = \alpha + \beta \cdot x_i + \epsilon_i$

A normál analízis során azt feltételezzük, hogy epsilon_i-k független és azonosan 0 átlagú és szigma^2 szórású normál eloszlást követő változók. Az alfa+beta*x a determinisztikus rész, az epsilon_i a random zaj. Az előbbi érdekel minket.

Az illesztés során a legkisebb négyzetek módszerét használhatjuk.

Legkisebb négyzetek módszere

A legkisebb négyzetek módszere bevezet egy metrikát arra nézve, hogy egy adott becslés az ismertelen 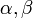$\alpha, \beta\,$ paraméterekre mennyire optimális. Ezt a mértéket következő költségfüggvény adja meg:

$\mathrm{min}_{\alpha, \beta}\left( \sum_{i=1}^N [y_i - \alpha - \beta x_i]^2 \right)$

azaz a legkisebb négyzetes eltérést eredményező paraméter értékeket keressük. Legegyszerűbben úgy találhatjuk meg ezt a minimumot, hogy a paraméterek szerint lederiváljuk a költségfüggvényt, és a kapott kifejezést 0-val tesszük egyenlővé, és a kapott egyenletrendszert megoldjuk. Az eredmény:

$\hat{\beta} = \frac{\sum_i^n ( x_i - \bar{x} )( y_i-\bar{y})}{\sum_i^n ( x_i - \bar{x} )^2} = \frac{\bar{xy} - \bar{x} \bar{y}}{\bar{x^2} - \bar{x}^2}$

$\hat{\alpha} = \bar{y} - \hat{\beta}\bar{x}$

ahol a felülvonás átlagolást jelent az n mérésen, a kalap pedig a módszer által adott becslést az adott paraméterre. Természetesen a levezetés általánosítható arra az esetre is, ha x több komponensű. Általánosabb költségfüggvényű módszerek is egyszerűen származtathatóak. Az x és y értékek korrelációját r adja:

$r = \frac{\bar{xy} - n\bar{x} \bar{y}}{(n-1)\sigma_x \sigma_y}$

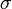ahol $\sigma$ a minta standard hibája. r értéke 1 ha tökéletes lineáris korreláció van, -1 ha tökéletes antikorreláció. A fit jóságát R^2 adja:

$R^2 = 1 - \frac{\sum (y_i - \bar{y})^2}{\sum (y_i - \hat{\alpha} - \hat{beta}x_i}$

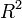$R^2$-et 1 ha tökéletesen lineárisak az adatok, általában a 0,95 körüli érték elfogadható fit szokott lenni.

A Khí-négyzet módszer

Ha a mérési pontok hibájának szórása nem egyforma (de továbbra is normál eloszlást követnek), akkor a legkisebb négyzetek módszerét könnyen általánosíthatjuk. Ez a Khí-négyzet illesztés, amelynek költségfüggvénye a következő:

$\chi^2 = \sum_{i=1}^N \left( \frac{y_i - \alpha - \beta x_i}{\sigma_i} \right)^2$

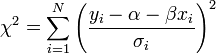
Tekinthetjük úgy, hogy a 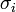$\sigma_i$ szórásokkal súlyozzuk az eltéréseket, vagy másképpen egységnyi szórásúra normálunk minden pontnál.

Mivel a mérési pontokról feltételeztük, hogy normál eloszlást követnek, 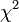$\chi^2$ ilyen véletlen változók négyzetének összege. Az ilyen típusú valószínűségi változók nem Gauss eloszlást, hanem az úgynevezett (N - M) szabadsági fokú Khí-négyzet eloszlást követik. Ha az 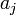$a_j$ paraméterek lineárisan szerepelnek akkor ez az eloszlás analitikusan megadható, így megmondható annak valószínűsége (Q), hogy az adott paraméterekkel jellemzett modellen végzett mérés 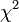$\chi^2$-nél nagyobb eltérést ad. (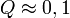$Q \approx 0,1$ tipikus, 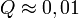$Q \approx 0,01$ elfogadható, 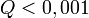$Q < 0,001$ rossz modellre vagy hibabecslésre utal). Fontos, hogy a mérési hibák becslése jó legyen, különben megtévesztő eredményre juthatunk.

A levezetés lépései teljesen azonosak az előző esettel.

Példa: egyenes illesztés

Legegyszerűbb példa a lineáris regresszióra a kétparaméteres egyenesillesztés.

$y(x) = a + bx\,$

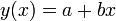
A költségfüggvényünk most:

$\chi^2(a,b) = \sum_{i=1}^N \left( \frac{y_i - a - bx_i}{\sigma_i} \right)^2$

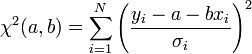
A minimumban a deriváltak eltűnnek:

$0 = \frac{\partial \chi^2}{\partial a} = -2\sum_{i=1}^N \frac{y_i - a - bx_i}{\sigma_i^2}$

$0 = \frac{\partial \chi^2}{\partial b} = -2\sum_{i=1}^N \frac{x_i(y_i - a - bx_i)}{\sigma_i^2}$

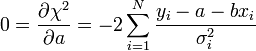
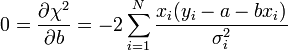
A fenti kifejezésekben a szummákat szétbonthatjuk az alábbi jelölések segítségével:

$S \equiv \sum_{i=1}^N \frac{1}{\sigma_i^2}$ $S_x \equiv \sum_{i=1}^N \frac{x_i}{\sigma_i^2}$ $S_y \equiv \sum_{i=1}^N \frac{y_i}{\sigma_i^2}$ $S_{xx} \equiv \sum_{i=1}^N \frac{x_i^2}{\sigma_i^2}$ $S_{xy} \equiv \sum_{i=1}^N \frac{x_iy_i}{\sigma_i^2}$

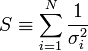
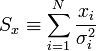
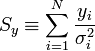
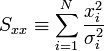
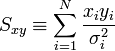
Így a minimum feltétele a következő:

$aS + bS_x = S_y$

$aS_x + bS_{xx} = S_{xy}$

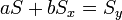
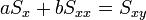
Az egyenletrendszer megoldása pedig:

$\Delta \equiv SS_{xx} - S_x^2$

$a = \frac{S_{xx}S_y - S_xS_{xy}}{\Delta}$

$b = \frac{SS_{xy}-S_xS_y}{\Delta}$

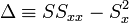
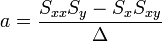
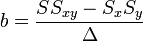
A hibaterjedés törvényét figyelembe véve a teljes szórás:

$\sigma_f^2 = \sum_{i=1}^N \sigma_i^2 \left( \frac{\partial f}{\partial y_i} \right)^2$

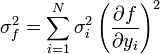
Amibe a-t és b-t behelyettesítve:

$\sigma_a^2 = \frac{S_{xx}}{\Delta}$

$\sigma_b^2 = \frac{S}{\Delta}$

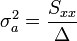
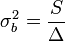
Ezek a hibák természetesen csak a mérési hibák hatását fejezik ki, ettől a pontok szórhatnak messze az egyenestől. Az illesztés jóságát az (N-2) szabadsági fokú khí-négyzet eloszlás adja meg a 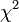$\chi^2$ helyen.

Ha a mérés hibája nem ismert, akkor a fenti képletek a 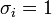$\sigma_i = 1$ behelyettesítéssel használhatók (úgy tekintjük, hogy mindegyik pont hibája megegyezik).

Maximum Likelihood

A maximum likelyhood a legvalószínűbb becslést adja egy tetszőleges eloszlás paramétereire. Ha 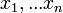$x_1, ...x_n$ megfigyelésünk van, és egy 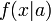$f(x|a)$ modellt szeretnénk fittelni, akkor a legjob