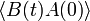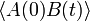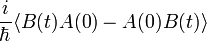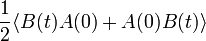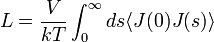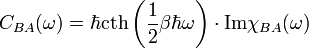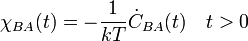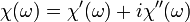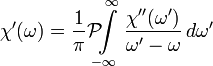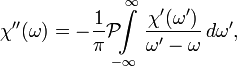Válasz- és korrelációs függvények, fluktuáció-disszipáció tétel
Ebbe a tételbe sok minden a Sasi-féle Nemegyensúlyi Statisztikus Fizika órából fog bekerülni.
Tartalomjegyzék
Lineáris válasz-elmélet
Kis külső perturbáció hatására a legkülönbözőbb fizikai rendszerek által produkált reakciók is jól tárgyalhatók lineáris közelítésben. Ide értendőek nem csak a korábban tárgyalt transzport jelenségek, de maguk a mérések is: például mechanikai vagy termodinamikai változásnak teszünk ki egy rendszert egy 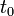 időpontban és megmérjük a különböző jellemzőit egy
időpontban és megmérjük a különböző jellemzőit egy 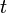 időpontban. A rendszert leíró fizikai jellemzők itt is első rendben lineáris kapcsolatba hozhatóak a perturbációval.
időpontban. A rendszert leíró fizikai jellemzők itt is első rendben lineáris kapcsolatba hozhatóak a perturbációval.
A tárgyaláshoz legyen az izolált (nem-perturbált) rendszer Hamiltonja 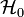 és a kölcsönhatást leíró Hamilton
és a kölcsönhatást leíró Hamilton 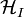 , valamint a teljes rendszert jellemző Hamilton ezek összege. Tételezzük fel a külső perturbációról nem csak azt, hogy gyenge, de azt is, hogy adiabatikusan kapcsoljuk be, azaz nagyon lassan, kvázi-stacionárius állapotokon keresztül.
, valamint a teljes rendszert jellemző Hamilton ezek összege. Tételezzük fel a külső perturbációról nem csak azt, hogy gyenge, de azt is, hogy adiabatikusan kapcsoljuk be, azaz nagyon lassan, kvázi-stacionárius állapotokon keresztül.
A rendszert jellemezzük a sűrűségoperátorral, 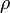 -val. Egy
-val. Egy 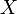 mennyiség átlaga (sokaság és kvantum átlag)
mennyiség átlaga (sokaság és kvantum átlag) 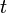 időpontban:
időpontban:
ahol 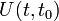 az időfejlesztés unitér operátora, amely leírja a rendszert jellemző mennyiségek időfejlődését
az időfejlesztés unitér operátora, amely leírja a rendszert jellemző mennyiségek időfejlődését 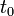 -ból
-ból 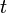 -be. A kölcsönhatási képben minden operátor (így
-be. A kölcsönhatási képben minden operátor (így 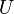 is) a szabad Hamilton szerint fejlődik időben:
is) a szabad Hamilton szerint fejlődik időben:
Ennek a megoldása 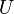 -ra egy exponenciális kifejezést ad, amit első rendig sorfejtve kapjuk, hogy:
-ra egy exponenciális kifejezést ad, amit első rendig sorfejtve kapjuk, hogy:
Ezt beírva az X mennyiség átlagának képletébe, és kihasználva a Tr ciklikusságát, valamint, hogy kezdetben a rendszer egyensúlyi állapotát a kanonikus eloszlás írta le: 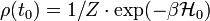 , továbbá a külső perturbációja legyen
, továbbá a külső perturbációja legyen 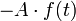 alakú, ahol
alakú, ahol 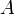 a perturbáló mennyiség operátora,
a perturbáló mennyiség operátora, 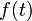 pedig a perturbáció amplitudója. Mindezekkel kapjuk:
pedig a perturbáció amplitudója. Mindezekkel kapjuk:
Mivel a Tr alatti ciklikus permutációs szimmetria van érvényben, az időfüggések átcsoportosíthatóak, ezért a []-es mennyiség csak az időkülönbségtől függ. Ezekkel kapjuk a Kubo-formulát:
ahol:
a szuszceptibilitás, vagy lineáris válasz függvény, a jobboldalon a második szögletes zárójel már kommutátort jelöl, a várhatóérték pedig a sokaságátlagot jelenti.
Nemegyensúlyi izoterm lineáris válsz
Ha nemegyensúlyi sokrészecskés kvantumrendszerre szeretnénk levezetni a lineáris választ (időfüggetlen, azaz sztatikus esetben), ahol nem ismert, hogy az állapotösszeg kicsit eltér az egyensúlyihoz képest, akkor ezt is sorfejteni kell a kölcsönhatás szerint. Itt most nem időfüggést vizsgálunk, hanem az egyensúlyi eloszlástól való eltérést. Eredményül azt kapjuk, hogy:
Itt az 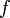 -et szorzó integrál
-et szorzó integrál 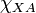 , az izoterm, sztatikus válaszfüggvény. A baloldali a nem-egyensúlyi (perturbált) várhatóértéke az X mennyiségnek, a jobboldali első tag az egyensúlyi várható érték. Ha akár a perturbáló, akár a rendszert jellemző operátor kommutál H-val, azaz megmaradó mennyiség, akkor az integrálból egy
, az izoterm, sztatikus válaszfüggvény. A baloldali a nem-egyensúlyi (perturbált) várhatóértéke az X mennyiségnek, a jobboldali első tag az egyensúlyi várható érték. Ha akár a perturbáló, akár a rendszert jellemző operátor kommutál H-val, azaz megmaradó mennyiség, akkor az integrálból egy 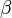 szorzó marad, ekkor a válaszfüggvény a korrelációs függvénnyel (alább az első def.) arányos, ez a fluktuáció-válasz tétel: tehát általánosan az izoterm lineáris válszt a korrelációs függvény
szorzó marad, ekkor a válaszfüggvény a korrelációs függvénnyel (alább az első def.) arányos, ez a fluktuáció-válasz tétel: tehát általánosan az izoterm lineáris válszt a korrelációs függvény 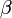 (inverz hőméréséklet) integrálja adja.
(inverz hőméréséklet) integrálja adja.
Lineáris válaszfüggvény és a transzport koefficiensek
Az egész elmélet azért is jelentős, mert a korábban tárgyalt transzport koefficiensek tulajdonképpen nem mások, mint a rendszer lineáris válaszai a megfelelő külső perturbációkra. Ennek megfelelően, például az elektromos vezetőre kapcsolt külső perturbáló tér esetén a váalszfüggvény a vezetőképesség tenzora lesz, ami így meghatározható a statsztikus átlagokból: a perturbáció operátora a polarizáció 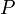 és a perturbáció amplitudója
és a perturbáció amplitudója 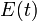 a külső elektromos tér, a rendszer válasza pedig az áramsűrűség. Ekkor az egyszerűség kedvéért izortop rendszerre:
a külső elektromos tér, a rendszer válasza pedig az áramsűrűség. Ekkor az egyszerűség kedvéért izortop rendszerre:
Korrelációs-függvények
Két mennyiség korrelációs függvényét igen sokféle alakban fel lehet írni. Például:
Belátható, hogy ezek közül csak 1 függtelen van. Az utolsó az alábbiakban még hivatkozott 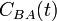 .
.
A korrelációs-függvények azért is fontosak, mert belőlük közvetlenül meghatározhatóak a lineáris transzport-koefficiensek. Ha 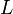 egy
egy 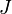 áramhoz tartozó transzport koefficiens, akkor a Green-Kubo formula alapján a kapcsolatuk:
áramhoz tartozó transzport koefficiens, akkor a Green-Kubo formula alapján a kapcsolatuk:
ahol a 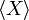 egyensúlyi átlag. Ezek a formulák csak egyensúlyi, végtelenül lassú (kvázistacionárius) folyamatokra érvényesek.
egyensúlyi átlag. Ezek a formulák csak egyensúlyi, végtelenül lassú (kvázistacionárius) folyamatokra érvényesek.
Fluktuáció-disszipáció tétel
A korrelációs-függvény és a lineáris válaszfüggvény között a Fourier-térben egyszerű alakú kapcsolat áll fent:
A korrelációs függvény az egyensúlyi fluktuációkat jellemzi, míg a lineáris válaszfüggvény képzetes része a rendszer irreverzibilis megváltozását (pl. disszipáció) jellemzi, amiközben törekszik az egyensúly felé.
Klasszikus határesetben azt kapjuk, hogy:
ahol a klasszikusság feltétele, hogy a rendszer átmenetei sokkal kisebb energiájúak legyenek, mint a hőmérsékleti fluktuációk jellemző energiái: 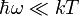
Ez a kapcsolat azést is fontos, mert a korrelációs-függvények aránylag könnyen mérhetők (pl: neutron-szórás kísérletek a nukleon-nukleon sűrűség korrelációs függvénnyel arányosak) ezáltal pedig megkaphatjuk a válaszfüggvény képzetes részét is. Magát a válszfüggvényt teljes egészében előállíthatjuk csupán a képzetes rész ismeretéből.
Kramers–Kronig-reláció
Matematikailag a Kramers–Kronig-reláció kapcsolatot teremt egy komplex függvény képzetes és valós része között, amennyiben a függvény analitikus a felső félsíkban. Fizikai rendszerek válaszfüggvényeinél a kauzalitás miatt ez a feltétel teljesül. A lineáris válszfüggvény Fourier-transzformáltja egy komplex mennyiség, írjuk fel tehát komplex alakban:
Ekkor a Kramers–Kronig-relációk:
és:
és 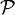 a főérték integrált jelöli.
a főérték integrált jelöli.
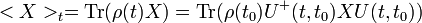
![i\hbar \frac{dU}{dt} = [U, \mathcal{H}_0]](/images/math/6/5/6/6560535c87f8094cac44301c2d173f61.png)
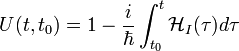
![\langle X \rangle_t = \langle X\rangle_0 + \frac{i}{\hbar}\int_{-\infty}^t d\tau \mathrm{Tr}\left[ \frac{\exp(-\beta\mathcal{H}_0)}{Z} (X(t)A(\tau)-A(\tau)X(t)) \right]f(\tau)](/images/math/a/a/e/aae87595587493a944327a00c350e75f.png)
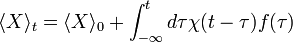
![\chi(t) = \frac{i}{\hbar}\mathrm{Tr}\left[ \frac{\exp(-\beta\mathcal{H}_0)}{Z} (X(t)A(0)-A(0)X(t)) \right]=\frac{i}{\hbar}\langle \left[ X(t), A(0) \right] \rangle_0](/images/math/d/a/a/daac7b8b42ad731d239dd50f8d959cb6.png)
![<X> = <X>_0 + \int_{0}^\beta ds \left[ \langle A(s)X \rangle_0 - \langle X \rangle_0 \langle A \rangle_0 \right] f](/images/math/a/7/8/a78248486c9bc37e80601a13ee5b4c53.png)
![\sigma(t) = \frac{1}{V} \chi_{JP}(t) = \frac{1}{V}\frac{i}{\hbar}\langle [J(t), P(0)] \rangle\,](/images/math/b/1/a/b1aec879ce2de0c0b5021362d79434b4.png)