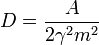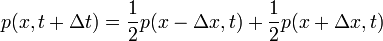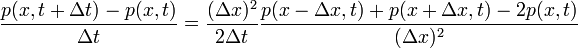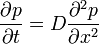„Transzportfolyamatok” változatai közötti eltérés
a (→Diffúzió - alternatív levezetés) |
a (→Transzport koefficiensek) |
||
| (12 közbenső módosítás ugyanattól a szerkesztőtől nincs mutatva) | |||
| 26. sor: | 26. sor: | ||
ahol | ahol | ||
| − | :<math>\mathbf{L}_{11} = e \int \frac{\partial f_0}{\partial E} \tau (\vec{v} \circ \vec{v}) d^3 p</math> | + | :<math>\mathbf{L}_{11} = e^2 \int \frac{\partial f_0}{\partial E} \tau (\vec{v} \circ \vec{v}) d^3 p</math> |
:<math>\mathbf{L}_{12} = \mathbf{L}_{21} = e \int \frac{\partial f_0}{\partial E} (E-E_F) \tau (\vec{v} \circ \vec{v}) d^3 p</math> | :<math>\mathbf{L}_{12} = \mathbf{L}_{21} = e \int \frac{\partial f_0}{\partial E} (E-E_F) \tau (\vec{v} \circ \vec{v}) d^3 p</math> | ||
| 33. sor: | 33. sor: | ||
| − | és <math>\circ</math> a diadikus szorzatot jelöli, <math>\tau</math> pedig az ütközési tag relaxációs idejét jelenti. Az L tenzor | + | és <math>\circ</math> a diadikus szorzatot jelöli, <math>\tau</math> pedig az ütközési tag relaxációs idejét jelenti. Az L tenzor szimmetrikus az Onsager-relációk miatt. Az Onsager-relációk szerint ha két termodinamikai erő hajtani tudja egymás áramait, akkor az ezekhez tartozó transzportkoefficiensek megegyeznek. Példaként ha egy folyadékot a hőmérséklet, nyomás és sűrűség jellemez, akkor a hőmáérséklet különbség hőáramot, a nyomáskülönbség anyagáramot hajt. Ha egyszerre van jelen hőmérsékletkülönbség és nyomáskülönbség akkor ezek is hajthatják a másik áramát, de az Onsager-relációk értelmében az egységnyi nyomáskülönbségre jutó hőáram és az egységnyi hőmérsékletkülönbség által hajtott sűrűségáram azonos. A tétel a mikroszkopikus rendszerek időtükrözési invarianciájából következik. |
| + | |||
| + | Ezek után a lineáris transzport koefficiensek tenzorai már egyszerűen felírhatóak: | ||
:<math>\mathbf{\sigma}_e = -e \mathbf{L}_{11}</math> azaz a vezetőképesség tenzora, ha nincs hőmérséklet gradiens. | :<math>\mathbf{\sigma}_e = -e \mathbf{L}_{11}</math> azaz a vezetőképesség tenzora, ha nincs hőmérséklet gradiens. | ||
| 41. sor: | 43. sor: | ||
A magasabb rendű és kereszteffektusok hasonlóan, csak bonyolultabb közelítések után számolhatóak, néhány példa: Peltier-, Thomson-, Seebeck együtthatók, Hall-tenzor stb. | A magasabb rendű és kereszteffektusok hasonlóan, csak bonyolultabb közelítések után számolhatóak, néhány példa: Peltier-, Thomson-, Seebeck együtthatók, Hall-tenzor stb. | ||
| − | Ezek az együtthatók egyébként közvetlenül is számolhatóak a mikroszkópikus modellekből, erről a Green–Kubo-összefügések adnak számot. | + | Ezek az együtthatók egyébként közvetlenül is számolhatóak a mikroszkópikus modellekből, erről a Green–Kubo-összefügések adnak számot (l. [[Válasz- és korrelációs függvények, fluktuáció-disszipáció tétel#Korrelációs-függvények|korrelációs-függvények]]). |
| + | |||
| + | ===Az elektromos vezetés Drude-modellje=== | ||
| + | Az elektromos vezetés jelenségét úgy tekintjük, hogy az elektronok az elektromos tér hatására gyorsulnak, azonban a vezető helyezkötött atomtörzseinek ütközve energiát veszítenek. Ez igen hamar makroszkópikus egyensúlyhoz vezet, ha a tér nem változik. Ezek a feltevések az alapjai a Drude-modellnek, amelynek eredménye az elektronokra felírható mozgásegyenlet: | ||
| + | |||
| + | :<math>m \ddot{x} = eE - m \frac{1}{\tau}v</math> | ||
| + | |||
| + | amelynek stacionárius megoldása: | ||
| + | |||
| + | :<math>m \frac{1}{\tau}v = eE </math> | ||
| + | |||
| + | Itt <math>\tau</math> az ütközések között eltellő jellemző relaxációs idő, ''v'' a drift sebesség. A ''v''-re rendezett eredményt a töltéssel (e) és az elektronsűrűséggel (n) beszorozva megkaphatjuk az Ohm-törvényt: | ||
| + | |||
| + | :<math>j = \frac{n e^2 \tau}{m}E</math> | ||
| + | |||
| + | azaz az elektromros áramsűrűség egyenesen arányos a térerősséggel, az arányossági tényező a fajlagos ellenállás reciproka, azaz a fajlagos vezetőképesség. A Drude-moell jó leírást ad több effektusra, azonban például az áram hőhatását túlbecsli. Kevés jó modell van az elektronok ütközésének leírására, ez a terület ma is aktív kutatás tárgya. | ||
| + | |||
== Diffúzió - alternatív levezetés == | == Diffúzió - alternatív levezetés == | ||
Az alábbiakban az erőmentes diffúzió egy levezetését adjuk. Ez felfogható a [[VélFiz 1.tétel|Fokker-Planck]] egyenlet egy másik levezetéseként is. Tekintsünk erőmentes rendszert, ekkor <math>F=0</math>, továbbá legyen jó közelítéssel homogén a közegünk. Úgy kell elképzelni, hogy egy sok kis részecséből álló egyensúlyban levő rendszerbe beteszünk kevés számú nagy tömegű részecskét. Ekkor a nagyok egymás közötti ütközéseit elhanyagolhatjuk, a kicsikkel való ütközésben viszont kevéssé változik meg az impulzusuk. Eredményként minden külcsönhatást az ütközési tagba írhatunk. Az előző feltételek miatt a Boltzmann-egyenletből csak az időderivált marad meg a baloldalon, így: | Az alábbiakban az erőmentes diffúzió egy levezetését adjuk. Ez felfogható a [[VélFiz 1.tétel|Fokker-Planck]] egyenlet egy másik levezetéseként is. Tekintsünk erőmentes rendszert, ekkor <math>F=0</math>, továbbá legyen jó közelítéssel homogén a közegünk. Úgy kell elképzelni, hogy egy sok kis részecséből álló egyensúlyban levő rendszerbe beteszünk kevés számú nagy tömegű részecskét. Ekkor a nagyok egymás közötti ütközéseit elhanyagolhatjuk, a kicsikkel való ütközésben viszont kevéssé változik meg az impulzusuk. Eredményként minden külcsönhatást az ütközési tagba írhatunk. Az előző feltételek miatt a Boltzmann-egyenletből csak az időderivált marad meg a baloldalon, így: | ||
| 94. sor: | 112. sor: | ||
Innen látszik, hogy a második deriváltas tag együtthatója <math>B</math>, tehát ez felel meg a diffúziós együtthatónak. | Innen látszik, hogy a második deriváltas tag együtthatója <math>B</math>, tehát ez felel meg a diffúziós együtthatónak. | ||
| − | == | + | ==A diffúzió Langevin modellje== |
| − | + | ||
| + | A langevin modellben egy <math>m</math> tömegű részecskét egy véletlenszerű erő lökdös, miközben surlódás is van a rendszerben. A megfelelő sztochasztikus differenciál-egyenlet: | ||
| + | |||
| + | :<math>m \dot v = -m \gamma v + \xi(t)</math> | ||
| + | |||
| + | Ennek a formális megoldása <math>v_0</math> kezdősebesség esetén: | ||
| + | |||
| + | :<math>v(t) = v_0 e^{-\gamma t} + \frac{e^{-\gamma t}}{m}\int_0^t d t' e^{\gamma t'} \xi(t')</math> | ||
| + | |||
| + | Ez nyilván nem érdekes fizikailag, sokkal inkább a sokaságátlag: ekkor a zaj eltűnik (attól zaj, hogy az átlaga zérus), és csak az exponenciálisan lecsengő kezdősebesség marad. A másik ami érdekes az a sebesség négyzetének átlaga: | ||
| + | |||
| + | :<math>\langle v^2(t) \rangle = v^2_0 e^{-2\gamma t} + 0 + \frac{e^{-2\gamma t}}{m^2}\int_0^t d t' \int_0^t d t'' e^{\gamma t'} e^{\gamma t''} \langle \xi(t')\xi(t'')\rangle</math> | ||
| + | |||
| + | ahol a vegyes tag a fenti átlag=0 feltétel miatt tűnt el. A zaj korrelációja az integrál alatt dirac delta, ezért egy integrálás elvégezhető, marad a zaj amplitudója: <math>A</math>, ezért végül: | ||
| + | |||
| + | :<math>\langle v^2(t) \rangle = v^2_0 e^{-2\gamma t} + \frac{A}{2\gamma m^2} \left( 1 - e^{-2\gamma t} \right)</math> | ||
| + | |||
| + | Kellően hosszú idő után, már csak a második tag marad meg. Ahhoz, hogy a diffúziós együtthatót levezethessük, az elmozdulás várhatóértékét kell felírnunk. Ez némi trükkel magából a Langevin-egyenletből megkapható (megszorozzuk x-el, és vesszük az egész egyenlet várhatóértékét. Eredményül azt kapjuk, hogy: | ||
| + | |||
| + | :<math>\langle x^2(t) \rangle = \langle[ \gamma t - 1 + e^{-\gamma t} \rangle] \frac{A}{\gamma^3 m^2}</math> | ||
| + | |||
| + | Kellően hosszú idő után a harmadik tag 0-hoz cseng le, a 2. pedig elhanyagolható az első mellett, ezért a diffúziós-együttható, ami definíció szerint 2t szorzófaktora: | ||
| + | |||
| + | :<math>D = \frac{A}{2\gamma^2 m^2}</math> | ||
| + | |||
| + | ==Általánosított diffúzió== | ||
| + | |||
| + | Ismert, hogy a rácson bolyongás problémája, ahol minden <math>\Delta t</math> lépésben egyet lépünk valamelyik véletlenszerűen kiválasztott <math>\Delta x</math> hosszú él mentén a kontinuum limeszben diffúziós folyamattal ekvivalens: példaként egydimenziós rácson a bolyongást a következő master-egyenlet írja le: | ||
| + | |||
| + | :<math>p(x, t+\Delta t) = \frac{1}{2}p(x-\Delta x, t) + \frac{1}{2}p(x+\Delta x, t)</math> | ||
| + | |||
| + | azaz annak a valószínűsége, hogy a részecskét az <math>t+1</math>-edik időpillanatban az <math>x</math> helyen találjuk azoknak a valószínűségeknek az összege, hogy előtte valamelyik szomszédos rácsponton volt. A lépések helyére differenciákat írva: | ||
| + | |||
| + | :<math>\frac{p(x, t+\Delta t) - p(x, t)}{\Delta t} = \frac{(\Delta x)^2}{2\Delta t} \frac{p(x-\Delta x, t) + p(x+\Delta x, t) - 2p(x, t)}{(\Delta x)^2}</math> | ||
| + | |||
| + | Elvégezve az infinitezimális limeszt, miközben <math>D = \frac{(\Delta x)^2}{2\Delta t}</math>-t konstanson tartjuk kapjuk, hogy: | ||
| + | |||
| + | :<math>\frac{\partial p}{\partial t} = D \frac{\partial^2 p}{\partial x^2}</math> | ||
| + | |||
| + | azaz a diffúziós egyenletet. Ez a bolyongásos megfogalmazás egyszerű általánosítási lehetőséget kínál: | ||
| + | |||
| + | Engedjük meg, hogy az időlépés is változhasson, legyen az eloszlása: <math>p(\Delta t) \propto \frac{1}{(\Delta t)^{1+\alpha}}</math> | ||
| + | Engedjük meg, hogy az távolságlépés is változhasson, legyen az eloszlása: <math>p(\Delta x) \propto \frac{1}{(\Delta x)^{1+\beta}}</math> | ||
| + | |||
| + | Amíg <math>\alpha > 1</math> és <math>\beta > 2</math> nem változik semmi, mert a várakozási idő átlaga is véges és a várható pozíció szórása is véges, ezért a centrális határeloszlás tétel következtében a gauss-os diffúziót kapjuk vissza. Ezeken kívül viszont változatos más viselkedéseket láthatunk: | ||
| + | |||
| + | # Lévi-repülés: <math>\alpha > 1</math>, <math>0 < \beta < 2</math>: <math>\bar{x} \propto t^{1 / \beta}</math> | ||
| + | # szubdiffúzió: <math>0 < \alpha < 1</math>, <math> \beta > 2</math>: <math>\bar{x} \propto t^{\alpha / 2}</math> | ||
| + | # ambvivalens folyamat: <math>0 < \alpha < 1</math>, <math>0 < \beta < 2</math>: <math>\bar{x} \propto t^{\alpha / \beta}</math> | ||
| + | |||
| + | Ilyen jellegű folyamatok sok helyen előfordulnak, például Lévi-repülés jellemzi az albatroszok repülését, míg az emberi utazási szokásokat egy <math>\alpha, \beta \propto 0.6</math> típusú ambvivalens folyamat írja le. | ||
| + | |||
| + | |||
{{MSc záróvizsga}} | {{MSc záróvizsga}} | ||
A lap jelenlegi, 2011. június 19., 10:50-kori változata
Az előző tételben bemutatott kinetikus egyenletek alapjául szolgáló eloszlásfüggvényekkel fejezhetőek ki a különböző makroszkopikusan is mérhető mennyiségek, illetve az ezek közötti kapcsolatok. Ezekről, illetve néhány egyszerű alkalmazásról lesz szó itt.
Tartalomjegyzék
A Boltzmann-típusú egyenletek momentumai
Annak analógiájára, hogy a sűrűségfüggvény integrálja a részecskeszámot adja, számos más mennyiség is előállítható belőle. Például tetszőleges 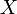 mennyiség áramsűrűsége:
mennyiség áramsűrűsége:
Ezzel könnyen felírható az elektromos töltés árama, vagy a hőáram (a Fermi-szint feletti energia árama):
Az átlagenergiasűrűséget már a sebesség második hatványával tudjuk kifejezni:
Látható, hogy a kifejezések integrandusában az 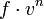 faktor a közös, ez alapján teljesen jogos a momentumokról beszélni, hiszen a sebesség egyre magasabb hatványai jelennek meg. Külön ki kell emelni, hogy mi a helyzet az ütközési tagok momentumatival. Általában plazma leírásnál felteszik, hogy ezeknek a momemtumai nullák, azaz nincs részecskeszám változás, nincs összenergia, illetve összimpulzus változás stb. Nyilván ezek csak bizonyos folyamatok esetében igazak, nem általános érvényességű igazságok (pl. ionizáció v rekombináció esetén változik a részecskeszám stb.), de mindig tükrözik, hogy az adott rendszerben milyen makroszkopikus megmaradási tételek igazak.
faktor a közös, ez alapján teljesen jogos a momentumokról beszélni, hiszen a sebesség egyre magasabb hatványai jelennek meg. Külön ki kell emelni, hogy mi a helyzet az ütközési tagok momentumatival. Általában plazma leírásnál felteszik, hogy ezeknek a momemtumai nullák, azaz nincs részecskeszám változás, nincs összenergia, illetve összimpulzus változás stb. Nyilván ezek csak bizonyos folyamatok esetében igazak, nem általános érvényességű igazságok (pl. ionizáció v rekombináció esetén változik a részecskeszám stb.), de mindig tükrözik, hogy az adott rendszerben milyen makroszkopikus megmaradási tételek igazak.
Transzport koefficiensek
A termodinamikai rendszert fizikai mennyiségek jellemzik. Ha egy ilyen mennyiségnek a lokális sűrűsége megváltozik, akkor ahhoz tartozik egy áram, ami az adott mennyiséget szállítja, ezeket a folyamatokat nevezzük transzport folyamatoknak. Ha az áram, illetve az áramot hajtó hatás nem túl nagy, akkor tipikusan jó a lineáris közelítés. Ekkor a lineáris együtthatót transzport koefficiensnek nevezzük. Néhány ilyen mennyiség például a hozzájuk tartozó áramokkal: Diffúziós-együttható (tömeg áram), viszkozitás (impulzus áram), hővezetési-együttható (energia áram), elektromos-vezetési együttható (az ellenállás reciproka, elektromos áram). Ezek kifejezhetőek a Boltzmann-egyenletekből megfelelő közelítések árán.
Példaképpen, ha csak az elektromos és hővezetési effektusokra szorítkozunk, akkor első közelítésben a következő egyenletek vezethetőek le:
ahol
és  a diadikus szorzatot jelöli,
a diadikus szorzatot jelöli, 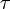 pedig az ütközési tag relaxációs idejét jelenti. Az L tenzor szimmetrikus az Onsager-relációk miatt. Az Onsager-relációk szerint ha két termodinamikai erő hajtani tudja egymás áramait, akkor az ezekhez tartozó transzportkoefficiensek megegyeznek. Példaként ha egy folyadékot a hőmérséklet, nyomás és sűrűség jellemez, akkor a hőmáérséklet különbség hőáramot, a nyomáskülönbség anyagáramot hajt. Ha egyszerre van jelen hőmérsékletkülönbség és nyomáskülönbség akkor ezek is hajthatják a másik áramát, de az Onsager-relációk értelmében az egységnyi nyomáskülönbségre jutó hőáram és az egységnyi hőmérsékletkülönbség által hajtott sűrűségáram azonos. A tétel a mikroszkopikus rendszerek időtükrözési invarianciájából következik.
pedig az ütközési tag relaxációs idejét jelenti. Az L tenzor szimmetrikus az Onsager-relációk miatt. Az Onsager-relációk szerint ha két termodinamikai erő hajtani tudja egymás áramait, akkor az ezekhez tartozó transzportkoefficiensek megegyeznek. Példaként ha egy folyadékot a hőmérséklet, nyomás és sűrűség jellemez, akkor a hőmáérséklet különbség hőáramot, a nyomáskülönbség anyagáramot hajt. Ha egyszerre van jelen hőmérsékletkülönbség és nyomáskülönbség akkor ezek is hajthatják a másik áramát, de az Onsager-relációk értelmében az egységnyi nyomáskülönbségre jutó hőáram és az egységnyi hőmérsékletkülönbség által hajtott sűrűségáram azonos. A tétel a mikroszkopikus rendszerek időtükrözési invarianciájából következik.
Ezek után a lineáris transzport koefficiensek tenzorai már egyszerűen felírhatóak:
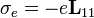 azaz a vezetőképesség tenzora, ha nincs hőmérséklet gradiens.
azaz a vezetőképesség tenzora, ha nincs hőmérséklet gradiens.![\mathbf{\sigma}_Q = \frac{1}{T}[ \mathbf{L}_{22} - \mathbf{L}_{12} (\mathbf{L}_{11})^{-1}\mathbf{L}_{12} ]](/images/math/a/3/3/a33d6b2b8f66cf61d98094598e50804c.png) a hővezetés tenzora, ha nincs elektromos áram.
a hővezetés tenzora, ha nincs elektromos áram.![\mathbf{S} = \frac{1}{T}[ (\mathbf{L}_{11})^{-1} \mathbf{L}_{12}]](/images/math/7/9/b/79b3790735c7bf86802753c4fae43892.png) a termoelektromos együttható, ha nincs elektromos áram.
a termoelektromos együttható, ha nincs elektromos áram.
A magasabb rendű és kereszteffektusok hasonlóan, csak bonyolultabb közelítések után számolhatóak, néhány példa: Peltier-, Thomson-, Seebeck együtthatók, Hall-tenzor stb.
Ezek az együtthatók egyébként közvetlenül is számolhatóak a mikroszkópikus modellekből, erről a Green–Kubo-összefügések adnak számot (l. korrelációs-függvények).
Az elektromos vezetés Drude-modellje
Az elektromos vezetés jelenségét úgy tekintjük, hogy az elektronok az elektromos tér hatására gyorsulnak, azonban a vezető helyezkötött atomtörzseinek ütközve energiát veszítenek. Ez igen hamar makroszkópikus egyensúlyhoz vezet, ha a tér nem változik. Ezek a feltevések az alapjai a Drude-modellnek, amelynek eredménye az elektronokra felírható mozgásegyenlet:
amelynek stacionárius megoldása:
Itt 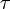 az ütközések között eltellő jellemző relaxációs idő, v a drift sebesség. A v-re rendezett eredményt a töltéssel (e) és az elektronsűrűséggel (n) beszorozva megkaphatjuk az Ohm-törvényt:
az ütközések között eltellő jellemző relaxációs idő, v a drift sebesség. A v-re rendezett eredményt a töltéssel (e) és az elektronsűrűséggel (n) beszorozva megkaphatjuk az Ohm-törvényt:
azaz az elektromros áramsűrűség egyenesen arányos a térerősséggel, az arányossági tényező a fajlagos ellenállás reciproka, azaz a fajlagos vezetőképesség. A Drude-moell jó leírást ad több effektusra, azonban például az áram hőhatását túlbecsli. Kevés jó modell van az elektronok ütközésének leírására, ez a terület ma is aktív kutatás tárgya.
Diffúzió - alternatív levezetés
Az alábbiakban az erőmentes diffúzió egy levezetését adjuk. Ez felfogható a Fokker-Planck egyenlet egy másik levezetéseként is. Tekintsünk erőmentes rendszert, ekkor 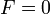 , továbbá legyen jó közelítéssel homogén a közegünk. Úgy kell elképzelni, hogy egy sok kis részecséből álló egyensúlyban levő rendszerbe beteszünk kevés számú nagy tömegű részecskét. Ekkor a nagyok egymás közötti ütközéseit elhanyagolhatjuk, a kicsikkel való ütközésben viszont kevéssé változik meg az impulzusuk. Eredményként minden külcsönhatást az ütközési tagba írhatunk. Az előző feltételek miatt a Boltzmann-egyenletből csak az időderivált marad meg a baloldalon, így:
, továbbá legyen jó közelítéssel homogén a közegünk. Úgy kell elképzelni, hogy egy sok kis részecséből álló egyensúlyban levő rendszerbe beteszünk kevés számú nagy tömegű részecskét. Ekkor a nagyok egymás közötti ütközéseit elhanyagolhatjuk, a kicsikkel való ütközésben viszont kevéssé változik meg az impulzusuk. Eredményként minden külcsönhatást az ütközési tagba írhatunk. Az előző feltételek miatt a Boltzmann-egyenletből csak az időderivált marad meg a baloldalon, így:
A jobboldalra tegyük fel a következő Master-egyenletet, amiben a 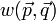 átmeneti valószínűség jellemi az ütközési folyamatban a
átmeneti valószínűség jellemi az ütközési folyamatban a 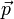 impulzusról
impulzusról 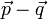 -ra történő változás egységnyi időre jutó rátáját. Ekkor:
-ra történő változás egységnyi időre jutó rátáját. Ekkor:
Az, hogy a nagy részecske impulzusa cska kicsit áltozik meg a kisebbekel való ütközésben úgy jelenik meg, hogy 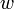 függvény gyorsan csökken
függvény gyorsan csökken 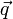 -ban, ezért
-ban, ezért 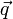 -t kicsinek vehetjük, és sorfejthetünk:
-t kicsinek vehetjük, és sorfejthetünk:
Ekkor a kinetikus egyenletünk a következő alakba írható, amit Fokker-Planck egyenletnek neveznek::
ahol:
A Fokker-Planck-egyelet jobboldalára tekinthetünk úgy, mint egy divergenciára, ami ekkor a részecskeszám megmaradását fejezi ki. Az ehhez tartozó megmaradó áram (Noeter-tétel!) a részecskeszám-áramsűrűség:
A jobboldal első két tagjára bevezethetjük a 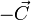 jelölést. Egyensúlyban az áram nulla, és ha azt is kihasználjuk, hogy ekkor
jelölést. Egyensúlyban az áram nulla, és ha azt is kihasználjuk, hogy ekkor  , ahol
, ahol 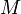 a nehéz részecske tömege,
a nehéz részecske tömege, 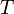 pedig a háttér kis részecskék hőmérséklete, akkor
pedig a háttér kis részecskék hőmérséklete, akkor 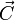 és
és 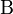 nem függetlenek:
nem függetlenek:
Ezzel a mozgásegyenlet alakja:
Ha még azt a közelítést is alkalmazzuk, hogy a nehéz részecskék visszalökődése elhanyagolható, akkor 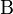 impulzusfüggetlen lesz, és egyetlen skalárral (
impulzusfüggetlen lesz, és egyetlen skalárral (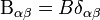 ) reprezentálható:
) reprezentálható:
Az 1/3 faktor onnan jött, hogy összegeztünk az indexekre és 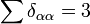 . Így a mozgásegyenlet:
. Így a mozgásegyenlet:
Innen látszik, hogy a második deriváltas tag együtthatója 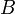 , tehát ez felel meg a diffúziós együtthatónak.
, tehát ez felel meg a diffúziós együtthatónak.
A diffúzió Langevin modellje
A langevin modellben egy 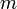 tömegű részecskét egy véletlenszerű erő lökdös, miközben surlódás is van a rendszerben. A megfelelő sztochasztikus differenciál-egyenlet:
tömegű részecskét egy véletlenszerű erő lökdös, miközben surlódás is van a rendszerben. A megfelelő sztochasztikus differenciál-egyenlet:
Ennek a formális megoldása 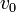 kezdősebesség esetén:
kezdősebesség esetén:
Ez nyilván nem érdekes fizikailag, sokkal inkább a sokaságátlag: ekkor a zaj eltűnik (attól zaj, hogy az átlaga zérus), és csak az exponenciálisan lecsengő kezdősebesség marad. A másik ami érdekes az a sebesség négyzetének átlaga:
ahol a vegyes tag a fenti átlag=0 feltétel miatt tűnt el. A zaj korrelációja az integrál alatt dirac delta, ezért egy integrálás elvégezhető, marad a zaj amplitudója: 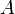 , ezért végül:
, ezért végül:
Kellően hosszú idő után, már csak a második tag marad meg. Ahhoz, hogy a diffúziós együtthatót levezethessük, az elmozdulás várhatóértékét kell felírnunk. Ez némi trükkel magából a Langevin-egyenletből megkapható (megszorozzuk x-el, és vesszük az egész egyenlet várhatóértékét. Eredményül azt kapjuk, hogy:
Kellően hosszú idő után a harmadik tag 0-hoz cseng le, a 2. pedig elhanyagolható az első mellett, ezért a diffúziós-együttható, ami definíció szerint 2t szorzófaktora:
Általánosított diffúzió
Ismert, hogy a rácson bolyongás problémája, ahol minden 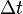 lépésben egyet lépünk valamelyik véletlenszerűen kiválasztott
lépésben egyet lépünk valamelyik véletlenszerűen kiválasztott 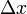 hosszú él mentén a kontinuum limeszben diffúziós folyamattal ekvivalens: példaként egydimenziós rácson a bolyongást a következő master-egyenlet írja le:
hosszú él mentén a kontinuum limeszben diffúziós folyamattal ekvivalens: példaként egydimenziós rácson a bolyongást a következő master-egyenlet írja le:
azaz annak a valószínűsége, hogy a részecskét az 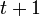 -edik időpillanatban az
-edik időpillanatban az 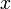 helyen találjuk azoknak a valószínűségeknek az összege, hogy előtte valamelyik szomszédos rácsponton volt. A lépések helyére differenciákat írva:
helyen találjuk azoknak a valószínűségeknek az összege, hogy előtte valamelyik szomszédos rácsponton volt. A lépések helyére differenciákat írva:
Elvégezve az infinitezimális limeszt, miközben 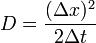 -t konstanson tartjuk kapjuk, hogy:
-t konstanson tartjuk kapjuk, hogy:
azaz a diffúziós egyenletet. Ez a bolyongásos megfogalmazás egyszerű általánosítási lehetőséget kínál:
Engedjük meg, hogy az időlépés is változhasson, legyen az eloszlása: 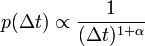 Engedjük meg, hogy az távolságlépés is változhasson, legyen az eloszlása:
Engedjük meg, hogy az távolságlépés is változhasson, legyen az eloszlása: 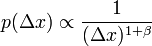
Amíg  és
és 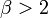 nem változik semmi, mert a várakozási idő átlaga is véges és a várható pozíció szórása is véges, ezért a centrális határeloszlás tétel következtében a gauss-os diffúziót kapjuk vissza. Ezeken kívül viszont változatos más viselkedéseket láthatunk:
nem változik semmi, mert a várakozási idő átlaga is véges és a várható pozíció szórása is véges, ezért a centrális határeloszlás tétel következtében a gauss-os diffúziót kapjuk vissza. Ezeken kívül viszont változatos más viselkedéseket láthatunk:
- Lévi-repülés:
 ,
, 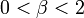 :
: 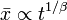
- szubdiffúzió:
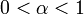 ,
, 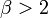 :
: 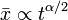
- ambvivalens folyamat:
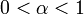 ,
, 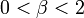 :
: 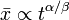
Ilyen jellegű folyamatok sok helyen előfordulnak, például Lévi-repülés jellemzi az albatroszok repülését, míg az emberi utazási szokásokat egy 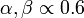 típusú ambvivalens folyamat írja le.
típusú ambvivalens folyamat írja le.
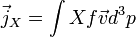
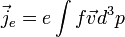
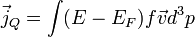
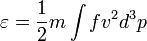
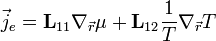
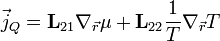
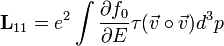
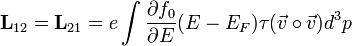
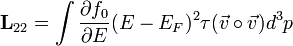
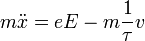
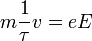
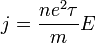
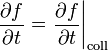
![\left. \frac{\partial f}{\partial t} \right|_{\mathrm{coll}} = \int [w(\vec{p}+\vec{q}, \vec{q})f(t, \vec{p}+\vec{q}) - w(\vec{p}, \vec{q})f(t, \vec{p})] d^3q](/images/math/1/2/2/122832de6a2d4a0c8e797735d836f43b.png)
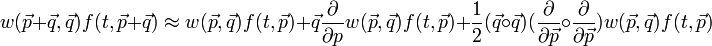
![\frac{\partial f}{\partial t} = \frac{ \partial}{\partial p_{\alpha}} \left( A_{\alpha}f + \frac{ \partial}{\partial p_{\beta}} [\mathrm{B}_{\alpha\beta} f]\right)](/images/math/7/2/1/72113ff18cccf92d1abfc6ef95422bae.png)

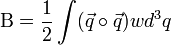
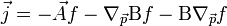
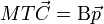
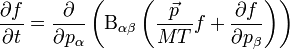
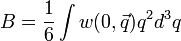
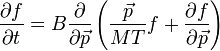
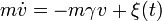
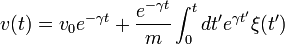
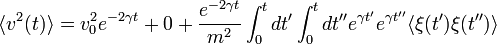
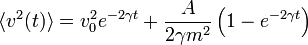
![\langle x^2(t) \rangle = \langle[ \gamma t - 1 + e^{-\gamma t} \rangle] \frac{A}{\gamma^3 m^2}](/images/math/9/b/8/9b822463e8f399b0b4aa3980cde6da60.png)