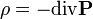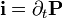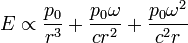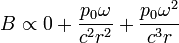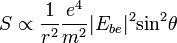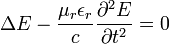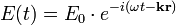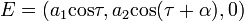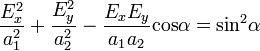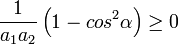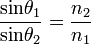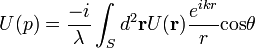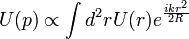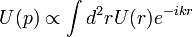„Hullámegyenlet és hullámoptika” változatai közötti eltérés
(Új oldal, tartalma: „==Az elektromágneses hullámegyenletek== A változó elektromos tér, mint tudjuk, mágneses teret kelt, a változó mágneses tér elektormos teret kelt. Ebből érezhet…”) |
a |
||
| (2 közbenső módosítás, amit egy másik szerkesztő végzett, nincs mutatva) | |||
| 50. sor: | 50. sor: | ||
==Hullámok terjedése, Doppler-effektus== | ==Hullámok terjedése, Doppler-effektus== | ||
| − | Mint láttuk a gömbhullám megoldásban <math>1/r</math>-es lecsengés van jelen, ebből kifolyólag a szállított energia (amit a Poynting-vektor ad meg | + | Mint láttuk a gömbhullám megoldásban <math>1/r</math>-es lecsengés van jelen, ebből kifolyólag a szállított energia (amit a Poynting-vektor ad meg és az <math>S = E \times B</math> képlettel lehet kiszámolni) <math>1/r^{2}</math>-es lecsengést mutat. |
A klasszikus hullámjelenségekhez hasonlóan az elektromágneses hullámoknál is frekvenciaeltolodás lép fel ha a forrás és az észlelő egymáshoz képest mozognak. Ha közelednek egymás felé, akkor az észlelt frekvencia nagyobb, ha távolodnak, akkor kisebb a kibocsájtottnál. | A klasszikus hullámjelenségekhez hasonlóan az elektromágneses hullámoknál is frekvenciaeltolodás lép fel ha a forrás és az észlelő egymáshoz képest mozognak. Ha közelednek egymás felé, akkor az észlelt frekvencia nagyobb, ha távolodnak, akkor kisebb a kibocsájtottnál. | ||
A lap jelenlegi, 2014. június 25., 09:10-kori változata
Tartalomjegyzék
- 1 Az elektromágneses hullámegyenletek
- 2 Elektromágneses hullámok előállítása, a Hertz-kísérlet
- 3 Hullámok terjedése, Doppler-effektus
- 4 Hullámok jellemzői
- 5 Retardált és avanzsált potenciálok
- 6 Hullámvezetők, és üregrezonátorok
- 7 Antennák, dipólsugárzás
- 8 Szóródás
- 9 Hullámoptika, polarizáció
- 10 Diffrakció
- 11 Fourier-optika
- 12 Nemlineáris optika alapjai
Az elektromágneses hullámegyenletek
A változó elektromos tér, mint tudjuk, mágneses teret kelt, a változó mágneses tér elektormos teret kelt. Ebből érezhető, hogy ez egy önmagát fenntartó folyamat tud lenni, amelyet az időben tovaterjedő változás jellemez.
Származtatás a Maxwell-egyenletekből
Ismertek a teljes Maxwell-egyenletek:
Vegyünk egy töltés és árammentes térrészt. Ekkor az első egyenlet jobboldalának második tagja, és a második egyenlet jobboldala nulla lesz. Osszuk le az átalakított első egyenletet 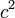 -el, és vegyük a rotációját. A baloldal ekkor:
-el, és vegyük a rotációját. A baloldal ekkor:
Itt kihasználtuk a negyedik Maxwell egyenletet, valamint egy vektoranalitikai azonosságot. A rotációt a jobboldalon is elvégezve a következő egyenletet kapjuk (figyelem, a rot helyszerinti deriválást tartalmaz, az időderiválással felcserélhető!):
Itt behelyettesíthetjük a harmadik Maxwell-egyenletet, és ekkor homogén hullámegyenletet kapunk B-re:
Teljesen analóg módon levezethető E-re is:
A hullámegyenlet megoldásai
Két alapvetően különböző megoldása van a hullámegyenleteknek: síkhullám és gömbhullám.
A síkhullám megoldás
Ez a megoldás azért síkhullám megoldás, mert a hullámhoz tartozó térmennyiség egy sík mentén veszi fel adott pillanatban az azonos értékeit. Tehá ezeken a helyeken a térmennyiség argumentuma ugyan az. Tehát az általános alakú hullámegyenlet és síkhullám megoldása a következő:
Természetesen a megoldás egy konstans amplitúdóval megszorozható tetszés szerint. Belátható, hogy az időszerinti második derivált megegyezik f argumentum szerinti második deriváltjával (itt kihasználjuk, hogy n egységnyi hosszú), továbbá ez valóban kielégíti a hullámegyenletet. Ha a megoldást, a térmennyiségekre felírva a Maxwell-egyenletekbe visszaírjuk, akkor kiderül, hogy n, E, B, páronként merőleges, azaz az elektromágneses hullám transzverzális.
A gömbhullám megoldás
Ekkor a megoldást polárkoordinátákban érdemes felírni, ennek megfelelően a Laplace-operátort is polárkoordinátás alakban kell tekinteni (bár abból csak a sugárfüggő részre van szükségünk).
Elektromágneses hullámok előállítása, a Hertz-kísérlet
Maxwell csak elméletileg jósolta meg az elektromágneses hullámok létezését, azonban Hertz-nek sikerült kísérletileg is kimutatnia őket. A kísérletekben Hertz dipólantennákat használt adóként, vevőként, illetve szikraközökkel láthatóvá is tudta tenni a hullámok által a forrástól távolabb okozott változásokat.
A dipólantenna azóta is alapvető eleme a hullámtechnikának. Ez tulajdonképpen egy váltóárammal táplált szétnyitott kondenzátor. A benne oda-vissza mozgó töltések keltik az elektromágneses hullámokat.
Hullámok terjedése, Doppler-effektus
Mint láttuk a gömbhullám megoldásban 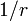 -es lecsengés van jelen, ebből kifolyólag a szállított energia (amit a Poynting-vektor ad meg és az
-es lecsengés van jelen, ebből kifolyólag a szállított energia (amit a Poynting-vektor ad meg és az 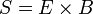 képlettel lehet kiszámolni)
képlettel lehet kiszámolni) 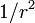 -es lecsengést mutat.
-es lecsengést mutat.
A klasszikus hullámjelenségekhez hasonlóan az elektromágneses hullámoknál is frekvenciaeltolodás lép fel ha a forrás és az észlelő egymáshoz képest mozognak. Ha közelednek egymás felé, akkor az észlelt frekvencia nagyobb, ha távolodnak, akkor kisebb a kibocsájtottnál.
Hullámok jellemzői
A hullámokat két fontos jellemző fizikai mennyiség jellemzi a fázis és a csoportsebesség. A definíciók:
Az elektromágneses hullámok csoportsebességére kell teljesülnie annak, hogy az adott közegbeli fénysebességgel terjednek. A fázissebesség ettől igen eltérő is lehet, akár több is, mint a csoportsebesség. Igen szemléletes az ábra itt!
A fenti jellemzők csak kevés információt adnak a hullámok terjedéséről. A közeg törésmutatója függhet a frekvenciától, így a terjedési sebességek is változhatnak attól függően, hogy milyen frekvenciájú hullámot vizsgálunk. A hullám terjedését homogén közegben legjobban az 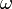 - k összefüggés, másnéven a diszperziós függvény jellemzi. Ez határozza meg, hogy adott hullámszámú hullám milyen frekvenciájú. Ha az anyag nem homogén (anizotrop), akkor a diszperzió lehet irányfüggő is.
- k összefüggés, másnéven a diszperziós függvény jellemzi. Ez határozza meg, hogy adott hullámszámú hullám milyen frekvenciájú. Ha az anyag nem homogén (anizotrop), akkor a diszperzió lehet irányfüggő is.
Fontos továbbá, hogyha a részecskéket is hullámként kezeljük de Brogile hipotézise értelmében akkor a diszperziós-reláció az energia és az impulzus kapcsolataként jelenik meg.
Retardált és avanzsált potenciálok
Tekintsük a negyedik Maxwell-egyenletet. Ha egy térmennyiség divergenciája nulla, akkor az valamilyen másik térmennyiség rotációjaként írható fel (legalábbis gömbbel topológiailag izomorf struktúrán, 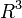 -ban). Ezért bevezetjük az A vektorpotenciált:
-ban). Ezért bevezetjük az A vektorpotenciált:
Ha ezt visszaírjuk a harmadik Maxwell-egyenletbe, akkor abban két rotáció fog szerepelni, melyeket összevonhatunk, így:
Ha egy vektormező rotációja nulla, akkor az a mező felírható egy skalártér negatív gradienseként, ezért bevezetünk egy skalárpotenciált is:
Ez átrendezve:
A két potenciált együtt elektromágneses potenciáloknak nevezzük. Megjegyzendő, hogy ezekben van egy mértékszabadság a következő transzformációra:
Azaz, ugyanahhoz az elektromágneses B és E térerősségekhez tetszőleges 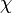 tartozhat, másképp fogalmazva a Maxwell-egyeneltek a fenti mértéktranszformációra invariánsak. A bevezetett potenciálokat a töltés és áramelrendezés meghatározza. Mivel a fenti mértékválasztás tetszőleges, ezért célszerű olyan mértéket választani, ahol a potenciálokat meghatározó egyenletek a legegyszerűbbek. Erre a Lorentz-feltétel alkalmas (ennek nincs fizikai jelentése, csak a számolást teszi egyszerűbbé):
tartozhat, másképp fogalmazva a Maxwell-egyeneltek a fenti mértéktranszformációra invariánsak. A bevezetett potenciálokat a töltés és áramelrendezés meghatározza. Mivel a fenti mértékválasztás tetszőleges, ezért célszerű olyan mértéket választani, ahol a potenciálokat meghatározó egyenletek a legegyszerűbbek. Erre a Lorentz-feltétel alkalmas (ennek nincs fizikai jelentése, csak a számolást teszi egyszerűbbé):
Ekkor a következő differenciálegyenletek vezethetők le a Maxwell-egyenletekből:
Itt i az áramsűrűség, 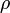 a töltéssűrűség. Az ilyen típusú differenciálegyenleteket d'Alembert típusúaknak nevezzük, belátható, hogy megoldásuk:
a töltéssűrűség. Az ilyen típusú differenciálegyenleteket d'Alembert típusúaknak nevezzük, belátható, hogy megoldásuk:
Ezek a formulák úgy értelemzhetőek, hogy egy adott r pontban mérhető potenciálok értékeit a tér többi pontjában található töltés- és áramelrendezés határozza meg, DE nem az ugyanazon pillanatbeli, hanem a közegbeli fénysebesség szerinti idővel korábbi állapot által létrehozott. Másképp megfogalmazva, ha egy töltést valahol megmozdítunk, akkor annak hatása, csupán a közegbeli fénysebességgel terjed, ezért a változás késve észlelhető csak távolabbról. Az itt felírt, ilyen tulajdonságú potenciálokat retardált potenciáloknak nevezzük. A d'Alembert egyenleteknek egy másik formális megoldását kapjuk akkor is, ha a fenti egyenletekben az időfüggésben megfordítjuk a pozitív előjelet negatívra. Ezek az avanzsált potenciálok Ebben az esetben az adott pillanatbeli potenciálokat a későbbi töltés és áramelrendezés határozzná meg, ez fizikailag azonban általában nem releváns megoldás.
Hullámvezetők, és üregrezonátorok
Mint tudjuk a vezetők belsejében az elektromos és mágneses térerősség nulla, továbbá a térerősség a felületen merőlegesen fog mutatni (feltettük, hogy a határ másik felén szigetelő van). Ha valamilyen változás van, és azt a töltések követni tudják, akkor úgy tekinthetjük őket, hogy olyan áramokat és töltéselrendezést hoznak létre, hogy a fentiek továbbra is teljesüljenek. Az ismert térerősségek a felületekben exponenciális lecsengést mutatnak. Az erre jellemző karakterisztikus hossz a behatolási mélység, ez függ a változás frekvenciájától, és a vezetőképességtől is. Az időben változó terek azonban kicsi, de véges érintő irányú teret is adnak az elektormos térnek, ez felelős a Joule-hőveszteségért.
Hullámvezetőnek nevezzük az olyan üreges elektromosan vezető anyagból készült csövet, ami két végén nyitott, így a hullámok tudnak benne haladni. Ha le van zárva a két vége is, akkor üregrezonátorról beszélünk. Ezeknek megfelelően a megoldásokat a hosszanti szimmetria tengely (z) mentén haladó, vagy álló síkhullámok alakjában kereshetjük. A határfeltételeken az előzőekben ismertetett effektusokkra is figyelni kell, de a hőveszteségtől most eltekintünk. A hullámegyenlet összefoglalva a következő alakú lesz:
Figyelembe véve a határfeltételeket (Az E z komponense a felületen 0, a B z komponensének normális irányú deriváltja szintén 0) sajátértékegyenletet kapunk. Azt mondhatjuk, hogy a felület teljes hosszára kirótt határfeltétel megkvantálja a megoldásokat, azaz adott frekvenciához csak diszkrét hullámszámok megengedettek. Mivel eltérőek a határfeltétlek a két térre, ezért általában különbözők a sajátértékek is a két térre, ez két féle kategóriát jelent a megoldásoknak: Transzverzális Mágneses hullámokról, illetve Transzverzális Elektromos hullámokról beszélhetünk. A megoldásoknál az vehető észre, hogy a megengedett frekvenciánál kisebb frekvenciájú hullámok lecsengenek, és csak a megengedett és annál nagyobb frekvenciájú, hullámok tudnak benne terjedni, ezkből azonban véges sok van, az előző kvantálási okokból kifolyólag. Ez a jelenség igen fontos a telekommunikációban.
Hasonlóan egy megfelelően elkészített üregrezonátort, ha elkezdünk rezgetni, akkor az is csak diszkrét frekvenciákat tart meg, a többi lecseng, így kiválóan alkalmas frekvenciák kiválasztására és erősítésére. Egy igen fontos üregrezonátort alkot a Föld az ionoszférával. Ezt a rezonátort példul a villámlások gerjesztik, és ezek hatása igen éles csúcsok jelentkeznek a zajspektrumban, amelyek jól leírhatóak elméleti alapon. Továbbá ezek a frekvenciák érzékenyek bizonyos globális változásokra, így például az éghajlatváltozásra.
Antennák, dipólsugárzás
Vegyünk egy időben periódikusan változó dipólt, amely például a Hertz-féle dipólantenna is lehet. Kíváncsiak vagynk arra, hogy a térerősség hogyan változik időben, különböző távolságokra az antennától. A töltéssűrűséget és az áramsűrűséget egyszerőenszármaztathatjuk a dipólsűrűségből:
Ezekután a fentieket behelyettesítjük a retardált potenciálokba, és a korábban kifejezett elektromos és mágneses térerősséget deriválásokkal kiszámítjuk belőlük. Az eredményből a nagyságrendek érdekesek, ha a rezgő dipól fekvenciája 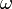 :
:
Az elektormos térerősség tagjai: sztatikus dipól tere + polarizációs áram tere + sugárzási (kifutó gömbhullám) tér. A mágneses indukció tagjai: áram mágneses tere + kifutó gömbhullám.
Ha felírjuk E és B komponenseit, látható, hogy mindkettő szögfüggő, azonban a Poynting vektor, amely a kettőre merőleges, radiális lesz, azaz a kisugrázott energia radiálisan terjed tova, továbbá S abszolut értéke 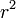 szerint cseng le, azonban még ez a mennyiség is szögfüggő: a dipól irányában minimális (0), attól 90 fokban oldalt maximális a kisugárzott energia mértéke.
szerint cseng le, azonban még ez a mennyiség is szögfüggő: a dipól irányában minimális (0), attól 90 fokban oldalt maximális a kisugárzott energia mértéke.
Szóródás
Elektromágneses szóródás akkor jön létre, amikor egy töltésrendszerre elektromágneses hullám érkezik, és az megrezgeti a töltéseket (p elektromos, és m mágneses dipólusokat indukál). Ekkor a mozgó töltések rezgésbe jönnek, és maguk is sugározni kezdenek (dipólsugárzás ez is). Ennek eredményeként a bejövő sugárzás energiájának egy része a beeséstől különböző irányban kerül kisugárzásra. Az összes energia azonban megmarad, így rugalmas szórásról beszélhetünk. Ha ezek a szórócentrumok a hullámhosszhoz képest kis méretűek, akkor Rayleigh-féle szórásról beszélünk. Tetszőleges méretre a Mie-féle szóráselmélet ad leírást, ennek speciális esete a Rayleigh-féle leírás.
Szóródás szabad töltésen
Itt is a dipólsűrűséget írjuk be a retardált potenciálokba, és kiszámoljuk az elektromos térerősséget, és a mágneses indukciót, majd ezekből a Poyinting-vektort. Az erdmény:
Szóródás töltött gömbön, avagy miért kék az ég
Ahogy láttuk a dipólsugárzásnál, a kifutógömbhullám E-je és B-je is a frekvencia négyzetével arányos, ez azt jelenti, hogy a kisugárzott S a frekvencia negyedik hatványával arányos. Egy adott térrészben kisugrázott energia és az elnyelt energia hányadosából kiszámítható a hatáskeresztmetszet. Ezt felintegrálva a teljes hatáskeresztmetszet megkapható, ebben változatlanul a negyedik hatványon fog szerepelni a frekvencia. Ez azt jelenti, hogyha kétszer nagyobb frekvenciájú (fele akkora hullámhosszú) hullámot szórunk, akkor az eltérülés valószínűsége 16-szor lesz nagyobb. A látható spektrumban a kék hullámhossza közel fele a vörös hullámhosszának ( kb 380 és 750 nm), tehát a kék fény lényegesen jobban szóródik, míg a vörös gyakorlatilag megtartja korábbi irányát. Ezért dominál a kék szín az égbolton, és ezért vörös a naplemente (hátha még a városi szmog is odakerül).
Hullámoptika, polarizáció
Tekintsük a szabad hullámegyenletet dielektrikumban:
Ennek megoldása egy periodikus síkhullám:
Legyen k z irányú, és jelölje 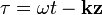 . Ekkor E vetülete az x-y síkban egy másodrendű görbét definiál:
. Ekkor E vetülete az x-y síkban egy másodrendű görbét definiál:
Ez egy kúpszelet egyenlete, hogy milyen azt a következő formula adja meg:
Ha a szög 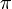 egész számú többszöröse, akkor a görbe egy egyenes párt alkot, ekkor beszélünk lineáris polarizációról. Ha a szög 90-foknak páratlan többszöröse, és a két méretszorzó egyezik, akkor cirkuláris a polarizáció. Egyéb esetben általános, elliptikus polarizációról beszélünk. Az elektromágneses hullám polarizációja befolyásolja a kölcsönhatását a határfelületekkel, és az optikailag aktív közegekkel. A közegben terjedő változásokat a közegbeli Maxwell-egyenletekből számolhatjuk, a határfelületeken a határfelületi törvényeket kell alkalmazni (ezek is levezethetőek a Maxwell-egyenletek inegrális alakjaiből határátmenetekkel), nevezetesen:
egész számú többszöröse, akkor a görbe egy egyenes párt alkot, ekkor beszélünk lineáris polarizációról. Ha a szög 90-foknak páratlan többszöröse, és a két méretszorzó egyezik, akkor cirkuláris a polarizáció. Egyéb esetben általános, elliptikus polarizációról beszélünk. Az elektromágneses hullám polarizációja befolyásolja a kölcsönhatását a határfelületekkel, és az optikailag aktív közegekkel. A közegben terjedő változásokat a közegbeli Maxwell-egyenletekből számolhatjuk, a határfelületeken a határfelületi törvényeket kell alkalmazni (ezek is levezethetőek a Maxwell-egyenletek inegrális alakjaiből határátmenetekkel), nevezetesen:
- Az elektromos térerősség érintő irányú komponense változatlanul megy át a határfelületen,
- A mágneses indukció normális irányú komponense változatlanul megy át a határon, továbbá
- H érintő irányú komponense és
- D normális komponense is.
A polarizációs jelenségekről röviden illik tudni, hogy különböző anyagok rendelkezhetnek optikai aktivitással, ezáltal befolyásolhatják a polarizáció szögét, esetleg a különböző polarizációkra eltérő törésmutatókat mutatnak, stb.
Érdemes még megjegyezni a Faraday-effektust, ahol mágneses tér által lehet az anyag optikai aktivitását befolyásolni.
Kristályoptika
Amint látható a hullámoptika igen alapvető kapcsolatban van az anyagiegyeneltekkel, azonban ezek az összefüggések csak első közelítésben tekinthetőek lineárisnak. Az anyagi egyenletek második közelítésben 3x3-as szimmetrikus tenzorokkal jellemezhető összefüggést tartalmaznak, amelyek jelentősen megváltoztatják a diszperziós relációt: irányfüggővé teszik azt, azáltal anizotróp anyagokhoz jutunk, amelyekben a terjedési sebesség függ az iránytól. Ezek a mindennapokban például a kettőstörő anyagokban figyelhetőek meg.
Törés és visszaverődés
A fentiekből levezethető a jólismert Snellius-Descartes törvény, amely a különböző törésmutatójú közegek határán bekövetkező törést és visszaverődést írja le. A fenti határfeltételeket rójuk ki a felület teljes részére minden időpillanatban. Ha a beérkező hullám 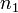 törésmutatójú közegből, a normálishoz mért
törésmutatójú közegből, a normálishoz mért 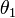 szöggel érkezik, és a megtört sugár közegében
szöggel érkezik, és a megtört sugár közegében 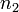 a törésmutató, akkor a
a törésmutató, akkor a 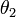 az ellentett normálishoz mért szögre fennáll:
az ellentett normálishoz mért szögre fennáll:
A viszavert hullám szöge teljesen szokásos módon megegyezik a visszaverttel.
Fresnel-formulák
A fenti egyenletek csak a terjedési irányokat adják meg. Ha az amplitúdokra is kíváncsiak vagyunk, akkor szükségünk van a Freshnel-formulákra, továbbá a beérkező síkhullámot fel kell bontani a kétirányú transzverz polarizációkra. Ezekből meghatározhatók a visszavert és a megtört amplitúdók, amelyek összege ki kell hogy adja a beérkező hullámét. A formulákat lásd itt.
Interferencia
Két síkhullám találkozásakor a térmennyiségek tekintetében semmi különleges nem történik, hiszen a Maxwell-egyenletek lineárisak, így mindkét hullám létrehozza saját hatását, és ezek összegződnek. Azonban a megfgyelhető intenzitások (és energiák) az amplitúdók négyzetével arányosak, és a négyzetek nem adódnak össze. A hullámok összegének négyzetremelésekor marad egy vegyes tag, ami a síkhullámok fáziskülönbéségtől függ. Attól függően, hogy a hullámok milyen fázisban találkoznak, erősíthetik, vagy gyengíthetik egymást, azaz a megfigyelt intenzitás nagyban változhat. Ezt a jelenséget nevezzük interferenciának. Ahhoz hogy tartós interferenciát tudjunk megfigyelni, a következő feltételeknek kell teljesülniük:
- Azonos frekvenciájú legyen a két hullám. Másképp a vegyes tag időátlaga (két koszinusz szorzatának időintegrálja) közel nulla lesz.
- Ne legyen merőleges a polarizáció, azaz minnél hasonlóbb polarizációjú hullámokat ejtsünk egybe.
- A fényforrásokból kibocsájtott hullámfronok fáziskülönbsége időben állandó kell legyen. Random fázistényező esetén az interferenciális hatások kiátlagolódnak, és nem látunk interferenciát.
Ez utóbbi feltételt koherencia feltételnek is nevezhetjük. Vagy lézerekkel, vagy egy koherens hullámvonulat kettéosztásával, majd egyesítésével teljesíthető.
Diffrakció
A Maxwell-egyenletek megoldásával elvileg tetszőleges elrendezésben kitudjuk számolni a hullámok terjedését, azonban ez már igen egyszerű helyzetkeben is elbonyolodik. A diffrakció a fény akadályokkal való kölcsönhatását írja le, azonban itt már közelítésekkel élünk.
Huygens-Fresnel-elv
A kísérleti eredmények igen jól leírhatóak a következő állítás segítségével:
- A fény akadállyal való találkozása során a hullám az akadály helyén zérus amplitúdót vesz fel, a határfelület minden pontja pedig gömbforrásként tekintendő. A tovahaladó hullám a sok gömbhullám szuperpozíciója.
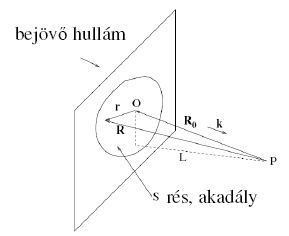
Az akadályokról tovahaldó hullámfrontot így az egyes gömbforrások integráljaként lehet kezelni, az ezt leíró skaláris elmélet alapképlete:
Itt U(p) a p-pontbeli amplitudó, U(r) a bejövő hullám a résnél.
ennek bizonyos gyakori közelítéseit érdemes ismerni:
- A réshez közel, vagy tetszőleges távolságban de szemből nézve Freshnel közelítést kell használni:
- A réstől távol, és ferdén nézve Fraunhofer közelítést kell használni:
Érdemes tudni a féltér elhajlási képét, és a kerek rés képét, az itt fellépő Poisson foltot (köralakú kitakarás mögött fényes folt) az elsőhöz, a másodikhoz a vékony rés, és a körnél fellépő Airy-korongot. Képek az optika jegyzet 3-as pdf-jében.
Fourier-optika
Belátható, hogy amikor elhajlási képeket számolunk, akkor a fellépő integrál a síkhullámból örökölt expinenciálissal együtt voltaképpen a diffraktív felület Fourier-transzformációját írja le. Ezek után lényegileg a kétdimenziós Fourier transzformáció apparátusával tárgyalható tetszőleges elrendezés elhajlási képe, ami nagyban megkönnyíti és egységesíti a tárgyalásmódot, különösen szabályos, illetve rácsszerkezetű diffraktív felületek esetén.
Nemlineáris optika alapjai
Nemlineáris, elektrooptika
A közeg polarizációja továbbá nem csak az irányfüggésben lehet bonyolult, hanem a dielektromos állandó, és ezen keresztül a törésmutató térerősségfüggésében. Ez azt jelenti, hogy kellően nagy energiájú sugár (lézerfény) megváltoztatja a közeget maga körül, és ez utána visszahat a saját terjedésére. Ezt a terjedést és visszahatást a nemlineáris optika tárgyalja, itt a szuszceptibilitáshoz magasabb rendű korrekciókat is figyelembe kell venni.
Ha a sugár energiája kicsi, de mi kapcsolunk külső erős sztatikus teret a közegre, akkor ugyanígy befolyásolhatjuk a terjedést, ez az elektrooptika. A térerősség első hatványával történő megváltozás a Pockels effektus, a négyzetével arányos a Kerr-effektus.
További effektusok a Cserti József Optika 10. jegyzetében találhatóak.
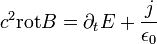
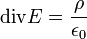
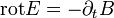
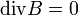
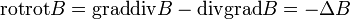
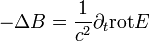
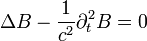
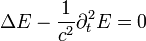
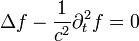
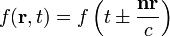
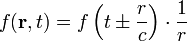
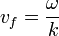
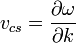
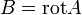
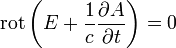
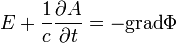

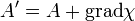
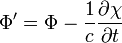
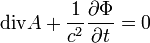
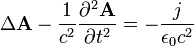
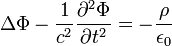
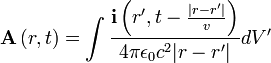
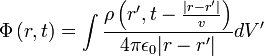
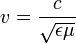
![\left(\Delta - \frac{\partial^2}{\partial z^2} + \mu\epsilon\omega^2 - k^2 \right) \left[ \mathbf{E}, \mathbf{B} \right] = 0](/images/math/5/8/c/58c0533881306d6384f8abfdda69369a.png)