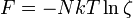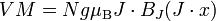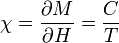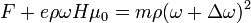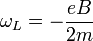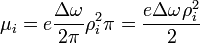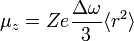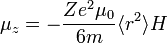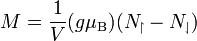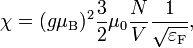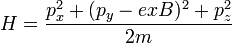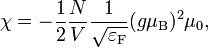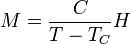„Kölcsönható rendszerek, mágneses anyagok” változatai közötti eltérés
(→Pauli-szuszceptibilitás) |
(→Landau diamágnesség) |
||
| 305. sor: | 305. sor: | ||
ahol az utolsó tényezőben a Fermi-energia szerepel. | ahol az utolsó tényezőben a Fermi-energia szerepel. | ||
| − | ===Landau diamágnesség=== | + | ===Landau-diamágnesség=== |
A diamágnesség ezen másik modellje már kvantummechanikai megfontolásokon alapul. Az alapötlet szerint a szabad elektornok a mágneses térben körben mozognak, amei megint mágneses teret kelt, és ez gyengíti le a külső teret. Kiindulásként a szabad elektorn mágneses térbeli Hamilton-operátora szolgál: | A diamágnesség ezen másik modellje már kvantummechanikai megfontolásokon alapul. Az alapötlet szerint a szabad elektornok a mágneses térben körben mozognak, amei megint mágneses teret kelt, és ez gyengíti le a külső teret. Kiindulásként a szabad elektorn mágneses térbeli Hamilton-operátora szolgál: | ||
| − | :<math>H = \frac{p_x^2 + (p_y - | + | :<math>H = \frac{p_x^2 + (p_y - exB)^2 + p_z^2}{2m}</math> |
| − | Azért kell kvantumosan számolni, mert klasszikusan a mágneses tér kitranszformálható, mi pedig éppen az aszerinti függést | + | Azért kell kvantumosan számolni, mert klasszikusan a mágneses tér kitranszformálható, mi pedig éppen az aszerinti függést keressük. A rendszert jellemző hullámfüggvényt felbontjuk egy <math>y</math>-tól és <math>z</math>-től, valamint egy <math>x</math>-től függő rész szorzatára, és vizsgáljuk a Schrödinger-egyenlet megoldását, amelyben felismerjük a harmonikus oszcillátor energiáját. Az energiát <math>y</math> és <math>z</math> szerint azonban még ki kell számolni, ezt az állapotsűrűség fölhasználásával tesszük. A mágnesezettséget az energia tér szerinti deriváltjából határozzuk meg, ebből pedig a szuszceptibilitás kapható meg: |
| − | :<math>\chi = -\frac{1}{2} \frac{N}{V} \frac{1}{\ | + | :<math>\chi = -\frac{1}{2} \frac{N}{V} \frac{1}{\sqrt{\varepsilon_{\text{F}}}} (g \mu_{\text{B}})^2 \mu_0,</math> |
amely éppen a Pauli-szuszceptibilitás -1/3-a. | amely éppen a Pauli-szuszceptibilitás -1/3-a. | ||
A lap 2011. június 15., 11:59-kori változata
Tartalomjegyzék
Ritka gázok állapotegyenlete
Tekintsük a következő Hamilton-operátorral jellemezhető rendszert:
Az első tag a részecskék mozgásienergiája és belső gerjesztettsége, második a kölcsönhatást jellemző potenciál. Analitikusan a következők számolhatók ki ebből:
- ritka gázok: gyenge a kölcsönhatás, és kicsi a járuléka,
- szilárd és amorf anyagok: erős a kölcsönhatás, de kicsi a hőmérséklet, ezért a részecskék a potenciál minimuma körül rezegnek.
Minket most a ritka gázok állapotegyenlete érdekel. Írjuk fel az állapotösszeget:
ahol az impulzust kiintegráltuk:
Azonban a potenciált nem tudjuk kiintegrálni ilyen általánosan, arról valamilyen modellt kell alkotni. Feltesszük a következőket:
- A kölcsönhatás párkölcsönhatás, mégpedig úgy, hogy csak a két kölcsönható részecske távolságának abszolut értékétől függ.
- Valamilyen modell függényt tételezünk fel a párkölcsönhatásra. Ez lehet például Lenard-Jones, vagy a merev gömb: egy bizonyos
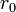 közelségen belül végtelenül nagy a potenciál, azaz ennél közelebb nem kerülhetnek egymáshoz a részecskék. A mostani levezetés általános, az utolsó I integrál tartalmazza ezt expliciten.
közelségen belül végtelenül nagy a potenciál, azaz ennél közelebb nem kerülhetnek egymáshoz a részecskék. A mostani levezetés általános, az utolsó I integrál tartalmazza ezt expliciten.
Amit tehát ki szeretnénk számolni:
Tekintsük egy pillanatra az átlagos potenciális energiát itt, és a kanonikus tárgyalásban a belső energiát:
Az első egyenletben szándékosan vittük be az állapotösszeget, ugyanis az így kapott tört a koordinátakonfiguráció valószínűségét jelenti, analógiában a kanonikus modellbeli mikroállapot valószínűséggel. A kanonikus tárgyalásban azonban U-t feltudtuk írni z deriváltjaként, és az analógiát felhasználva itt is megtesszük 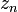 -re:
-re:
Ez utóbbit felintegrálva kapjuk:
c-ről belátható a határokon felvett értékek alapján, hogy 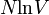 .
.
Írjuk fel az átlagos potenciális energiát, mint párkölcsönhatások összegét is:
Ezt szeretnénk egyenlővé tenni az előbb megfogalmazott valószínűségi integrállal, azonban annyit már elértünk, hogy a részecskék már csak a valószínűségben vannak csatolva. A továbbiakban felírjuk a nevezőt is integrál alakban, áttérünk a helykoordináták különbségére (r), mint változóra, ekkor az integrálok fele elvégezhető, ami térfogatot ad és kiesik. A maradékot felírjuk, mint 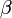 szerinti deriváltat. Ez már igen egyszerű alakú:
szerinti deriváltat. Ez már igen egyszerű alakú:
Ehhez kihasználtuk azt a feltevést, hogy csak kettős ütközések vannak, a többrészecskék ütközéseket elhanyagoltuk. A továbbiakban feltesszük, hogy az 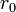 , mint a részecskék méretét jellemző paraméter sokkal kisebb mint a térfogatot jellemző méretek. Az integrált exponenciális függgvény szinte mindenütt 1 (mert az argumentuma 0), kivéve
, mint a részecskék méretét jellemző paraméter sokkal kisebb mint a térfogatot jellemző méretek. Az integrált exponenciális függgvény szinte mindenütt 1 (mert az argumentuma 0), kivéve 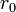 közelében, ezért becsempészünk nullát, mint +1 -1. Az így kapott exponenciális integrál (I) csak
közelében, ezért becsempészünk nullát, mint +1 -1. Az így kapott exponenciális integrál (I) csak 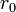 közelében jelentős, ezért kicsit átírva sorbafejthető. Eredményül azt kapjuk, hogy:
közelében jelentős, ezért kicsit átírva sorbafejthető. Eredményül azt kapjuk, hogy:
Ezt behelyettesíthetjük a párkölcsönhatások felösszegzésébe, ezután pedig az egész átlagos potenciális energiát beírjuk a kanonikus analógiából kapott 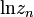 képletbe, és elvégezzük az integrált:
képletbe, és elvégezzük az integrált:
Itt már látszik, hogy az első tag a klasszikus ideális gázhoz tartozik, a másodikaz új, korrekciós tag. Az állapotegyenletet a 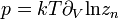 összefüggésből számolhatjuk:
összefüggésből számolhatjuk:
Az eljárás tovább folyatatható, egyre több korrekció adható az ideális gáz egyenletéhez, további integrálos együtthatók jelennek meg, amelyek N/V egyre magasabb hatványaival skáláznak.
Viriál sorfejtés
A fentebb levezetett nyomásképlet általános alakban az úgynevezett viriál sorfejtés, amelyet a nyomásra vezethetünk le:
A fenti esetben csak a kétrészecske kölcsönhatásokat vettük figyelembe, a további kölcsönhatások figyelembevétele és a megfelelő viriál-együtthatók integráljainak felírása kombinatorikai feladattá növi ki magát. Az egyes viriál együtthatók továbbá mindig függnek a hőmérséklettől is. További információ itt.
Van der Waals gázok
A fenti ritka gázokra adott levezetéshez igen hasonló módon levezethető a Van der Waals féle valós gázok modelljének állapotegyenlete. Induljunk ki ideális gázból, amelyet N darab megkülönböztethetetlen részecske alkot. Ennek a Hamiltonja:
Az ennek megfelelő egyrészecske állapotösszeg:
Itt elvégeztünk két integrált, a helyszerinti egyszerűen a térfogatot adta, az impulzus szerintit pedig Guass-intergál segítségével tudtuk elvégezni. Bevezettük továbbá a termikus hullámhossz jelölését is, ami megközelítőleg a részecskék átlagos de Brogile hullámhossza adott hőmérsékleten, ideális gázban:
A korábbiakból a teljes állapotösszeg:
Most továbblépünk az ideálisgázokról, és feltételezzük, hogy a részecskék között a következő párpotenciál van:
r két részecske távolságát jelöli, d azt a távolságot ahol két részecske éppen érinti egymást. A potenciál definíciója miatt ennél közelebb nem lehetnek egymáshoz. Ezt egyben azt is jelenti, hogy a teljes térfogat nem megengedett a részecskék számára, abból le kell vonni a potenciál által tiltott részt:
Azért kellett egy további kettes faktorral leosztani, mert különben a kizárt térfogatot duplán számoltuk volna. Továbbá bevezetjük a részecskék közötti átlagospotenciált, amit a fentiek felhasználásával egy homogén részecskesűrűségre:
Ami a szokásos dr vastagságú gömbfelület darabok felösszegzése. Elvégezve az integrált bevezethetünk két konstanst, az egyiket azonosíthatjuk is a fentebbi fajlagos kirekesztett térfogattal (b):
A potenciálhoz szintén egy energia tartozik, amelyben az eloszlás Boltzmann-eloszlás, azért ezt is bevezetjük, azonban a túlszámlálás elkerülésére itt is bevezetünk egy 1/2-es faktort. A módosított térfogatot és a potenciált beírva az állapotösszegbe:
Ezekután érdemes az állapotösszeg logaritmusát venni, amelyből a nyomás meghatározható, a ritkagázokhoz hasonlóan:
Algebrai átalakítások után megkapjuk a Van der Waals gázok állapotegyenletét:
Ising-modell
Az Ising-modell figyelembe veszi a szomszédos spinek közötti kölcsönhatást, egy (ferromágneses) rendszer energiája így:
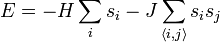
A második összegzés csak azokra az 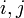 párokra értendő, amik elsőszomszédok. Az egyszerűség kedvéért tegyük fel, hogy csak két állapot lehetséges, tehát az atomok spinje:
párokra értendő, amik elsőszomszédok. Az egyszerűség kedvéért tegyük fel, hogy csak két állapot lehetséges, tehát az atomok spinje: 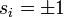 . Az első tag a
. Az első tag a 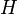 nagyságú külső mágneses térrel vett kölcsönhatás, a második tag a szomszédos spinek közötti kölcsönhatás járuléka. Ferromágnesnél az a kedvező energiájú helyzet, ha a szomszédos spinek ugyanabba az irányba mutatnak, így a
nagyságú külső mágneses térrel vett kölcsönhatás, a második tag a szomszédos spinek közötti kölcsönhatás járuléka. Ferromágnesnél az a kedvező energiájú helyzet, ha a szomszédos spinek ugyanabba az irányba mutatnak, így a 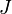 együttható pozitív.
együttható pozitív.
Természetesen a valóságban a távolabbi spinek között is lehet kölcsönhatás, az Ising-modellnek azonban jelentős előnye, hogy 1 és 2 dimenzióban egzaktul megoldható.
Az Ising-modell megoldása 1 dimenzióban(*)
Az egyszerűség kedvéért periódikus határfeltételekkel számolunk ( vagyis 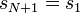 , de ez nem változtatja meg jelentősen a végeredményt), így a modellt úgy lehet elképzelni, hogy a
, de ez nem változtatja meg jelentősen a végeredményt), így a modellt úgy lehet elképzelni, hogy a 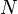 spin egy gyűrű mentén helyezkedik el. A rendszer energiája:
spin egy gyűrű mentén helyezkedik el. A rendszer energiája:
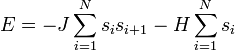
A termodinamikai mennyiségek meghatározásához írjuk fel az állapotösszeget:
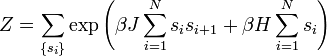
Az összegzés az összes elképzelhető 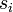 sorozatra értendő. Az exponenciálist szorzattá lehet bontani, és a szorzást a sorozatokra vett összegzéssel fel lehet cserélni:
sorozatra értendő. Az exponenciálist szorzattá lehet bontani, és a szorzást a sorozatokra vett összegzéssel fel lehet cserélni:
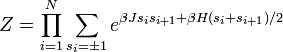
Vezessük be két spin között a következő transzfermátrixot:
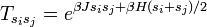
Mivel 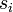 és
és 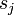 értéke is
értéke is 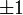 lehet,
lehet, 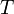 egy
egy 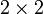 mátrix lesz:
mátrix lesz:
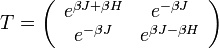
Ekkor az állapotösszeg felírható a transzfermátrixszal:
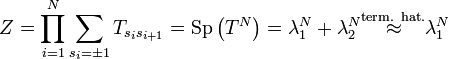
Az állapotösszeg a mátrix 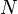 -edik hatványának a spurja, ami kifejezhető a
-edik hatványának a spurja, ami kifejezhető a 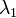 és
és 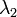 sajátértékek hatványával. Mivel
sajátértékek hatványával. Mivel 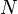 nagyon nagy, ezért a kisebb sajátérték hatványa elhanyagolható a nagyobbhoz képest a termodinamikai határesetben. A transzfermátrix sajátértékei:
nagyon nagy, ezért a kisebb sajátérték hatványa elhanyagolható a nagyobbhoz képest a termodinamikai határesetben. A transzfermátrix sajátértékei:
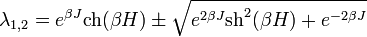
Ha nincs külső tér 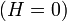 , az állapotösszeg:
, az állapotösszeg: 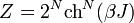 . A mágnesezettség külső tér esetén:
. A mágnesezettség külső tér esetén:
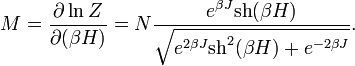
Ha 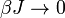 , tehát függetlenek a spinek, akkor
, tehát függetlenek a spinek, akkor 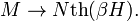 A szuszceptibilitás:
A szuszceptibilitás:
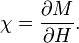
A korrelációs függvény:
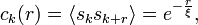 ahol
ahol
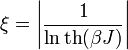 a korrelációs hossz. Ez tekinthető az átlagos doménméretnek.
a korrelációs hossz. Ez tekinthető az átlagos doménméretnek.
Antiferromágneses Ising 1 dimenzióban(*)
A Hamilton-függvény abban különbözik a ferromágneses esettől, hogy pozitív a 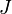 együttható, azaz fordítva szeretnek állni a szomszédos spinek:
együttható, azaz fordítva szeretnek állni a szomszédos spinek:
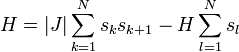 .
.
Ugyanazt kapjuk, mint az előző esetben, csak 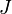 helyére mindenhol
helyére mindenhol 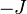 -t kell írni a képletekben. A korrelációs függvény változik jelentősen, mert oszcillálni fog az értéke:
-t kell írni a képletekben. A korrelációs függvény változik jelentősen, mert oszcillálni fog az értéke:
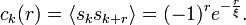
Érdekes módon itt már egydimenzióban megjelenik a fázisátmenet. Alapállapotban az összes spin váltakozó irányban áll, így a külső tér energiajáruléka eltűnik, hiszen 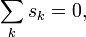 valamint
valamint 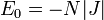 . Azonban, ferromágneses beállás mellett létezik egy olyan külső tér, ahol az energia éppen akkora, mint az antiferromágneses alapállapotban:
. Azonban, ferromágneses beállás mellett létezik egy olyan külső tér, ahol az energia éppen akkora, mint az antiferromágneses alapállapotban:
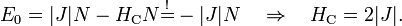
Ezen külső térnél teljesen mindegy, hogyan állnak a spinek, mindig ugyanennyi lesz az energiájuk, tehát az entrópia a végtelenhez tart termodinamikai határesetben, nulla kelvinen.
Az Ising-modell átlagtérelmélete 2 dimenzióban(**)
Az Ising-modell 2 dimenzióban is megoldható egzaktul, de ez nagyon bonyolult, ezért itt egy átlagtérelméleti közelítést mutatunk be. Az energia kifejezésében a spinváltozókhoz adjuk hozzá és vonjuk is le a várható értéküket, jelölje ezt 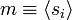 :
:
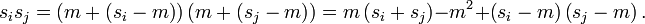
Az utolsó tag az átlagtól való eltérések szorzata, amit a továbbiakban elhanyagolunk (másodrendűen kicsiny), így nem lesz két spin szorzatát tartalmazó tagunk, a rendszer úgy kezelhető, mint egy szabad spinrendszer, amire az átlagos térnek megfelelő külső tér hat. Az energia így felírva:

Itt 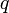 az elsőszomszédok száma, amit koordinációs számnak hívnak. Az állapotösszeg:
az elsőszomszédok száma, amit koordinációs számnak hívnak. Az állapotösszeg:
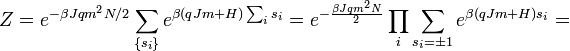
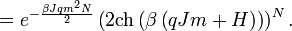
Ebből kiszámítható a mágnesezettség várható értéke:
![m = \langle s_i \rangle = \operatorname{th} \left [ \beta \left ( q J m + H \right ) \right ].](/images/math/e/d/6/ed6b04b7261366b8044ff7689557e67a.png)
A számolás alatt végig felhasználtunk egy 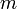 paramétert, mint átlagos mágnesezettséget, de ennek az értéke nem tetszőleges, hanem olyan, hogy a fenti egyenletet kielégíti. Az egyenletet érdemes grafikusan megoldani. Mindkét oldalt
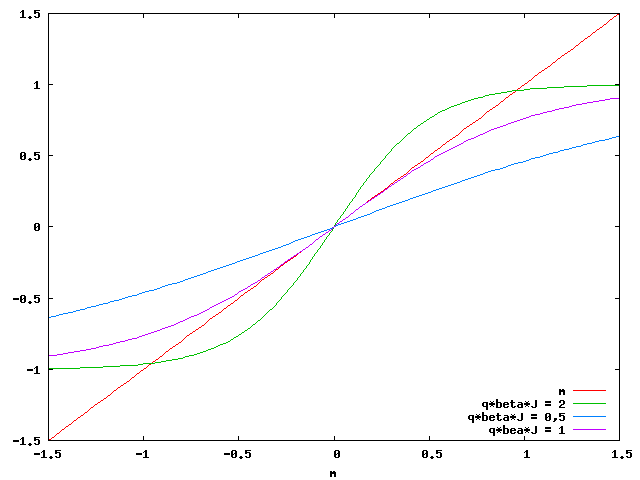
paramétert, mint átlagos mágnesezettséget, de ennek az értéke nem tetszőleges, hanem olyan, hogy a fenti egyenletet kielégíti. Az egyenletet érdemes grafikusan megoldani. Mindkét oldalt 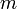 függvényében ábrázolva, a baloldal egy
függvényében ábrázolva, a baloldal egy 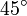 meredekségű egyenes, a jobb oldal egy tangens hiperbolikusz függvény. A két görbe metszéspontjai az egyenlet megoldásai.
meredekségű egyenes, a jobb oldal egy tangens hiperbolikusz függvény. A két görbe metszéspontjai az egyenlet megoldásai.
A tangensfüggvény meredeksége viszont függ a hőmérséklettől is, így egy kritikus hőmérséklet felett csak egy, alatta viszont három megoldás van. A kritikus hőmérséklet alatt az anyag viselkedése ferromágneses, felette paramágneses, a kritikus hőmérsékleten másodrendű fázisátalakulás játszódik le. Ha a külső tér 0, akkor az egyik megoldás mindig az origóban van, a másik két megoldás pedig szimmetrikusan helyezkedik el. Ha a külső tér nem 0, akkor a megoldások eltolódnak, elég nagy tér melett már a ferromágneses fázisban is csak egy megoldás lesz.
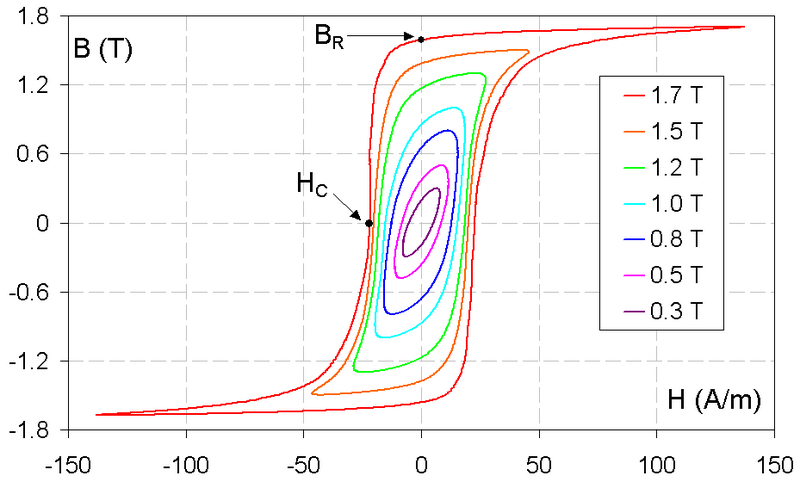
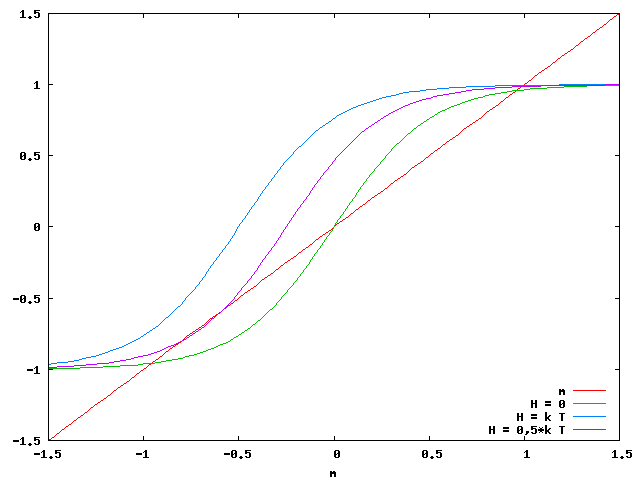
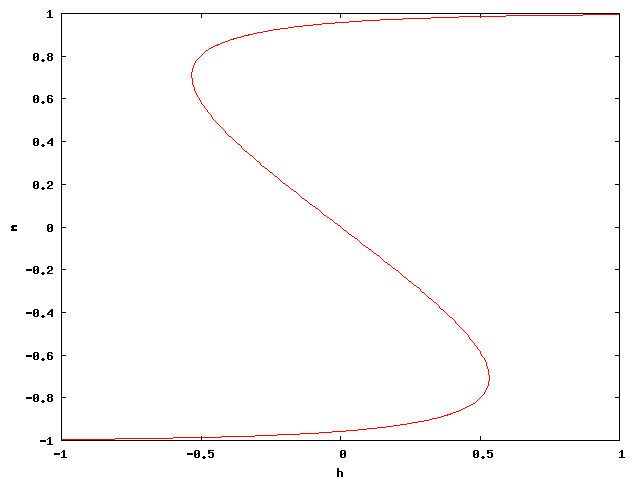
A mágnesezettséget a külső tér függvényében ábrázolva (az alábbi ábra 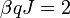 paraméter mellett készült) S alakú görbét kapunk, egy kritikus külső tér érték felett már csak egy megoldás létezik, alatta három. A három megoldás közül azonban a középső instabil (a megoldások a szabadenergia szélsőértékeihez tartoznak, a két szélső megoldás minimum, a középső maximum), így a külső teret mondjuk egy magas értékről egyre csökkentve a mágnesezettség a felső görbén marad, majd a visszafordulási pontot elérve leugrik az alsó ágra. A külső teret ismét növelve a mágnesezettség az alsó ág mentén haladva növekszik, majd a felső visszafordulási pontot elérve visszaugrik a felső ágra. A mágneses teret a közbülső részben hagyva előfordulhat, hogy a rendszer a termikus fluktuációk hatására átugrik az egyik helyről a másikra. Azokat a pontokat, ahol a mágnesezettség visszafordul, spinodális pontoknak nevezik. Ez a viselkedés a valódi ferromágneses anyagokban található hiszterézishez hasonló. Egy valódi anyag azonban sok doménből áll, amik kiolthatják egymás hatását, így be lehet menni vele a 0 mágnesezettség környezetébe is. Természetesen ez csak egy közelítő leírás, ami csak a viselkedés jellegét adja vissza, így a ferromágneses anyagok hiszterézise a részletekben eltér ettől.
paraméter mellett készült) S alakú görbét kapunk, egy kritikus külső tér érték felett már csak egy megoldás létezik, alatta három. A három megoldás közül azonban a középső instabil (a megoldások a szabadenergia szélsőértékeihez tartoznak, a két szélső megoldás minimum, a középső maximum), így a külső teret mondjuk egy magas értékről egyre csökkentve a mágnesezettség a felső görbén marad, majd a visszafordulási pontot elérve leugrik az alsó ágra. A külső teret ismét növelve a mágnesezettség az alsó ág mentén haladva növekszik, majd a felső visszafordulási pontot elérve visszaugrik a felső ágra. A mágneses teret a közbülső részben hagyva előfordulhat, hogy a rendszer a termikus fluktuációk hatására átugrik az egyik helyről a másikra. Azokat a pontokat, ahol a mágnesezettség visszafordul, spinodális pontoknak nevezik. Ez a viselkedés a valódi ferromágneses anyagokban található hiszterézishez hasonló. Egy valódi anyag azonban sok doménből áll, amik kiolthatják egymás hatását, így be lehet menni vele a 0 mágnesezettség környezetébe is. Természetesen ez csak egy közelítő leírás, ami csak a viselkedés jellegét adja vissza, így a ferromágneses anyagok hiszterézise a részletekben eltér ettől.
Két dimenzió fölött következik be fázisátalakulás: egy adott hőmérséklet fölött ferromágnesesből átvált paramágnesessé az anyag. A fázisátalakulás hőmérsékletét az határozza meg, hogy ott a tangens hiperbolikusz függvény meredeksége az origóban (a biztos metszéspontban) éppen 1, így még csak egy metszéspont létezik.
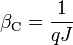
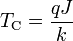
A mágnesezettség a külső tér 1/3-ik hatványával arányosan indul: 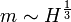 , a kritikus pont körül pedig a hőmérséklet gyökével változik:
, a kritikus pont körül pedig a hőmérséklet gyökével változik: 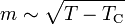 . Érdekes, hogy két dimenzióban éppen a kritikus pont körül használhatatlan az átlagtérelmélet, mert a fluktuációk makroszkopikussá növekednek, a szuszceptibilitás és az átlagos doménméret a végtelenhez tart.
. Érdekes, hogy két dimenzióban éppen a kritikus pont körül használhatatlan az átlagtérelmélet, mert a fluktuációk makroszkopikussá növekednek, a szuszceptibilitás és az átlagos doménméret a végtelenhez tart.
Mágneses anyagok típusai
A mágnesség tárgyalásánál előbukkantak a következő mennyiségek: Mágneses térerősség (H), mágneses indukció vektor (B), mágnesezettség (M). Bevezettük a mágneses szuszceptibilitást, mint anyagi jellemzőt és arányossági tényezőt:
Azaz a mágneses szuszceptibilitás a mágnesezettség és a mágneses térerősség közötti kapcsolat. A szuszceptibilitás lehet pozitív és negatív is, azaz külső mágneses térbe helyezve az anyagot, az vagy erősíti azt, csak csökkenti (a mágnes vonzza, vagy taszítja őket). Utóbbi esetben az anyag diamágneses, az előbbi esetben több mechanizmust különböztetünk meg. A diamágnesség okozói a belső lezárt elektronhéjakon levő elektronok, amelyek a megváltozással szemben hatnak a mágneses momentumuk térrel szembe állításával.
Ferro-, ferri-, és antiferromágneses anyagok
Paramágnességről beszélünk, ha a vonzó, térerősítő hatás csak a külső mágneses tér jelenlétekor érezhető (ez a tér rendezi egyirányba a momentumokat, eltávolításával azok újra rendezetlenné válnak, és zérusra átlagolódik a hatásuk). A diamágnességgel együtt gyengének tekinthetőek. A ferro-, ferri- és antiferromágneses anyagokban a mágnesesség forrásául szolgáló atomi momentumok eleve rendezetten állnak, a különbség csak az irányban és a méretben van. Ha az atomi rendben azonos méretű és egyirányba álló momentumok vesznek részt, akkor az anyag ferromágneses, így ez állandómágneses jelleget mutat. Ha egymással ellentétesek, és kioltják egymást, akkor antiferromágneses az anyag, ha pedig ellentétes, de különböző nagyságúak a momentumok, akkor ferrimágneses az anyag.
A szilárdtestfizika több elméletet is kidolgozott ezen jelenségek mikroszkopikus magyarázatára.
Domének
A ferromágneses anyagoknál a domének nagy, makroszkopikus méretű azonos beállású területek. Kialakulásuk oka egyszerűen érthető: a momentumoknak kedvező, ha azonos irányba állnak be, azonban amíg a hőmozgás rendezetlenné tudja tenni a rendszert, ez nem érvényesül. Ahogy hűtjük lefelé, egy kritikus pontnál a momentumok beállása erősebb lesz a hőmozgás karakterisztikus energiájánál, és fázisátmenet következik be, a kialakult kis azonos beállású helyek hirtelen makroszkópikus méretűvé tudnak válni, hiszen egymást állítják be a rendezetlen állapotból, ugyanakkor egy másik irányba rendeződött részt nem tudnak megfordítani. Ahol a különböző irányítottságú részek összeérnek, ott lesznek a fázishatárok, vagy doménfalak az anyagban. Külső erős térrel beállítható az egész anyagban az orientáció egyirányúvá, így maximális térerősség nyerhető. Kis térerősségeknél az energetikailag kedvező mágnesezettségű domének "meghíznak" az ellenkező beállásúak rovására, doménfalmozgással történik az átmágneseződés. Nagy terek viszont képesek egész doméneket egyszerre átforgatni. A legtöbb ferromágneses anyagnál számít, hogy melyik kristálytani irányban mágnesezzük föl az anyagot, vannak könnyű és nehéz irányok. A kettő közötti átfordításhoz szükséges a mágneses anizotrópia-energia. Általában egy kristályszemcse több doménre hasad föl, a domének mérete mikrométer alatt van.
Atomi paramágnesség
Másnéven lokalizált parmágnesség. Tekintsük az összes impulzusmomentumot (J = L + 2S), ekkor a mágneses momentum a következőképpen írható:
A B külső térben ez a következő energiát jelenti:
Ha feltesszük, hogy B z irányú. akkor a BJ skaláris szorzatot helyettesíthetjük 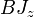 szorzattal. Az energia ismeretében feltudjuk írni az állapotösszeget (
szorzattal. Az energia ismeretében feltudjuk írni az állapotösszeget (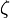 ), azonban mivel az atomok függetlenek, elég egy atom járulékát vizsgálni:
), azonban mivel az atomok függetlenek, elég egy atom járulékát vizsgálni:
Itt csak 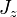 -ben különböznek az állapotok, ezért a kitevő többi részére bevezetjük az
-ben különböznek az állapotok, ezért a kitevő többi részére bevezetjük az 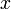 változót, ekkor az összeg egy véges geometriai sorba megy át. A felösszegzés eredménye:
változót, ekkor az összeg egy véges geometriai sorba megy át. A felösszegzés eredménye:
Az egyrészecske-állapotösszeg ismeretében felírható a szabadenergia:
amelyben 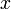 is paraméterként fog szerepelni és a
is paraméterként fog szerepelni és a 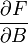 fogja megadni a mágnesezettséget (pontosabban a mágnesezettség-sűrűséget). Az eredményben a bonyolult kotangens hiperbolikuszok helyett bevezettük a Brillouin-függvényt:
fogja megadni a mágnesezettséget (pontosabban a mágnesezettség-sűrűséget). Az eredményben a bonyolult kotangens hiperbolikuszok helyett bevezettük a Brillouin-függvényt:
A Brillouin-függvény alakra hasonló az arkusz tangenshez, de ez a pozitív oldalon 1-hez, negatív oldalon -1-hez tart. Ebből következik, hogy a maradék szorzófaktor a maximális mágnesezettséget adja meg, a függvény alakjából pedig a szaturáció jelensége adódik, ami akkor következik be, amikor az összes mágneses momentumot azonos irányba állítottuk be. Kiszámolhatjuk a függvény 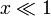 , azaz
, azaz 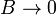 határesetét, amelyet behelyettesítve megkaphatjuk a szuszceptibilitást:
határesetét, amelyet behelyettesítve megkaphatjuk a szuszceptibilitást:
Ahol a számottevő mennyiségű konstanst a 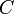 Curie-állandóba vontuk össze. Ez a hőmérséklettel fordítottan arányos szuszceptibilitás függés a Curie-törvény.
Curie-állandóba vontuk össze. Ez a hőmérséklettel fordítottan arányos szuszceptibilitás függés a Curie-törvény.
Atomi diamágnesség
Az atomi diamágnességet szemléletesen úgy magyarázzuk, hogy a külső mágneses tér hatására a keringő elektron pályája megváltozik, és ezáltal a mágneses momentuma is. Keringjen az elektron  sugarú pályán, melynek az atommagon átmenő, térre merőleges vetületének négyzetes középértéke
sugarú pályán, melynek az atommagon átmenő, térre merőleges vetületének négyzetes középértéke 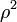 . A keringési frekvencia
. A keringési frekvencia 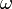 , és legyen a külső mágneses tér H , ekkor a mag vonzó ereje és a Lorentz-erő tart ellent a centrifugális gyorsulással:
, és legyen a külső mágneses tér H , ekkor a mag vonzó ereje és a Lorentz-erő tart ellent a centrifugális gyorsulással:
A négyzetet felbontjuk és a másodrendűen kicsi tagot elhagyjuk. Itt felhasználjuk Larmor tételét, amely azt állítja, hogy egy mágneses térben levő atom elektronjainak mozgása első rendű közelítésben olyan, mintha a tér nem is lenne jelen, csak a körfrekvenciára egy:
precesszió szuperponálódna, ezt feleltetjük meg a fenti kis körfrekvencia-megváltozásnak. A mágnesesmomentum az áram és a felület szorzata, az áramot pedig azzal a definícióval írjuk fel, hogy az áramirányra merőleges felületelemen mennyi töltés halad át egy másodperc alatt. Ezek alapján a mágneses momentum komponensei:
A mágneses momentumhoz csak a térirányához merőleges távolságok járulnak hozzá, az elektron azonban r sugarú pályán kering, ez behoz még egy 3/2-es faktort a távolságnégyzetek között, így a valódi teljes mágneses momentum 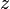 komponense
komponense 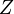 rendszámú atommagra:
rendszámú atommagra:
Behelyettesítve a Larmor-frekvenciát:
Amelyből a szuszceptibilitás már leolvasható, a negatív előjel jelenti a diamágneses hatást. (SI-ben vannak a képletek.)
Pauli-szuszceptibilitás
A Pauli-szuszceptibilitás a parmágnesség egy másik modellje. A modell lényege, hogy a Fermi-energia környékén lévő vezetési elektronok járulnak hozzá az elektronspin-szuszceptibilitáshoz, tehát gyakorlatilag a szabad elektronok paramágnességéről van szó. A hőmérséklettől független, szemben a kötési elektronok paramágneses szuszceptibilitásával, amely hőmérsékletfüggő (Curie-törvény), és kb. két nagyságrenddel nagyobb, mint a Pauli-szuszceptibilitás. Ez az energiaszintek betöltöttségi sűrűségéből számolja ki a felfelé és lefelé álló momentumok mennyiségét. Az állapotsűrűségre a Bethe--Sommerfeld-sorefjtést alkalmazza. Ezek ismeretében ugyanis a mágnesezettség felírható:
N-be a mágneses indukció is bele van olvasztva. Eredményül a szuszceptibilitás:
ahol az utolsó tényezőben a Fermi-energia szerepel.
Landau-diamágnesség
A diamágnesség ezen másik modellje már kvantummechanikai megfontolásokon alapul. Az alapötlet szerint a szabad elektornok a mágneses térben körben mozognak, amei megint mágneses teret kelt, és ez gyengíti le a külső teret. Kiindulásként a szabad elektorn mágneses térbeli Hamilton-operátora szolgál:
Azért kell kvantumosan számolni, mert klasszikusan a mágneses tér kitranszformálható, mi pedig éppen az aszerinti függést keressük. A rendszert jellemző hullámfüggvényt felbontjuk egy 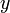 -tól és
-tól és 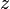 -től, valamint egy
-től, valamint egy 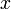 -től függő rész szorzatára, és vizsgáljuk a Schrödinger-egyenlet megoldását, amelyben felismerjük a harmonikus oszcillátor energiáját. Az energiát
-től függő rész szorzatára, és vizsgáljuk a Schrödinger-egyenlet megoldását, amelyben felismerjük a harmonikus oszcillátor energiáját. Az energiát 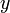 és
és 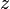 szerint azonban még ki kell számolni, ezt az állapotsűrűség fölhasználásával tesszük. A mágnesezettséget az energia tér szerinti deriváltjából határozzuk meg, ebből pedig a szuszceptibilitás kapható meg:
szerint azonban még ki kell számolni, ezt az állapotsűrűség fölhasználásával tesszük. A mágnesezettséget az energia tér szerinti deriváltjából határozzuk meg, ebből pedig a szuszceptibilitás kapható meg:
amely éppen a Pauli-szuszceptibilitás -1/3-a.
Hiszterézis
A hiszterézis a ferromágneses anyagoknak az átmágnesezéssel szemben mutatott ellenállása. Másképpen megfogalmazva, amikor átakarjuk mágnesezni az anyagot, akkor az valamennyire emlékszik korábbi állapotára, ezért adott irányú és mértékű átmágnesezés után kapott remanens (visszamaradó) mágnesség különböző lehet az anyag előzetes mágnesezettségének függvényében. Legszemléletesebben ezt akkor láthatjuk ha teljesen átmágnesezzük az anyagot egyik, majd másik irányba. A bejárt út különbözik a H-M-síkon. Itt külön névvel illetjük a külső tér megűnésekor hátahagyott mágnesezettséget (ez a remanens mágnesezettség) és az anyag terét éppen kompenzáló kölső térerősséget (koercitív erő).
Curie-Weiss-törvény
A fenti memória effektust Weiss egy belsőtér elmélettel próbálta megmagyarázni. Eszerint a spinek egyirányú beállása okozza a visszamardó mágnesezettségi memóriát, amelyet úgy lehet figyelembe venni, hogy a mágnesezettség a külső téren kívül önmagának is függvénye. Ennek a függésnek a sorfejtéséből levezethető a Curie-Weiss törvény. A domaineknél említettek értelmében kihűlésnél megtörténik a "mágneses kifagyás" afelett azonban a termikus random orientáció dominál. A Curie-Weiss törvény leírja a szuszceptibilitás változását a kifagyási pont felett, a paramágneses hőmérséklet tartományban:
Ez a formula a kifagyás felett érvényes, az átalakulási pontban divergens, ami nyilván nem releváns.
Speciális anyagok
Spinüveg
Egyes speciális anyagokat felmágnesezve azok Curie-törvényt követik, azonban ha elvesszük a külső mágneses teret egy gyors lebomlás után egy remanens mágnesezettséget mutatnak, amely azonban idővel lassan, de tovább bomlik. Ez a viselkedés egyfajta átmenetként fogható fel a ferro és paramágneses anyagok tulajdonságai között. Magyarázata részben a vegyes ferro és antiferromágneses kötések üvegszerű amorf elhelyezkedésében rejlik.
Mágneses ellenállás
Ferrmágneses és nemmágneses rétegek szendvicselésével speciális vezető eszköz készíthető, amelynek ellenállása nagyban függ a külső mágneses tértől: ha kölső mágneses térben van, akkor igen kicsi az ellenállása, ha azonban nicns jelen tér, akkor igen nagy ellenállást mutat. Az effektus mértéke akár több 100% is lehet. A jelenség oka, a különböző spinű elektornokkal szmeben mutatott elelnálás, amely mögött az RKKY magspin és vezetési elektron hiperfinom mágneses csatolása áll.
Szupravezetés
Egyes anyagok igen alcsony hőmérsékletre hűtésekor az elektromos ellenállás egzaktul nullává válik bizonyos hőmérésklet alatt. A jelenséget elektron-elektorn párok (ún. Cooper-párok) létrejöttével sikerült értelmezni, amelyek között a rácsrezgések fononjai tartanak össze. Ilyne párokb jönnek létre egy Bose-Einstein kondenzációhoz hasonló jelenség következtében, mivel az így kialakult párok már bozonként tekinhetőek.
![H = \sum_{i=1}^{N} \left[ \frac{p_i^2}{2m} + \epsilon_i \right] + U(r_1, ..., r_N)](/images/math/f/3/2/f325bf89eda24df40a71b8a1b10ea416.png)
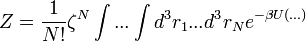
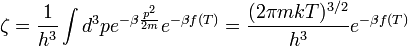
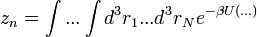
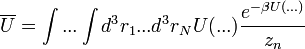

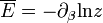
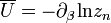
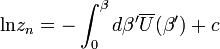
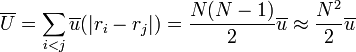
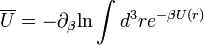
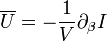
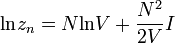
![\frac{p}{kT} = \frac{N}{V}\left[ 1 - \frac{N}{2V}I\right]](/images/math/b/c/0/bc0de49c728c249d36e08c47eca74991.png)
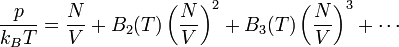
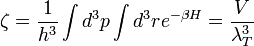
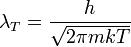
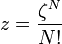
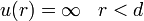
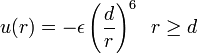
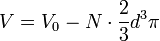
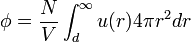
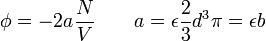
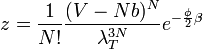
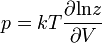
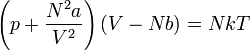
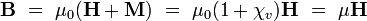
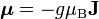
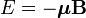
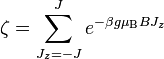
![\zeta=\frac{ \operatorname{sh}\left[ \left( J + \frac{1}{2}\right)x \right]}{\operatorname{sh} \left( \frac{1}{2} x\right)}](/images/math/7/5/d/75de778183762127fe619aed572502c3.png)