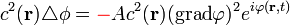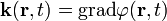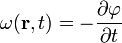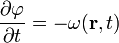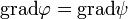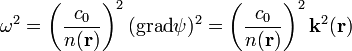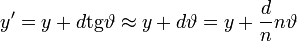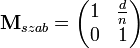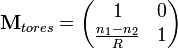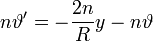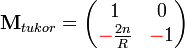„Geometriai optika és alkalmazásai” változatai közötti eltérés
(→Mikroszkóp és felbontóképesség) |
|||
| (Egy közbenső módosítás, amit egy másik szerkesztő végzett, nincs mutatva) | |||
| 119. sor: | 119. sor: | ||
| Hamilton-féle kanonikus egyenletek || <math>\dot{p} = -\frac{\partial H (\mathbf{r},\mathbf{p})}{\partial \mathbf{r}}</math> || || <math>\dot{k} = -\frac{\partial \Omega (\mathbf{r},\mathbf{k})}{\partial \mathbf{r}}</math> || Hamilton-féle sugáregyenletek | | Hamilton-féle kanonikus egyenletek || <math>\dot{p} = -\frac{\partial H (\mathbf{r},\mathbf{p})}{\partial \mathbf{r}}</math> || || <math>\dot{k} = -\frac{\partial \Omega (\mathbf{r},\mathbf{k})}{\partial \mathbf{r}}</math> || Hamilton-féle sugáregyenletek | ||
|- | |- | ||
| − | | | + | | Maupertuis-elv || <math>\delta \int \mathbf{p} dr = 0</math> || || <math>\delta \int \mathbf{k} dr = 0 = \frac{\omega}{c_0} \delta \int n(\mathbf{r}) dl \sim \delta \int n(\mathbf{r}) dl = 0 </math> || Optikai úthossz ~ Fermat-elv |
|} | |} | ||
| 143. sor: | 143. sor: | ||
A mechanikai törésmutató meghatározásánál figyelni kell arra, hogy az analógiát ne a Fermat-elvből levezetett <math>\omega \delta \int \frac{1}{c(\mathbf{r})} dl</math> és ennek mintájára felírt <math>\delta \int \frac{1}{v(\mathbf{r})} dl</math> egyenlet között vegyük, mert <math>c(\mathbf{r})</math> a fázissebesség, a mechanikai analógiában látott <math>\frac{1}{v(\mathbf{r})}</math>-ben a <math>v(\mathbf{r})</math> a csoportsebességnek feleltethető meg, melynek értéke az optikában: <math>\mathbf{v}_g = \frac{\partial \omega}{\partial \mathbf{k}}</math>. | A mechanikai törésmutató meghatározásánál figyelni kell arra, hogy az analógiát ne a Fermat-elvből levezetett <math>\omega \delta \int \frac{1}{c(\mathbf{r})} dl</math> és ennek mintájára felírt <math>\delta \int \frac{1}{v(\mathbf{r})} dl</math> egyenlet között vegyük, mert <math>c(\mathbf{r})</math> a fázissebesség, a mechanikai analógiában látott <math>\frac{1}{v(\mathbf{r})}</math>-ben a <math>v(\mathbf{r})</math> a csoportsebességnek feleltethető meg, melynek értéke az optikában: <math>\mathbf{v}_g = \frac{\partial \omega}{\partial \mathbf{k}}</math>. | ||
| − | A helyes analógia a Fermat-elv és a | + | A helyes analógia a Fermat-elv és a Maupertuis-elv közötti megfeleltetés. Ezt végigszámolva a mechanikában a törésmutató értékére a következőt kapjuk: <math>0 = \delta \int \mathbf{p}(\mathbf{r}) d\mathbf{r} = \delta \int \left| p \right| dl = \delta \int \sqrt{2m(E-V(\mathbf{r}))}dl</math>, mivel <math>E = \frac{\mathbf{p}^2}{2m} - V(\mathbf{r})</math>. |
Ennek nyomán a törésmutató analogonja a mechanikában: <math>n(\mathbf{r}) = \sqrt{E-V(\mathbf{r})}</math>. <math>V(\mathbf{r}) = eU(\mathbf{r})</math> alkalmas megválasztásával elektrosztatikus lencsék/tükrök készíthetőek. | Ennek nyomán a törésmutató analogonja a mechanikában: <math>n(\mathbf{r}) = \sqrt{E-V(\mathbf{r})}</math>. <math>V(\mathbf{r}) = eU(\mathbf{r})</math> alkalmas megválasztásával elektrosztatikus lencsék/tükrök készíthetőek. | ||
| 292. sor: | 292. sor: | ||
===Vékony lencse leképezése=== | ===Vékony lencse leképezése=== | ||
| − | A vékony lencse leképezésének leírásához három mátrixot kell figyelembe vennünk, egyszer a | + | A vékony lencse leképezésének leírásához három mátrixot kell figyelembe vennünk, egyszer a [[tárgytávolságnyi]] szabad terjedés mátrixát, egyszer a törés mátrixát (a fent megismert összefüggés alapján), egyszer pedig a lencsétől a képtávolságig terjedő szabad terjedés mátrixát. Ezeket összeszorzova kapjuk meg a teljes optikai rendszer mátrixát, ami a következőképpen néz ki: |
<math>M = \left( \begin{array}{cc}1 & k\\0 & 1\end{array} \right) \left( \begin{array}{cc}1 & 0\\-\frac{1}{f} & 1\end{array} \right) \left( \begin{array}{cc}1 & t\\0 & 1\end{array} \right) = \left( \begin{array}{cc}1 - \frac{k}{f} & k + t - \frac{kt}{f}\\-\frac{1}{f} & 1 - \frac{t}{f}\end{array} \right)</math> | <math>M = \left( \begin{array}{cc}1 & k\\0 & 1\end{array} \right) \left( \begin{array}{cc}1 & 0\\-\frac{1}{f} & 1\end{array} \right) \left( \begin{array}{cc}1 & t\\0 & 1\end{array} \right) = \left( \begin{array}{cc}1 - \frac{k}{f} & k + t - \frac{kt}{f}\\-\frac{1}{f} & 1 - \frac{t}{f}\end{array} \right)</math> | ||
A lap jelenlegi, 2012. január 10., 16:19-kori változata
Megjegyzés: ez a tétel nagyon erősen követi Cserti József "Optika és Relativitáselmélet" tárgyra készített diáit, lényegében azok kivonata a tétel tematikáját figyelembe véve. Ezekből a diákból is nagyon jól lehet tanulni, megtalálhatóak Cserti József honlapján.[1]
Tartalomjegyzék
Bevezető, fény, fénysugár
A geometriai optika nem foglalkozik a fény hullám, vagy részecske tulajdonságával. Pusztán a fény viselkedését írja le olyan távolság- és időértékeknél, melyek jóval nagyobbak, mint a fény néhány mennyiségi jellemzője.
Alapfeltevései [2]:
- a fény egyenes vonalban terjed, ha homogén közegben halad és semmi sincs az útjában
- közeghatárokon megtörik és/vagy visszaverődik
- visszaverődésnél a beesési és visszaverődési szög megegyezik
- törésnél a beesési és törési szög közötti összefüggést a Snellius-Descartes törvény adja meg:
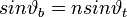 , ahol
, ahol 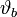 a beesési,
a beesési, 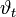 a törési (transzmissziós szög), n egy arányszám, az adott közeg (vákuumhoz viszonyított) törésmutatója.
a törési (transzmissziós szög), n egy arányszám, az adott közeg (vákuumhoz viszonyított) törésmutatója.
- a fénysugarak közt egymásra hatás nem mutatkozik
A Fermat-elv
A Fermat-elv, vagy legrövidebb idő elve azt mondja ki, hogy két pont között a fény az összes lehetséges út közül azt választja, aminek megtételéhez a legrövidebb időtartam szükséges.[3]
Közegben a fény sebessége: 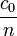 , ahol n a fent említett törésmutató (mely függhet anyagtól, helytől, vagy a fény színétől),
, ahol n a fent említett törésmutató (mely függhet anyagtól, helytől, vagy a fény színétől), 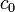 pedig a vákuumbeli fénysebesség, értéke a Maxwell-egyenletek alapján:
pedig a vákuumbeli fénysebesség, értéke a Maxwell-egyenletek alapján:
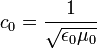 , ahol
, ahol 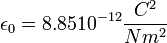 a vákuum dielektromos állandója.
a vákuum dielektromos állandója. 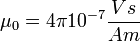 a vákuum permeabilitása. A fentiek alapján:
a vákuum permeabilitása. A fentiek alapján: 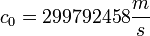 .
.
A Fermat-elv tehát azt mondja ki, hogy a fény két pont között a legrövidebb idő alatt megtehető utat teszi meg. Kicsit pontosabban a fénysugár pályáját sok más szomszédos, csaknem azonos időt igénylő terjedési út közül választja.[4] Ennek kiszámítása a következőképpen történik:
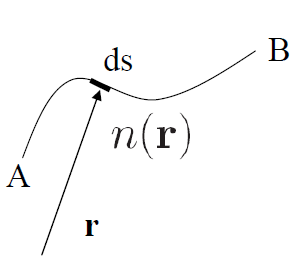
A fenti pályára vett integrálnak (ahol n(r) helyfüggő változó) szélsőértéket kell adnia. 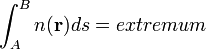 , ahol r a helyvektor[5]. Pl.:
, ahol r a helyvektor[5]. Pl.:
Az eikonál közelítés
| Homogén eset | Inhomogén eset | |
| Hullámegyenlet | 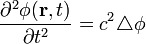 |
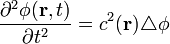
|
| Megoldása | 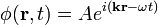 |
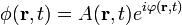
|
Az inhomogén esetben felírt megoldás csak a lassan változó amplitudójú (A), és gyorsan változó fázisú (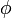 -
- 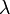 távolságon
távolságon 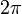 -t változik) síkhullámokra vonatkozik. Lassan változó alatt azt értem, hogy a karakterisztikus hossz
-t változik) síkhullámokra vonatkozik. Lassan változó alatt azt értem, hogy a karakterisztikus hossz 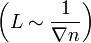 jóval nagyobb, mint a hullámhossz (
jóval nagyobb, mint a hullámhossz (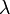 ). Tehát inhomogén esetben, lassan változó amplitudó és gyorsan változó fázis esetén
). Tehát inhomogén esetben, lassan változó amplitudó és gyorsan változó fázis esetén 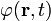 hordozza az információt, ez a geometriai optika. [6]
hordozza az információt, ez a geometriai optika. [6]

Írjuk be a fenti inhomogén megoldást a hullámegyenletbe!
Tehát:
A fentiek alapján tehát:
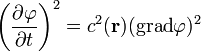
Ez az eikonál-egyenlet.
Ahol 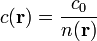 ,
, 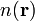 pedig a lokális (helyfüggő) törésmutató. A
pedig a lokális (helyfüggő) törésmutató. A 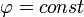 felületek adják meg az állandó fázisú felületeket, vagyis a hullámfrontokat. Az eikonál-egyenlet ezek mozgását írja le.
felületek adják meg az állandó fázisú felületeket, vagyis a hullámfrontokat. Az eikonál-egyenlet ezek mozgását írja le.
Fejtsük sorba a fázist: 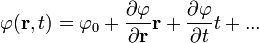
Majd írjuk be 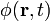 helyére:
helyére: 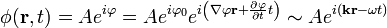
A fentiek fényében:
Az eikonál-egyenlet egyszerűsödik, ha 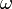 állandó, ekkor:
állandó, ekkor: 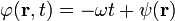 . Az jobb oldal utolsó tagjának neve "rövidített eikonál".
. Az jobb oldal utolsó tagjának neve "rövidített eikonál".
És:
E kettőből jön ez:
Az eikonál közelítés korlátai
A levezetés során a következő közelítéseket használtuk ki:
- Az amplitudó változása a hullámhosszal szorozva kisebb az amplitudónál,
- A hullámfelület görbületi sugara sokkal nagyobb a hullámhossznál,
- Az amplitudófelület görbületi sugara és a hullámhossz aránya sokkal nagyobb a hullámhossz és az amplidutó arányánál,
- A hullámfront lineáris méretei sokkal nagyobbak a hullámhossznál.
Ezek fényében az eikonál közelítés nem használható például fényforrások illetve fókuszpontok közelében, fény-árnyék határán. Továbbá mindezen feltételek erősen függenek a tekintett hullám hullámhosszától.
Analógia a klasszikus mechanikával
A fentiek fényében itt csak egy rövid táblázatban foglalnám össze a legfontosabbakat[8]:
| Pontmechanika | Geometriai optika | |||
| Hatásintegrál | 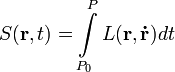 |
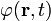 |
Eikonál | |
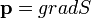 |
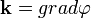 |
|||
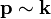 |
||||
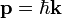 |
||||
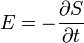 |
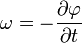 |
|||
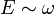 |
||||
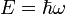 |
||||
| Hamilton-Jacobi egyenlet | 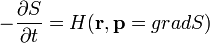 |
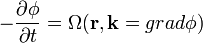 |
Eikonál-egyenlet | |
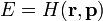 |
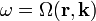 |
Diszperziós reláció | ||
| E mozgásállandó | 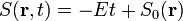 |
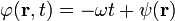 |
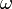 mozgásállandó mozgásállandó
| |
| Rövidített Hamilton-Jacobi egyenlet | 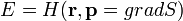 |
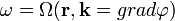 |
Rövidített eikonál-egyenlet | |
| Hamilton-féle kanonikus egyenletek | 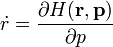 |
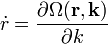 |
Csoportsebesség | |
| Hamilton-féle kanonikus egyenletek | 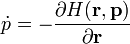 |
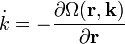 |
Hamilton-féle sugáregyenletek | |
| Maupertuis-elv | 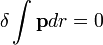 |
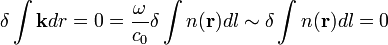 |
Optikai úthossz ~ Fermat-elv |
A Hamilton-féle sugáregyenletekből paraxiális közelítésben levezethető a lencsetörvény.
Megjegyzés: ugyanez Cserti József diáján megvan, (szerintem) kicsit átláthatóbban, ezért ezt az oldalt beszúrtam képként.

Ami az analógiából hiányzik
Pontmechanikában a Lagrange-függvény:
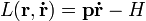 , ahol
, ahol 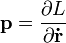 és
és 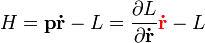
Keressük meg ugyanezt az optikában:
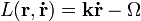 , ahol
, ahol 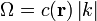 és
és 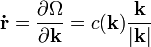
A fentiek alapján a Lagrange-függvény az optikában:
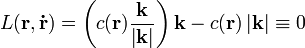 A Lagrange-függvény az optikában azonosan nulla.
A Lagrange-függvény az optikában azonosan nulla.
A mechanikai törésmutató meghatározásánál figyelni kell arra, hogy az analógiát ne a Fermat-elvből levezetett 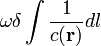 és ennek mintájára felírt
és ennek mintájára felírt 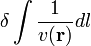 egyenlet között vegyük, mert
egyenlet között vegyük, mert 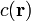 a fázissebesség, a mechanikai analógiában látott
a fázissebesség, a mechanikai analógiában látott 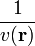 -ben a
-ben a 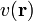 a csoportsebességnek feleltethető meg, melynek értéke az optikában:
a csoportsebességnek feleltethető meg, melynek értéke az optikában: 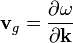 .
A helyes analógia a Fermat-elv és a Maupertuis-elv közötti megfeleltetés. Ezt végigszámolva a mechanikában a törésmutató értékére a következőt kapjuk:
.
A helyes analógia a Fermat-elv és a Maupertuis-elv közötti megfeleltetés. Ezt végigszámolva a mechanikában a törésmutató értékére a következőt kapjuk: 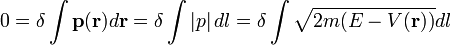 , mivel
, mivel 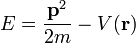 .
Ennek nyomán a törésmutató analogonja a mechanikában:
.
Ennek nyomán a törésmutató analogonja a mechanikában: 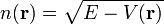 .
. 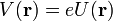 alkalmas megválasztásával elektrosztatikus lencsék/tükrök készíthetőek.
alkalmas megválasztásával elektrosztatikus lencsék/tükrök készíthetőek.
Részecske Optika  függ a részecske energiájától, diszperzív közeg
függ a részecske energiájától, diszperzív közeg 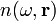 diszperzió
diszperzió
Éles képhez monoenergetikus nyaláb kell. Éles képhez monokromatikus fény kell. 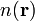 -re nincs korlát
-re nincs korlát n > 1, mert 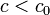
Paraxiális közelítés
Paraxiális közelítésben hengerszimmetrikus, tengelyközeli rendszereket vizsgálunk[10].
- A tengelytől való távolság kisebb, mint bármilyen releváns fókusztávolság, vagy rendszerméret.
- A sugarak szögei kicsik a tengelyhez képest.
Ebben a közelítésben: 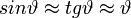
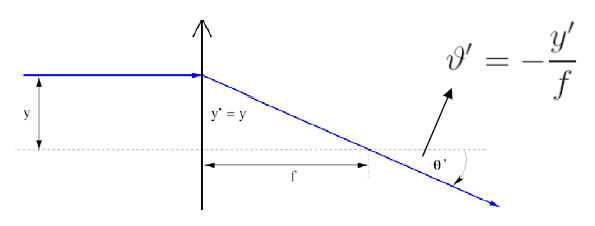
A fénysugarakat az optikai tengelytől mért (előjeles!) y távolsággal, és szintén az optikai tengellyel bezárt (előjeles![11]) szöggel jellemezzük.
Mátrix reprezentáció, leképezési törvények
Tetszőleges paraxiális rendszerben a fény terjedése leírható mátrix-, és vektorműveletekkel[12]:
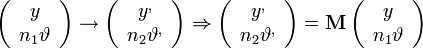
Három alapesetre felírhatunk mátrixokat, amiket aztán építőkövekként használhatunk összetett rendszerek leírására. Az alapesetek:
Szabad terjedés
A fény adott,  törésmuattójú közegben
törésmuattójú közegben  távolságot tesz meg. Ilyenkor a szög és a törésmutató nyilván nem változik (vagyis kettejük szorzata sem). Viszont
távolságot tesz meg. Ilyenkor a szög és a törésmutató nyilván nem változik (vagyis kettejük szorzata sem). Viszont 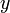
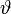 függvényében igen, mégpedig a következőképpen:
függvényében igen, mégpedig a következőképpen:
Ebből már könnyű felírni a szabad terjedés mátrixát:
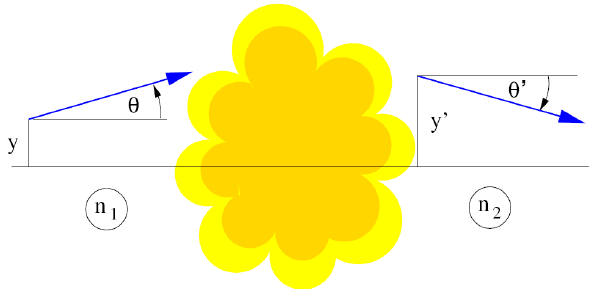
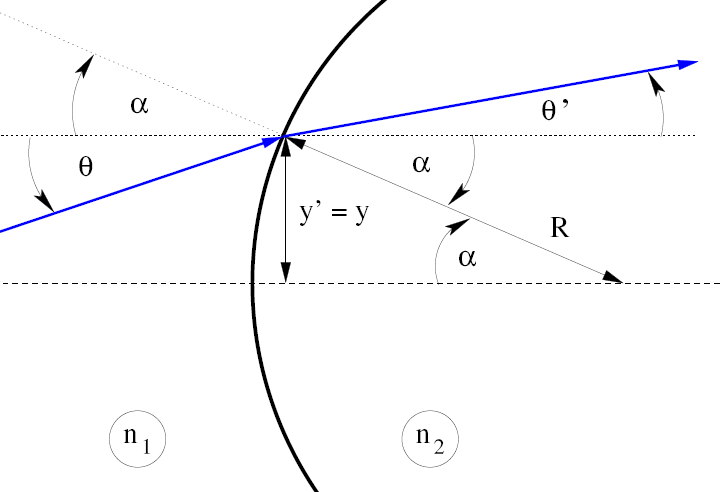
Törés gömbfelületen
A fény egy gömb felületű közeghatáron halad keresztül az ábra szerint. 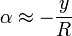 , és
, és 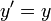 .
.
A Snellius-Descartes-törvény kis szögekre: 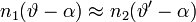
Vagyis: 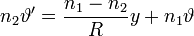
A törés mátrixa így:
Fontos észrevenni, hogy egy konvenciót hazsnáltunk: 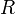 előjele a görbület irányától függően lehet pozitív, és negatív. Ha az ábrán látott eset áll fenn, akkor
előjele a görbület irányától függően lehet pozitív, és negatív. Ha az ábrán látott eset áll fenn, akkor 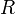 pozitív. Ha az ellenkező (a gömb középpontja a másik oldalon van), akkor negatív. Ez nem függ a fénysugár irányától! Ha a fénysugár megfordul, akkor is ugyanezt a konvenciót kell használni!
pozitív. Ha az ellenkező (a gömb középpontja a másik oldalon van), akkor negatív. Ez nem függ a fénysugár irányától! Ha a fénysugár megfordul, akkor is ugyanezt a konvenciót kell használni!
Mégegy megjegyzendő, hogy látszik, hogy 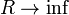 esetre visszakapjuk az egységmátrixot. Ennek így is kell lennie, hiszen ez a sík törőfelület, ahogy
esetre visszakapjuk az egységmátrixot. Ennek így is kell lennie, hiszen ez a sík törőfelület, ahogy 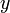 és
és 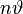 is állandó.
is állandó.
Visszaverődés gömbfelületről
Ez az eset hasonlít az elsőre (jelölések szempontjából is) azzal a kivétellel, hogy a fénysugár nem megtörik, hanem visszaverődik, és ugyanabban közegben halad tovább.
Szintén igazak az előbbi 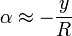 , és
, és 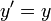 összefüggések, ám
összefüggések, ám 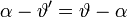 . Így:
. Így:
Így a visszaverő gömbfelület mátrixa:
Itt is lehet látni, hogy 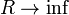 esetben a síktükröt kapjuk vissza.
esetben a síktükröt kapjuk vissza.
Összefoglalva
| Szabad terjedés | Törés gömbfelületen | Visszaverődés gömbfelületről |
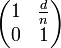 |
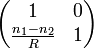 |
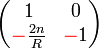
|
A mátrix reprezentációnál a fénysugarat követve a mátrixokat balról jobbra szorozzuk össze, így megkapjuk a teljes rendszert leíró optikai mátrixot. (Fontos, hogy a fénysugarat kövessük, mert menet közben pl. meg is fordulhat.) Tetszőleges paraxiális optikai rendszerre igaz, hogy 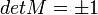 .
.
A leképezés fogalmai
- Fókuszpont: minden párhuzamos fénysugarat egy pontba gyűjtünk össze, y y'-től függetlenül valahol nulla lesz.
- Leképezés: egy pont leképezése során a pontból kiinduló fénysugarat
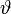 -tól függetlenül egy másik pontba gyűjtjük össze.
-tól függetlenül egy másik pontba gyűjtjük össze.
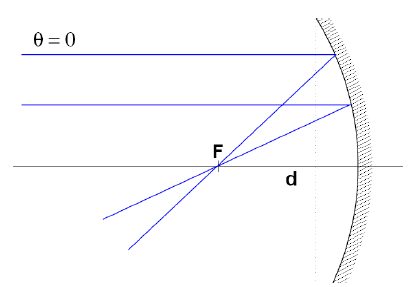
A gömbtükör fókusza
A rendszer leképezési mátrixa egy szabad terjedési mátrixból és egy visszaverődési mátrix szorzatából áll, balról jobbra összeszorozva:
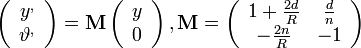 (Theta azért nulla, mert a tengellyel párhuzamosan érkeznek a sugarak:
(Theta azért nulla, mert a tengellyel párhuzamosan érkeznek a sugarak:
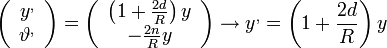 És mivel a fókuszpontban y' = 0, ezért
És mivel a fókuszpontban y' = 0, ezért 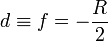
A gömbtükör leképezési törvénye
A rendszer leképezési mátrixa most egy tárgytól a tükörig tartó szabad terjedésből, egy visszaverődésből, és egy tükörtől a leképezésig tartó szabad terjedésből áll. A terjedési mátrix e három szorzata: 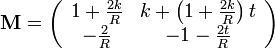
Mivel y' a leképezésnél független 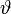 -tól, ezért a mátrix első sorának második eleme nullát ad, így (a gömbtükör fókuszára voantkozó összefüggés felhasználásával) megkapjuk a már ismert leképezési törvényt:
-tól, ezért a mátrix első sorának második eleme nullát ad, így (a gömbtükör fókuszára voantkozó összefüggés felhasználásával) megkapjuk a már ismert leképezési törvényt:
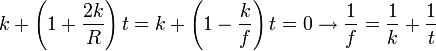
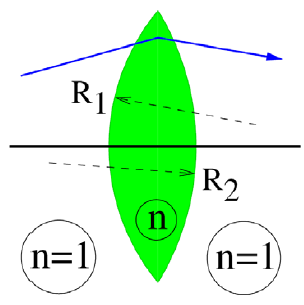
Vékony lencse fókusza
Egy vékony lencsénél két törőfelületről beszélhetünk, melyek két, 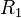 és
és 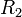 sugarú gömbfelületből állnak. A lencse anyagának törésmutatója n, a lencsét körülvevő közegé 1. A bal oldali törőfelület mátrixa
sugarú gömbfelületből állnak. A lencse anyagának törésmutatója n, a lencsét körülvevő közegé 1. A bal oldali törőfelület mátrixa 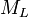 , a jobb oldalié
, a jobb oldalié 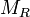 :
:
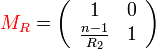
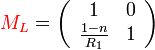
Ezek szorzata a rendszert leíró mátrix ezek szorzata (balról jobbra haladva, előjelesen):
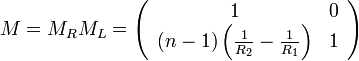
Az optikai tengellyel párhuzamosan beérkező fénysugár változása a rendszeren való áthaladás után:
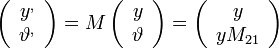
És mivel:
Így 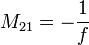 , tehát a fókusztávolság:
, tehát a fókusztávolság: 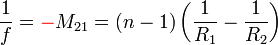 .
.
Vékony lencse leképezése
A vékony lencse leképezésének leírásához három mátrixot kell figyelembe vennünk, egyszer a tárgytávolságnyi szabad terjedés mátrixát, egyszer a törés mátrixát (a fent megismert összefüggés alapján), egyszer pedig a lencsétől a képtávolságig terjedő szabad terjedés mátrixát. Ezeket összeszorzova kapjuk meg a teljes optikai rendszer mátrixát, ami a következőképpen néz ki:
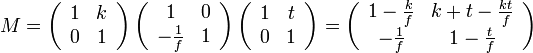
Mivel leképezésnél 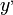 független
független 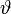 -tól, ezért
-tól, ezért 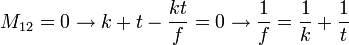 . Azaz itt is igaz a leképezési törvény.
. Azaz itt is igaz a leképezési törvény.
Összetett optikai rendszerek
Összetett optikai rendszereknél nem mindig igaz elsőre a leképezési törvény, de mint látni fogjuk, kis trükkel újra igazzá tehetjük.
- Sok egymás melletti vékony lencse esetén esetén a dioptriák
![\left( D = \frac{1}{f} [1/m] \right)](/images/math/d/8/4/d8455ea47916ed4b0f9b69ff4bf796b9.png) összeadódnak.
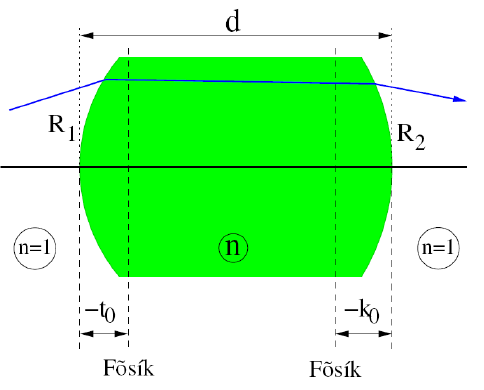
összeadódnak. - Vastag lencsék esetén szükség van az úgynevezett fősíkok bevezetésére. A fősíkok (lásd lejjebb) használatával a leképezési törvény újra igazzá tehető:
A tárgy-, és a képtávolságot a fősíkoktól mérve a leképezési törvény ismét igaz lesz. A fősíkok kiszámítása a következőképpen történik:
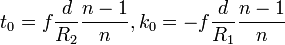
A fókusztávolságot vastag lencsék esetén a következő összefüggés adja meg (ez a lencsekészítők alapképlete). Egyébként ez három mátrix összeszorzásából ered: a vékony lencse jobb-, és bal oldali törőmátrixa közé be kell iktatni egy n törésmutatójú közegben történő szabad terjedés mátrixát (ezzel jelezzük, hogy vastag lencséről van szó). E három mátrix szorzatából lehet megkapni a vastag lencse, mint optikai rendszer mátrixát.
A fókusztávolságot lencsékre a rendszermátrix második sorának első eleméből lehet megkapni (mint fentebb láthattuk): 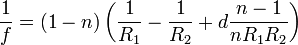
Általános leképezés
Teljesen általános leképezés esetén a leképezési mátrix: 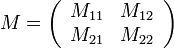 . Ezzel az a probléma, hogy nem lehet tudni, hogy hol a rendszer eleje és vége. Így módosítjuk egy kicsit:
. Ezzel az a probléma, hogy nem lehet tudni, hogy hol a rendszer eleje és vége. Így módosítjuk egy kicsit: 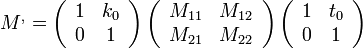
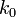 és
és 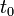 alkalmas megválasztásával (és kihasználva azt a tényt, hogy tetszőleges paraxiális optikai rendszer leképezési mátrixának determinánsa
alkalmas megválasztásával (és kihasználva azt a tényt, hogy tetszőleges paraxiális optikai rendszer leképezési mátrixának determinánsa 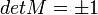 ):
): 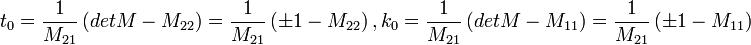
Így 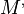 a következőképpen egyszerűsödik:
a következőképpen egyszerűsödik:
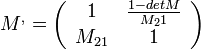 , ami - mivel
, ami - mivel 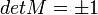 -
- 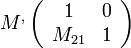 . Láttuk, hogy vékony lencséknél a mátrix éppen így néz ki, így meg tudjuk mondani a fókusztávolságot:
. Láttuk, hogy vékony lencséknél a mátrix éppen így néz ki, így meg tudjuk mondani a fókusztávolságot: 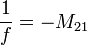 .
.
Optikai eszközök (távcső, mikroszkóp), felbontóképesség
Az optikai eszközök közül néhányról csak említés szintjén, és a címben szereplő távcsőről és mikroszkópról részletesebben fogok írni.
Vetítő, fényképező, nagyítólencse, szemüveg
- Vetítő: egy egyszerű lencse (és egy tükör) segítségével a tárgyról távoli, nagyított képet állít elő.
- Fényképező: távoli tárgyról készít kicsinyített, valódi képet tükrök, lencsék és blendék (fényerőszabályzók) használatával. A képek felvétele fényérzékeny anyagra, vagy újabban CCD-chipek segítségével valamilyen digitális tárolóegységre (általában memóriakártya) történik.
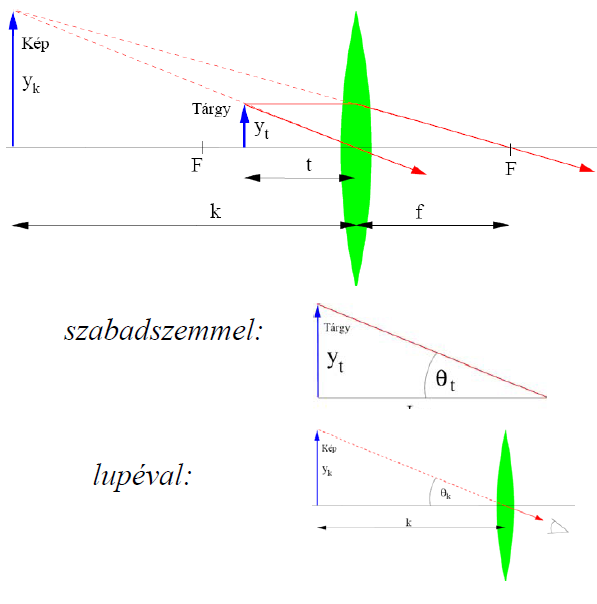
- Nagyítólencse (lupe): nagyított, virtuális (k < 0) képet készít a fókusztávolságnál közelebb lévő tárgyakról:
A lupe nagyító tulajdonságát két szempontból is érdemes megvizsgálni, az egyik a laterális nagyítás (képméret/tárgyméret):
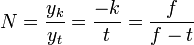 A másik a szögnagyítás:
A másik a szögnagyítás:
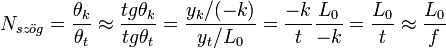 , mivel
, mivel 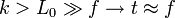
A lupe azért hasznos, mert a tisztánlátás távolsága körülbelül 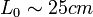 (viszonylag szubjektív adat), a lupe segítségével pedig ennél nagyobb távolságú tárgyakat is tisztán láthatóvá tehetünk.
(viszonylag szubjektív adat), a lupe segítségével pedig ennél nagyobb távolságú tárgyakat is tisztán láthatóvá tehetünk.
- Szemüveg: korrekciós lencse a szemlencse elé (a szemlencse kb. 60-64 dioptriás). Rövidlátás esetén a fénytörés túl erős, a kép a retina előtt fókuszálódik, szórólencse kell (D < 0). Távollátás esetén a fénytörés nem elég erős, a kép a retina mögött fókuszálódik, gyűjtőlencse kell (D > 0).
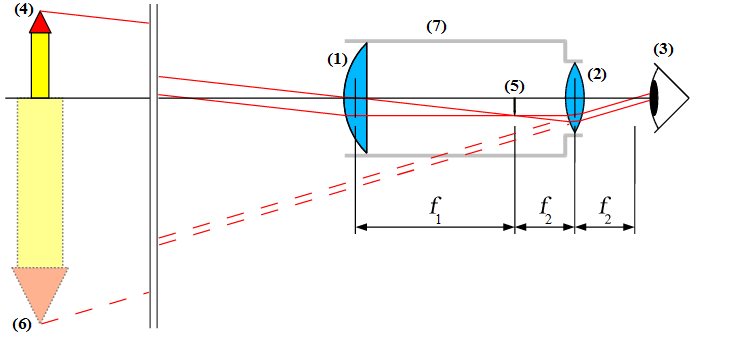
Mikroszkóp és felbontóképesség
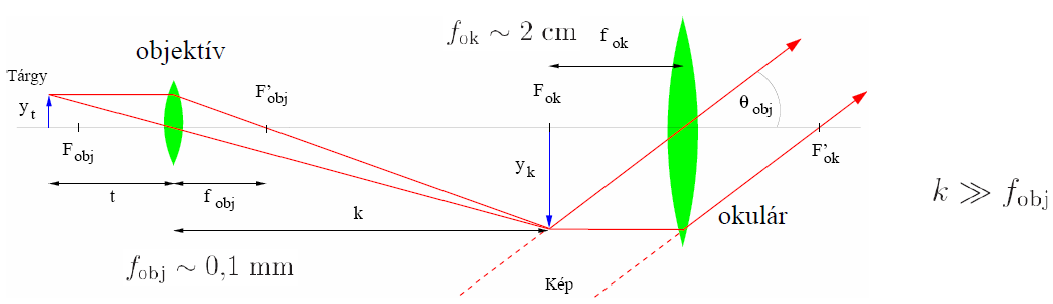
A lupe - bár sokmindenre jól használható - alapproblémája az, hogy nem tudjuk elég közel helyezni a szemünket. Ennek megoldására használjuk két lencsét, az egyik levetíti a képet (objektív), a másik pedig a lupe (okulár).
Egy mikroszkópban az objektív és az okulár fókuszsíkjai egymástól a mikroszkóp felépítése által meghatározott, állandó távolságban vannak. Ez az optikai tubushossz 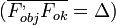 . Egy mikroszkópban ennek szabványos értéke 160 mm.[13]
. Egy mikroszkópban ennek szabványos értéke 160 mm.[13]
Az objektív laterális nagyítása: 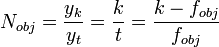 .
A mikroszkóp szögnagyítása:
.
A mikroszkóp szögnagyítása: 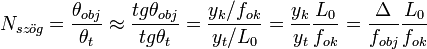
A tipikus nagyítás nagyságrendileg 1000 * 10.
Felbontóképesség
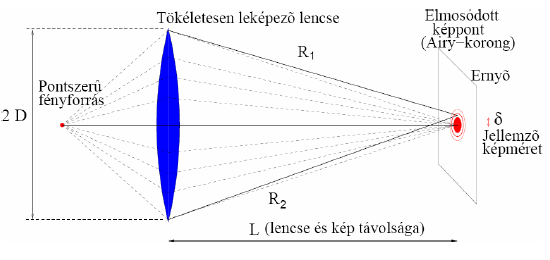
Az optikai eszközök felbontóképességét a hullámoptika közelíthetősége határolja be. Tökéletes leképezést feltételezve a Fermat-elv szerint minden képalkotásban résztvevő fényút optikai úthossza megegyezik. A hullámoptika szerint mindenféle pályán haladhat a fény, de ott lesz nagy az amplitudó, ahol körülbelül azonos fázisban érkeznek a hullámok.
Szögnagyítás: 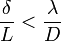 . Azaz minden lencse megfelel egy résnek, amely
. Azaz minden lencse megfelel egy résnek, amely 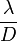 nagyságú diffrakciót okoz. Ez azt jelenti, hogy a mikroszkóp maximális felbontása:
nagyságú diffrakciót okoz. Ez azt jelenti, hogy a mikroszkóp maximális felbontása: 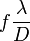 . A lencsére jellemző
. A lencsére jellemző 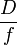 hányadost numerikus apertúrának nevezik. (Vannak más definíciók is a numerikus apertúrára, pl:
hányadost numerikus apertúrának nevezik. (Vannak más definíciók is a numerikus apertúrára, pl: 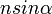 , ahol
, ahol 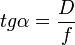 . D/f tipikus értéke 0,3 körüli, de a maximálisan elérhető felbontóképesség akár a hullámhossz nagyságrendjébe esik.
. D/f tipikus értéke 0,3 körüli, de a maximálisan elérhető felbontóképesség akár a hullámhossz nagyságrendjébe esik.
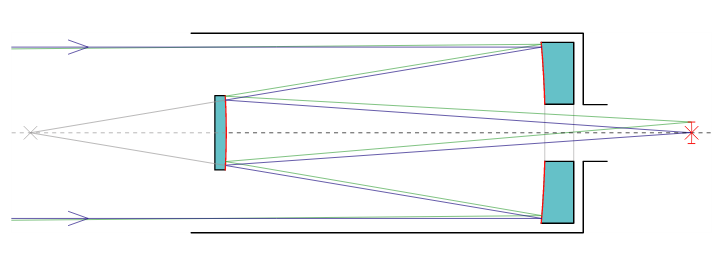
Távcső
A távcsövek konfokális (egybeeső fókuszponttal rendelkező) összetett lencserendszerek. A tárgy a végtelenben van, a kép is egy végtelen távoli pontban keletkezik. Laterális nagyításról tehát nincs értelme beszélni, csak szögnagyításról.
Mátrixoptikával úgy lehet leírni, hogy egy fókuszálás, majd szabad terjedés, majd még egy fókuszálás megy végbe, ez három mátrix szorzataként írható fel. Formálisan a fókusztávolság végtelen, ha a két lencse közötti távolság 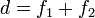 .
.
Szögnagyítás: 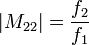
Távcső felbontása: 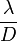 , ahol D a távcső lencséjének átmérője (csillagászati távcsöveknél 10 m nagyságrendű).
, ahol D a távcső lencséjének átmérője (csillagászati távcsöveknél 10 m nagyságrendű).
A különböző típusú távcsövekről:
- Kepler távcső (csillagászati távcső): két gyűjtőlencse,
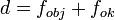
- Galilei-féle távcső (színházi távcső): az objektívje gyűjtőlencse, az okulárja szórólencse, és
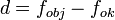 , egyébként ugyanaz, mint az előző.
, egyébként ugyanaz, mint az előző.
- Newton-távcső: hasonló elvi elrendezésa fentiekhez, ám ezúttal tükrökkel megvalósítva.
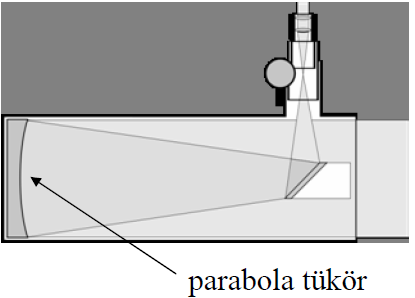
- Cassegrian-távcső: szintén tükrös távcső, az alábbi elrendezéssel.
A tükrös távcsövek előnyei a lencsésekkel szemben, hogy olcsóbban, nagyobb átmérőjű tükrök állíthatóak elő, ezáltal jobb felbontást lehet elérni. Valamint ugyanolyan felbontást kisebb méretű távcsővel lehet elérni.
Optikai jelenségek a természetben, kausztikák
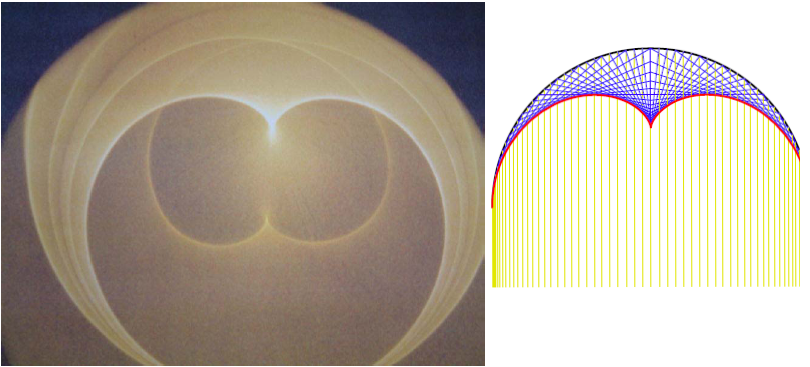
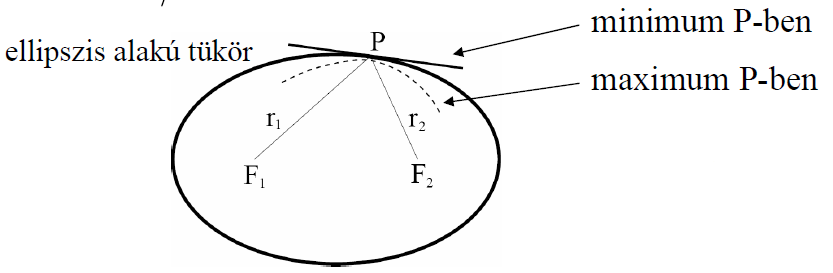
Először ejtsünk néhány szót a kausztikákról. A kausztika jelentése: görbesereg burkolója. Az optikában kausztikák akkor alakulnak ki, ha (közel) párhuzamos fénysugarak esnek egy nem sík felületre. Emiatt alakul ki a szivárvány, a tavakon naplementekor látható fényes sávok, valamint a henger alakú üvegalkalmatosságok alján látható furcsa fényfoltok.
- A szivárvány: feltételezzük, hogy a vízcseppek gömb alakúak (nem teljesen igaz, de a jelenség lényegileg nem változik sokat a gömbtől eltérő cseppalak esetén sem). Ha sok párhuzamos fénynyaláb érkezik rá egy irányból, akkor ezek a csepp határán megtörnek, majd a cseppben haladnak, annak falán (akár többször is) visszaverődnek, ezáltal (mivel a különböző színű (frekvenciájú) fénysugarak egy kicsit eltérően törnek ugyanolyan törésmutatójú közegben is) a különböző színek szétválnak, máshol lépnek ki cseppből néhány visszaverődés után. Ha sok ilyen cseppre esnek ugyanolyan irányból érkező párhuzamos fénysugarak, akkor a cseppekből a fény nagy része ugyanolyan irányban jut ki, ezt látjuk szivárványnak.
- Nagyobb tavaknál, például már a Balatonnál is lehet látni naplementekor a következő jelenséget: ha a vízre nézük, fényes csíkot látunk rajta, mintha a Nap ráfolyt volna a vízre egy sávon. Ennek oka, hogy a víz hullámzik, így a fénysugarak különböző irányba verődnek vissza a felületéről, ahogy azt az alábbi ábra is szemlélteti:
A fényes sávot azért látjuk, mert minden hullámnak van olyan része, ami a szemünk irányába veri vissza a fényt, így a sok különböző helyről szemünkbe jutó napfényt egy összefüggő fényes sávnak látjuk.
- ↑ Cserti József [1]
- ↑ Feynman: Mai fizika 3., 7-8. old.
- ↑ Feynman: Mai fizika 3., 10-12. old.
- ↑ Feynman: Mai fizika 3., 16-17. old.
- ↑ Optika és relativitáselmélet, 1. előadás, 16. oldal, [2]
- ↑ Optika és relativitáselmélet, 6. előadás, 2. oldal [3]
- ↑ Optika és relativitáselmélet, 6. előadás, 2. oldal [4]
- ↑ Optika és relativitáselmélet, 6. előadás, 4. oldal [5]
- ↑ Optika és relativitáselmélet, 6. előadás, 5. oldal [6]
- ↑ Optika és relativitáselmélet, 7. előadás, 5. oldal [7]
- ↑ Negatív: óramutató járásával megegyező, pozitív: óramutató járásával ellentétes.
- ↑ A teljes fejezet az Optika és relativitáselmélet 7. órájának fóliáiból lett összeálltva
- ↑ Havancsák Károly: Mérések a klasszikus fizika laboratóriumban, 188. old.
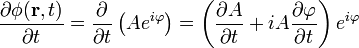
![\frac{\partial^2 \phi (\mathbf{r},t)}{\partial t^2} = \left[\frac{\partial^2 A}{\partial t^2} + 2i\frac{\partial A}{\partial t}\frac{\partial \varphi}{\partial t} + iA\frac{\partial^2 \varphi}{\partial t^2} - A\left(\frac{\partial \varphi}{\partial t} \right)^2\right]e^{i(\varphi (\mathbf{r},t))} \approx -A\left(\frac{\partial \varphi}{\partial t} \right)^2e^{i(\varphi (\mathbf{r},t))}](/images/math/0/5/0/05096837354b9899f362bf5506f71cf8.png)