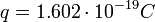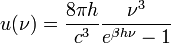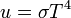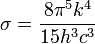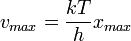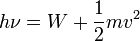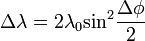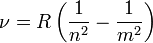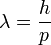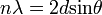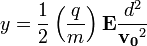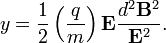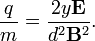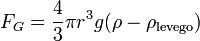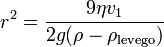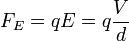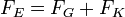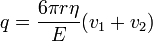„A kvantumelmélet alapvető kísérletei” változatai közötti eltérés
Alma (vitalap | szerkesztései) (→Az elektron fajlagos töltésének mérése: a Thomson-kísérlet) |
Alma (vitalap | szerkesztései) (→A Zeeman-effektus) |
||
| 75. sor: | 75. sor: | ||
==A Zeeman-effektus== | ==A Zeeman-effektus== | ||
| − | A spektrumvonalakat | + | A spektrumvonalakat mágneses térben vizsgálva Zeeman arra a megfigyelésre jutott, hogy azok különböző számú vonalakra hasadnak fel a mágneses tér nélkül látható egyes vonalakból. A jelenséget úgy magyarázták meg, hogy alapesetben a vonalak azonos energiájú elektron konfigurációknak felelnek meg, amelyek ezért nem különböztethetőek meg egymástól. Mágneses térbe helyezve azonban ez a degeneráció (egybeesés) megszűnik, hiszen minden kvantumszámban különbözniük kell az elektronoknak, és a vonalak felhasadnak (általában páratlan számú alvonalra). |
| − | Ha a párosítatlan spinű elektronok átmeneteit vizsgálták, akkor azonban még az előző módszerrel sem lehetett | + | Ha a párosítatlan spinű elektronok átmeneteit vizsgálták, akkor azonban még az előző módszerrel sem lehetett értelemezni a jelenséget, hiszen a kísérletek idején még nem volt ismert a spin, ezért ez utóbbi, páros felhasadásokkal járó effektust anomális-Zeeman effektusnak neveztél el. |
==Az elektron adatainak mérése== | ==Az elektron adatainak mérése== | ||
A lap 2011. június 23., 20:43-kori változata
Tartalomjegyzék
- 1 Hőmérsékleti sugázás és a Planck-törvény
- 2 Fotoeffektus
- 3 Compton-effektus
- 4 A Frank-Herz-kísérlet
- 5 A Rutherford-kísérlet
- 6 Atommodellek
- 7 A de Brogile hipotézis és a Davisson-Germer-kísérlet
- 8 A Stern-Gerlach-kísérlet
- 9 Az Einstein-de Haas-kísérlet
- 10 A Zeeman-effektus
- 11 Az elektron adatainak mérése
Hőmérsékleti sugázás és a Planck-törvény
A felmelegített testek sugároznak, mégpedig minnél nagyobb hőmérsékletűek, annál jobban. Az már sejthető volt a XIX. század végén is, hogy a hősugárzás is az elektromágneses sugárzás egy formája, ezáltal rá is a Maxwell-egyenletek érvényesek. Ez alapján próbálta meg Rayleigh és Jeans levezetni a sugázás energiasűrűségének frekvencia szerinti eloszlását. Ehhez egy zárt dobozban elhelyezett test által kisugrázott elektormágneses állóhullámok egyenleteit írták fel, és kihasználták az ekvipartíció tételét is, mint a különböző frekvenciáknak megfelelő oszcillátorokra jutó energiát leíró formulát. Az eredmények azonban nem voltak fényesek. A mérésekkel csak kis frekvencián egyeztek, továbbá a kapott eloszlás a nagy frekvenciák felé divergált, nem volt normálható. Ez az úgynevezett ultraibolya-katasztrófa.
Max Planck-nak volt azaz ötlete, hogy az oszcillátor energia esetleg nem folytonosan vehet fel értéket, hanem csak diszkrét csomagokban, ezáltal hibás az ekvipartíció kihasználása. A Planck által levezetett frekvenciaeloszlás:
Ez jól írja le a kísérleti eredményeket, továbbá normálható, és kihozható belőle másik két fontos összefüggés a Stefan-Boltzmann-törvény, amely a teljes kisugárzott teljesítményt írja le:
Továbbá kihozható belőle a sugárzási görbe maximumának hőmérséklet növekedés hatására bekövetkező eltolódása a nagyobb frekvenciák felé, ez a Wien-törvény:
Fotoeffektus
Többek között Lénárd Fülöp is vizsgálta azt a jelenséget, amelyben egyes fémek UV fénnyel történő megvilágításának hatására elektronok lépnek ki a fémből. A következő megállapításokat sikerült tenni:
- A kirepülő elektronok sebessége nem az intenzitástól, hanem a frekvenciától függ.
- A kirepülő elektronok száma az intenzitástól függ.
- Bizonyos küszöb frekvencia alatt semmilyen effektus nem mutatkozik.
A korabeli klasszikus elmélet szeirnt a fémbe behatoló fény energiáját szedi össze az elektorn és ezáltal tud kilépni. Ennek utánaszámolva teljesen használhatatlan eredményeket kapunk. A jelenséget csak úgy sikerült megmagyarázni, ha a fény kvantumokban éri el a fémet, és az által hordozott energiát egyben elnyeli az elektron, és az így nyert energia többlete fedezi a kilépésimunkát és a visszamaradó kinetikus energiát, ha azonban nem tudja fedezni a kilépésimunkát, akkor semi nem történik. A jelenség energiamérlege:
A jelenséget Einstein magyarázta meg.
Compton-effektus
Nagyfrekvenciájú elektromágneses sugárzások anyaggal való kölcsönhatását vizsgálva Compton arra a megfigyelésre jutott, hogy a sugárzás frekvenciája megváltozik az anyagon való áthaladáskor. A tárgyalt sugárzások energiája olyan nagy, hogy azok a kötési energiát messze felülmúlják, ezért a folyamat szabad elktronon való szóródásként tárgyalható, teljesen klasszikus részecske szemléletben is. Felírva az energia és az impulzusmegmaradást, kiszámolható a hullámhosszváltozás:
Ahol 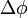 a foton eltérülésiszöge,
a foton eltérülésiszöge, 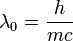 a foton Compton-hullámhossza, amely annak a fotonnka a hullámhossza, amelynek energiája megegyezik az elektron nyugalmi energiájával. A fenti formula a kísérletekkel jó egyezést mutat, és ezzel a fény korpuszkuláris természetét támasztja alá.
a foton Compton-hullámhossza, amely annak a fotonnka a hullámhossza, amelynek energiája megegyezik az elektron nyugalmi energiájával. A fenti formula a kísérletekkel jó egyezést mutat, és ezzel a fény korpuszkuláris természetét támasztja alá.
A Frank-Herz-kísérlet
Ebben a kísérletben gyorsított elektronokat ütköztettek ritka gázzal. Az ütközés térmentes környezetben történt, az elektronokat repülésük végén galvanométerrel mérték, azaz gyakorlatilag a beérkezett elektronok számát határozták meg. A kísérletben a gyorsító tér nagyságának függvényében vették fel a mért áramerősséget. Az eredmények szerint bizonyos helyeken az áramerősség maximumokat, majd erős visszaeséseket mutatott, és ezek a maximumok szabályos közönként követték egymást. A jelenséget így lehetett magayrázni, ha feltesszük, hogy az energiaátadás csak bizonyos energiáknál történik meg az atomok és az elektronok között. Ha nincs energia átadás, az ütközés rugalmas, ha van akkor rugalmatlan. Ebből az a következtetés vonható le, hogy az atomok elektronjai nem lehetnek tetszőleges energiájú állapotokban, azaz nem nyelhetnek el tetszőleges energiát, tehát a megengedett energiaszintjeik diszkrétek.
A Rutherford-kísérlet
Ebben a Rutherford által vezetett kísérletben arany fóliát bombáztak alfarészecskékkel és vizsgálták azok eltérülését kezdeti irányuktól. Egyszer a vizsgálatokat az alfarészek érkezésének irányából is megvizsgálták, és arra a megdöbbentő eredményre jutottak, hogy ugyan ritkán, de előfordul, hogy az alfarészecskék visszapattannak a fóliáról. Ismert volt hogy az atom kívülről elektromosan semleges, ugyanakkor tartalmaz elektronokat, amiből az kövekezik, hogy valamilyen pozitív töltésnek is jelen kell lennie a magban, hogy milyen formában, az még vitatott volt. Rutherford eredményei alapján azt lehettt kiszámolni, hogy ez a pozitív töltés az atom mretéhez képest kis helyen, és nagyon sűrűn koncentrálódik az atomban. Egyszerű Coulomb-téren (sztatikus elektromos téren) való szóródási számolásokból értelmezni lehetett a jelenséget.
Atommodellek
Rutherford kísérlete alapján maga is kidolgozott atommodellt az általa leírt szerkezettel összhangban. A Naprendszer analógiáját hasnzálta, úgy képzelte el, hogy az elektronok a pozitív mag körül keringenek, és gravitációs helyett az elektromos erő tartja őket pályán. Ez a feltevés azonban igen rövidéletű volt, hiszen a klasszikus értelmezésben az elektron körpályán haladva sugároz, aminek következtében energiát veszít, és egy idő után beleesik a magba, továbbá az így kisugárzott spektrum folytonos kéne legyen, a valóságban azonban vonalas spektrumokat figyeltek meg.
Ezen vonalas spektrumok leírására tapasztalati törvényt sikerült felírni:
Ezeket a vonalakat nem sikerült megnyugtatóan megmagyarázni, azonban Niels Bohr-nak sikerült ezeket összhangba hoznia a Rutherford-kísérlet eredményeivel és egy atommodellbe egyesítenie a jelenségeket. Feltette a következő posztulátumokat:
- Az atomban mozgó elektronok csak diszkrét pályákon mozoghatnak, a pályákhoz tartozó impulzusmomentum csak diszkrét értékeket vehet fel.
- Ezeken a pályákon tartózkodó elektronok nem sugároznak, sugárzás csak két fentebb definiált pálya közötti átmenetkor történik.
- Az átmenetkor kisugárzott foton energiája a két pálya energiájának különbsége.
Ezeknek a feltételezéseknek Bohr nem tudott hátteret biztosítani, azonban számos jelenséget meg tudott velük magyarázni annak ellenére, hogy a klasszikus gondolkodástól teljesen idegennek hatottak. A vázolt elmélet azonban a Hidrogén, és az ahhoz hasonló alkálifémek spektrumait igen jól leírta. Értelemzni lehetett vele a Frank-Hertz-kísérlet eredményeit is. Azonban az elméletnek igen jelentős korlátai voltak: gyakorlatilag kvantitatíve csak a hidrogénre adott jó leírást a többi atomra nem, és a spektrumvonalak intenzitása sem jött ki. Továbbá a spektrum finomszerkezetét sem magyarázta meg, és az impulzusmomentum függését a kvantumszámoktól is rosszul adja meg. Ennek ellenére alapvető jelentősége volt a mikrovilág kutatásának fellendülésében.
A de Brogile hipotézis és a Davisson-Germer-kísérlet
Planck foton hipotézise alapján de Brogile arra az elméleti feltevésre jutott, hogy nem csak a fény, de az anyagi alkotók is hullámtulajdonsággal rendelkezhetnek, és a hozzájuk rendelhető hullámhossz:
Ezt az elméleti ötletet támasztotta alá Davisson és Germer kísérlete, amelyen a kistályos anyagok vizsgálatánál jólbevált Bragg-féle diffrakciós képletet tudták igazolni elektronokra is:
A feltétel alapján n egész értékeire erősítést kell látni az interferenciaképben. A kísérleteket Nikkel kristályon végezték, amelynek simert volt a d rácsállandója, és de Brogile hullámhossz képletét felhasználva ismert energiájú elektronokra valóban jó egyezés mutatkozott. Ez a kísérlet alapvető fontosságú az anyag hullámtermészetének igazolásában.
A Stern-Gerlach-kísérlet
Ismert volt klasszikus elektrodinamikából, hogy a töltött részecskék eltérülnek mágneses térben. Ismert volt az is, hogy a köráramokhoz mágneses momentum rendelhető, így azok is kölcsönhatnak a mágneses térrel. Stern és Gerlach tulajdonképpen a Bohr-elméletet kívánta tesztelni, ugyanis a jóslat értelmében az elektron pályáihoz tartozó impulzusmomentum csak diszkrét értékeket vehet fel, amiből az is következik, hogy ehhez diszkrét mágneses momentum tartozik. A kísérletben ezüst atomokat inhomogén mágneses térben térítettek el. Eredményül azt kapták, hogy az atomok a klasszikus folytonos eltérülés helyett diszkrét sávokba rendeződtek, ami a Bohr-féle kvantáltságot támasztotta alá.
A későbbiekben megvizsgálták a kísérletben, hogy mi történik ha elektronokkal (vagy hidrogén atomokkal) végzik el a kísérletet. Ekkor is kvantáltság jelentkezett az elhajlási képben, ami arra vezetett, hogy a részecskéknek van valamilyen saját mágneses momentumként viselkedő jellemzője is. Ez vezetett a spin fogalmának kialakulásához. A későbbiekben megmutatták, hogy az atommagnak is van kvantált mágneses momentuma, ami a magspinből származik.
Az Einstein-de Haas-kísérlet
Ebben a kísérletben egy felfüggesztett ferromágneses hengert vizsgáltak, amely egy tekercsben helyezkedett el, és torziós forgásra volt képes a felfüggesztés körül. Ha a tekercsre elektormos impulzust adtak, a ferromágnes elfordult. Azonban az impulzusmomentum megmaradásának értelmében valaminek el kellett vinnie az impulzusmomentum ellentétes irányú részét. Az eredményeket csak úgy tudták megmagyarázni, ha feltételezték, hogy az elektronok spinje ugyanolyan természetű, mint a klasszikus impulzusmomentum, és a mágneses hatása is van. A kvantitatív elemzésekből kiderült, hogy egy kettes faktor különbség van a klasszikus köráram értelemzés és a mérési eredmények között. Ez egy újabb érv volt a kvantummechanikai tárgyalás sikeressége mellett.
A Zeeman-effektus
A spektrumvonalakat mágneses térben vizsgálva Zeeman arra a megfigyelésre jutott, hogy azok különböző számú vonalakra hasadnak fel a mágneses tér nélkül látható egyes vonalakból. A jelenséget úgy magyarázták meg, hogy alapesetben a vonalak azonos energiájú elektron konfigurációknak felelnek meg, amelyek ezért nem különböztethetőek meg egymástól. Mágneses térbe helyezve azonban ez a degeneráció (egybeesés) megszűnik, hiszen minden kvantumszámban különbözniük kell az elektronoknak, és a vonalak felhasadnak (általában páratlan számú alvonalra).
Ha a párosítatlan spinű elektronok átmeneteit vizsgálták, akkor azonban még az előző módszerrel sem lehetett értelemezni a jelenséget, hiszen a kísérletek idején még nem volt ismert a spin, ezért ez utóbbi, páros felhasadásokkal járó effektust anomális-Zeeman effektusnak neveztél el.
Az elektron adatainak mérése
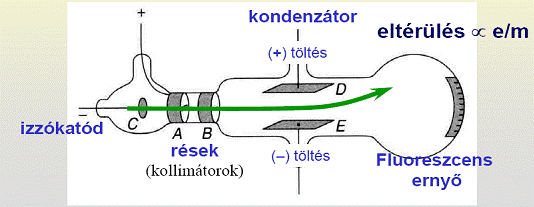
Az elektron fajlagos töltésének mérése: a Thomson-kísérlet
Tegyük fel, hogy a 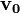 kezdősebességű, adott fajlagos töltésű részecske a
kezdősebességű, adott fajlagos töltésű részecske a 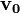 sebességre merőleges
sebességre merőleges 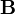 indukcióvektorral jellemzett mágneses térben mozog és az eltérülés kicsi. Ekkor a gyorsulás közelítőleg állandó, merőleges a sebességre, és nagysága:
indukcióvektorral jellemzett mágneses térben mozog és az eltérülés kicsi. Ekkor a gyorsulás közelítőleg állandó, merőleges a sebességre, és nagysága: 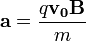 . Ha mágneses tér helyett annak irányára és a részecske sebességének irányára merőlegesen homogén, kellően kicsi elektromos teret kapcsolunk be, akkor a részecske ugyanolyan irányban térül el közel állandó,
. Ha mágneses tér helyett annak irányára és a részecske sebességének irányára merőlegesen homogén, kellően kicsi elektromos teret kapcsolunk be, akkor a részecske ugyanolyan irányban térül el közel állandó, 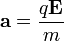 gyorsulással. Ha ezt a két teret egyszerre alkalmazzuk megfelelő erősséggel, akkor elérhető, hogy a részecske ne térüljön el.
gyorsulással. Ha ezt a két teret egyszerre alkalmazzuk megfelelő erősséggel, akkor elérhető, hogy a részecske ne térüljön el.
Thomson 1897-ben a következő módon határozta meg az elektron fajlagos töltését:
Megmérte egy adott sebességű elektronnyaláb eltérülését a sebességre merőleges elektromos térben:
(mivel körülbelül 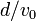 ideig állandó gyorsulással repül az elektron), majd a
ideig állandó gyorsulással repül az elektron), majd a 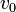 -ra és
-ra és 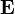 -re merőleges
-re merőleges 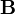 indukciójú térrel visszaállította a nyalábot eredeti helyzetébe.
Ekkor a két tér sebességszűrőként működik, csak a:
indukciójú térrel visszaállította a nyalábot eredeti helyzetébe.
Ekkor a két tér sebességszűrőként működik, csak a: 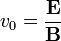 sebességű részecskék haladnak tovább egyenesen. Ezt felhasználva a sebesség bejövő elektronok sebessége kiküszöbölhető az eltérülési képletből:
sebességű részecskék haladnak tovább egyenesen. Ezt felhasználva a sebesség bejövő elektronok sebessége kiküszöbölhető az eltérülési képletből:
Ebből kifejezhető a fajlagos töltés:
Az elektron töltésének és tömegének mérése: A Millikan-kísérlet
Cél: az elektromos tér változtatásával és a nehézségi erő kimérésével meghatározni az elektron töltését. Millikan ehhez két fémlemez közé juttatott olajcseppeket (az olajcseppek porlasztáskor töltéshez jutnak). A lemezek közötti feszültség változtatásával a töltött cseppek töltését a következőképpen mérte meg:
A folyamat kezdetén – mivel ekkor még nem aktiváljuk az elektromos mezőt – az olajcseppek szabadon esnek a lemezek között. A cseppek rövid idő alatt elérik a végsebességüket a kamrában lévő levegőrészecskékkel való ütközés következtében létrejövő súrlódás miatt. Ekkor aktiváljuk az elektromos mezőt, és ha az megfelelően nagy, néhány részecske (a töltéssel rendelkezők) emelkedni kezdenek (mivel a rájuk ható FE elektromos mező által az olajcseppre kifejtett, "felfelé" ható erő nagyobb lesz, mint a "lefelé" ható G nehézségi erő). Egy megfelelőnek tűnő olajcsepp kiválasztása és a mikroszkóp látómezejének közepére mozgatása után a feszültség kikapcsolgatásával elérjük, hogy a kiválasztott cseppen kívül minden más csepp leessen. A kísérlet további részében tehát már csak ezzel az egy cseppel dolgozunk.
A kiválasztott cseppet hagyjuk, hogy szabadon essen. Kis tömegéből kifolyólag gyorsan eléri a végsebességét, amikor már nem hat rá elektromos erő, vagyis a gravitációs erő kiegyenlítődik a közegellenállással, ami meghatározható a Stokes-törvényből:
- ahol v1 a csepp végsebessége, η a levegő viszkozitása, r pedig a csepp sugara. A súlyát a következő képletből számoljuk (beleszámítva a felhajtőerőt):
Ezt a két erőt kiegyenlítve a csepp sugarára a következőt kapjuk:
Most bekapcsoljuk az elektromos teret, és olyan erősre állítjuk, hogy a csepp egy új v2 sebességgel emelkedjen. A rá ható erők: gravitáció, a Stokes-erő és az elektromos erő:
ahol a V a feszültség, a d pedig a két lemez közötti távolság. A három erő kiegyenlíti egymást:
ha behelyettesítjük az előző mérés ereményét, akkor megkapjuk a csepp töltését:
Millikan azt tapsztalta, hogy a kapott q értékek egy bizonyos érték többszörösei, ez pedig az elektron töltése: