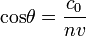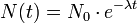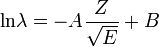A magfizika alapjai
Tartalomjegyzék
Az izotóp térkép
Az anyagot az atomok alkotják. Ezeknek a lényegi tulajdonságainak egyrészét az atommag összetétele határozza meg, a másikfelét a jelenlevő elektronok száma. Az atomokat a periódusos rendszerben foglalhatjuk össze a kémiai tulajdonságaik alapján csoportoítva. A magfizikában azonban célszerűbb az atommagokat, mint neutronok és protonok kombinációját tekinteni. Az izotóptérképen az egyik tengelyre a neutronok számát, a másik tengelyre a protonok számát (a rendszámot) mérik fel. Ezen az ábrán a stabil magok az origó közelében a 45-fokos tengely mentén sorakoznak, távolodva azonban a neutron többlet felé hajlanak el.
Atommagok tömege
Az atommagok tömegét a protonok és neutronok adják, de ennél valójában kicsit könnyebbek a tömegdefektus miatt.
Mérete és alakja
Az atommagok méretét és alakját szórási kísérletekkel lehet megmérni, más összetett bombázórészecskékkel a magerők eloszlása is feltérképezhető. Az átlagos méret 1 fm körül alakul.
Kötési energiája
Az atommagok kötés energiáját az egy nukleonra jutó kötésienergiával jellemezzük. Ez a mennyiség a rendszám növelésével először meredeken csökken, a vasnál minimumot ér el, utána lassan emelkedik. Ez azt jelenti, hogy a könnyű elemek egybeolvadása (fúzió) és a vasnál nehezebb elemek bomlása energiatermelő folyamat.
A magerők kvalitatív jellemzése
A magerők a nukleonok között hatnak, ezek tartják össze az atommagot. Ez az erőhatás az erőskölcsönhatás másodlagos megnyilvánulása, hasonlóan a Van der Waals-féle indukált dipólus kölcsönhatáshoz. Az erőskölcsönhatást a kvantumszíndinamikával igen jól le lehet írni - aszimptotikus esetben nagy energián. Azonban a magfizikailag érdekes energiaskálákon az elmélet nem perturbatív, így "ab inicio" számításokat igen nehéz végezni. Ezekből kifolyólag a magerők leírására igencsak kvalitatív, és fenomenologikus.
Kvalitatív tulajdonságai:
- Nukleonok között hat.
- Kis távolságokon erősen taszító, ettől távolabb vonzó, de gyorsan lecseng.
- Elektromos töltésfüggetlen.
- A közvetítő részecskéjét a pionnal azonosítjuk.
Ez utóbbi állítást úgy kell elképzelni, hogy itt is gluonok közvetítik a kölcsönhatást, csak időnként egy kvark-antikvark csere történik, amely felfogható egy pionként is, lásd: itt.
A Yukawa féle 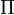 -mezon(*)
-mezon(*)
Yukawa a magerők leírására javasolta az alábbi alakú potenciált:
ahol R az a karakterisztikus hossz, amin a magerők hatása lecseng. Nyilvánvaló, hogy ez a potenciál a közeli taszító részt nem tartalmazza, így egyfajta aszimptotikus közelítése a magerők tényleges potenciáljának. A Yukawa-potenciál elektrodinamikai analógiával a következő hullámegyenletből származtatható:
Ennek síkhullámmegoldásait keresve 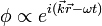 a következő diszperziós relációt kapjuk:
a következő diszperziós relációt kapjuk:
Ez összevetve a szokásos relativisztikus diszperziós relációval
Megbecsülhető a közvetítő részecske, a 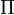 -mezon tömege. Az, hogy a közvetítő részecskének van tömege, az okozza a kölcsönhatás rövid hatótávolságát.ű
-mezon tömege. Az, hogy a közvetítő részecskének van tömege, az okozza a kölcsönhatás rövid hatótávolságát.ű
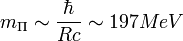 ha R=1fm-vel számolunk. A töltött pion tényleges tömege 140MeV, a semlegesé 135 MeV.
ha R=1fm-vel számolunk. A töltött pion tényleges tömege 140MeV, a semlegesé 135 MeV.
A cseppmodell
A cseppmodell az atommagokat összenyomhatatlan folyadékként képzeli el, amelynek az összenyomhatatlanságát a Pauli-féle kizárási elv biztosítja. Ebből és más fenomenologikus érvekből kifolyólag az atommagoknak forgási-ellipszoidot tételezünk fel, amelynek forgási tengelye a spinnel esik egybe.
A félempírikus kötési formula
A félempírikus kötési formula az atommagok kötöttségét írja le fenomenologikus alapon, az elméltei megfontolásokból bevezetett tagokat a mérésekhez fittelve. Eszerint a kötési energia a következőképpen írható:
Az első tag a térfogati tag, ez egyenesen arányos a nukleonok számával (A). Ez a tag dominálja az összeget, és ez bizonyíték arra is, hogy a megerők rövidhatótávolságúak. Ha hosszúhatótávolságú lenne, akkor ugyanúgy négyzetesen menne a töltéssel, mint az elektromos vagy gravitációs. A második tag a felületi tag, ez azt jellemzi, hogy a felületen levő nukleonoknak kevesebb szomszédjuk van, ezért ezek kevésbé kötöttek (hasonló a felületi feszültséghez). A harmadik tag a Coulomb-tag, amely az elektrosztatikus taszítás miatti csökkenést írja le. A negyedik tag a Pauli-féle szimmetria tag, ez a kizárási elv miatt bukkan fel hiszen a nukleonok is fermionok, így nem tartózkodhat azonos állapotokban egy részecskénél több. Az ötödik tag a párenergia, a spincsatolást próbálja meg figyelembevenni, és a páros feltöltődés kedvezőbb mivoltát (kedvező helyzet, ha egy állapotban csak spinben különböző részecskék vannak, ezért kedvező a párosság, ha a protonok és neutronok száma is páratlan az negatív előjelet ad, az előző két eseten kívül pedig 0).
Ez a látszólag mondvacsinált formula jól leírja a legtöbb periódusosrendszerbeli magot, a legkönnyebbek kivételével, átlagosan kb. 5% pontossággal, csupán 5 paraméterrel, ezért széleskörben elterjedten használják. Hátránya, hogy nem ad számot a mágikus számok megjelenéséről.
Maghasadás
A korábban bevezetett kötésienergia rendszám szerinti eloszlásából következik, hogy a nehéz atommagok, ha könnyebbekbe tudnak elbomlani, akkor energia szabadul fel, tehát ez utóbbi állapot mélyebb energiájú. A nehéz atommagok önmaguktól is elbomolhatnak alfa, vagy bétabomlás segítségével. Ezt a folyamatot spontán bomlásnak nevezzük. Az atombombában és az atomerőművekben indukált bomlásról beszélünk, itt termikus neutronokkal bombázva bontják szét az atommagokat, ezáltal a reakció hevesebb, de egyben irányítható is marad. A legfontosabb alkalmazott hasadóanyagok a Plutónium 239-es izotópja, és az Urán 235-ös izotópja.
Magfúzió
A kötésienergia kis rendszámok esetén a rendszám növelésével csökken, azaz itt energetikailag kedvező, ha a kisebb atommagok nagyobbakká egyesülnek. Itt azonban le kell győzni a Coulomb-potenciál taszítását, így ehehz igen nagy hőmérséklet és sűrűség kell. Ez a folyamat a csillagokban számottevő, de jelenleg folynak kísérletek erőművi alkalmazások kifejlesztésére.
Sugárzás és anyag kölcsönhatása
Részecskék és anyag kölcsönhatása
A különböző energiával haladó részecskék álló anyaggal való kölcösnhatása igen sokféle lehet, azonban a makroszkópikus hatás közös: a mozgó részek energiát vesztenek, miközben az általuk leadott energia más részecskéknek adódik át valamilyen formában. Ebből kifolyólag a legyakrabban tárgyalt mennyiség az egységnyi úton leadott energia. Legegyszerűbb közelítésben különböztessük meg a sugárzásos és ionizációs energiaveszteséget, valamint különítsük el az elektronokat, mint könnyű, elemi részecskéket a többi nehezebb és összetett részecskétől. Fontos megjegyeznim hogy az itt részletezett foylamatok töltött részecskékre értendőek.
- A nehézrészecskékre sokkal jelentősebb az ionizációs energia leadás kis energián
- Nagyonnagy energián itt is szerepet játszik a fékezési sugárzás, és a Cserenkov-sugárzás.
- Könnyű részecsskékre (elektornokra) az fenti elkülőnülési határ alacsonyabban van, így már kisebb energián is jelentős a fékezésisugárzásuk, de ezek is tudnak ionizálni.
Az ionizációs folyamatok általában az anyagban a elektonrburokkal való kölcsönhatás eredményei, legegyszerűbben a mozgásienergia átadódik az elektronoknak a burokban.
Nehéz részecskék ionizációs leírására a Bethe-formula használatos, amely nemrelativisztikus energiákra a köveketező:
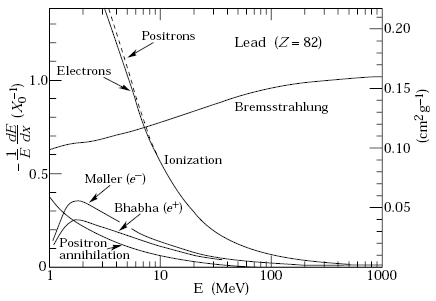
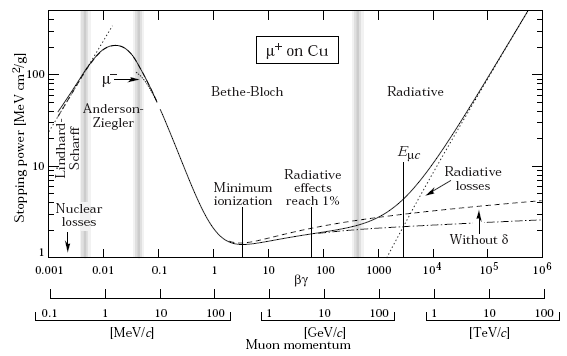
A lefontosabb arányosságok a formulából a rendszám négyzetével (Z) és a sebesség négyzetével fordítottan való függés. Ebből az kövektezik, hogy az energialeadási görbe a sebesség növelésével csökkenő tendenciát mutat. Ezután más effektusok kezdenek szerepet játszani (polarizáció, sugárzási energia veszteség) ezért egy minimum után újra emelkedni kezd a görbe:
Elektronokra azt érdemes tudni, hogy az ionizációval leadott energia logaritmikusan függ az energiától, míg a fékezésisugárzásos energialeadás lineárisan, ezért ez utóbbi dominál már pár 10 MeV felett.
A nehéz részecskék sugárzásos energialeadásából a legfontosabb jelenség a Cserenkov-sugrázás, amely akkor jön létre, ha a nagyenergiájú töltött részecske sebessége meghaladja az adott közegbeli fénysebességet. Fontos, hogy a közeg szigetelő legyen. Ekkor a töltött részecske által megrántott közegbeli dipólok sugárzást bocsájtanak ki, amely kúpfelületű frontba rendeződik. Ennek a kúpnak a nyílásszöge:
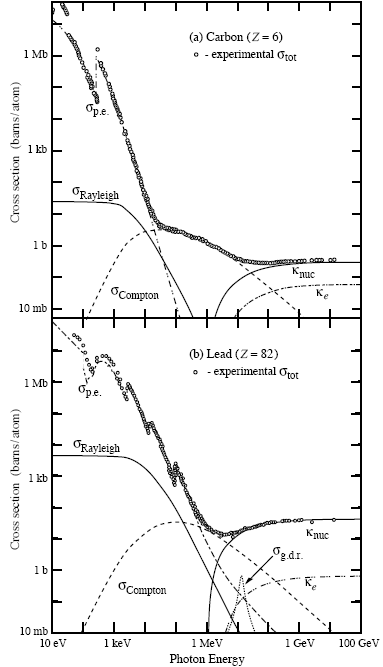
ahol n a közeg törésmutatója, v a részecske sebessége, 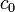 a vákuumbeli fénysebesség. A Cserenkov-sugárzás jellegzetes kék színű, és intenzitása még a nagyobb frekvenciák felé nő, de a gamma spektrumban levág.
a vákuumbeli fénysebesség. A Cserenkov-sugárzás jellegzetes kék színű, és intenzitása még a nagyobb frekvenciák felé nő, de a gamma spektrumban levág.
Gammasugárzás és anyag kölcsönhatása
Az elektromágneses hullámok anyaggal való kölcsönhatásában a következő folyamatok játszanak fontos szerepet:
- Compton-folyamat: foton fugalmatlan szóródása elektrononm ekkor a foton energiát ad le az elektronnak.
- Fotoeffektus: az elektronburokban egy elektron éppen egy másik pályára való átmenethez szükséges energiát hordozó fotonnal találkozik. Ekkor a foton elnyelődik, és az elektron gerjesztett állapotba kerül.
- Párkeltés: egy nagyenergiás foton (E > 2 x 511 keV ) elektron-pozitron párt hoz létre. Szükséges hozzá külső tér (vákuumban nem jön létre).
Alacsony energián a fotoeffektus dominál, jellegzetes csúcsokkal, hiszen keskeny energiasávban tud csak elnyelni. Közepes energián a comptoneffektus dominál, ez folytonos spektrummal rendelkezik, az energiával fordítottan arányos megközelítőleg. Nagyenergián a párkeltés kezd el dominálni. Továbbá a rendszám függések is jellegzetesek: a Compton-effektus valószínűsége arányos a rendszámmal, a fotoeffektusé azonban a rendszám 5. hatványával!
Radioaktivitás
Összefoglalóan radioaktivitásnak nevezzük atommagból eredő sugárzásokat. Ezek többnyire valamilyen atommagátalakulásos, vagy átrendeződéses folyamat eredményei.
Amikor az átalakulás külső hatás nélkül játszódik le, akkor spontán folyamatról beszélünk. Ezeket teljesen véletlenszerűnek tekintjük, a bomlások Poisson-folyamat szerint fordulnak elő, amiből következik, hogy két bomlás között exponenciális idő tellik el, és a következő bomlásig hátralevő idő is exponenciális eloszlású. Ez az exponenciális bomlástörvény:
ahol 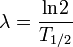 a bomlási paraméter, T a felezésiidő. Belátható, hogy az átlagos élettartam:
a bomlási paraméter, T a felezésiidő. Belátható, hogy az átlagos élettartam: 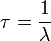
Radioakív bomlások
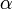 -bomlás
-bomlás
Az atommagokra vonatkozóan említettük, hogy csak igen fenomenologikus elméletek állnak rendelkezésünkre a magok leírására. Ezek közül igen jólműködőnek tűnik az a leírásm amely az atommagokban kisebb, erősen kötött alrészekkel számol. A kötésienergia-eloszlása alapján ismert, hogy a hélium atommagjának igan magas a kötési energiája, ezért célszerű azt feltételezni (és kis magok esetében jól működik), hogy az összetettebb atommagok hélium atommagok, és más részek szuperpozíciójából tevődnek össze.
Ismert azonban kvantummechanikából az alagút-effektus. Eszerint egy véges potenciálgátakközé zárt részecske bizonyos valószínűséggel ki tud jutni a gát mögül annak ellenére, hogy az energiája kisebb és kisebb is marad a gát magasságánál. Ha az alfarészt, mint a magerők potenciáljába zárt részecskét tekintjük, ugyan ez a lehetőség fennáll. Ezt a folyamatot, amelyben alfarészecske hagyja el az atommagot, 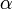 -bomlásnak nevezzük.
-bomlásnak nevezzük.
Az alfabomlás energiája igen behtárolt, maximum 10 MeV körül alakul. Nagyméretű atommag révén könnyen lefékeződik és leadja energiájátm így kicsi az áthatoló képessége.
Az alfarészecskék energiájára Geiger-Nuttal tapasztalati törvény fontos jellemző, amely a felezési időket és a kibocsátott alfarészecskék energiáit kapcsolja össze:
ahol A és B konstansok, Z a rendszám, E az alfarészecske energiája. Ez a törvény azt foglalja magában, hogy a sok nagyságrendet átfogó felezési idők igen kis különbségeknek felelnek meg a kisugárzott alfarészecske energiájában.
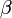 -bomlás típusai
-bomlás típusai
β-bomlásnál egy u-d kvark alakul át egymásba, amely reakció közben egy töltött W bozon csere is lezajlik, tehát a β-bomlások a gyengekölcsönhatás által vezérelt reakciók. Felszabadul továbbá egy elektron és egy hozzátartozó neutrínó (vagy ezek antirészecskéi), ezért a 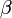 sugárzás részecskéjének az elektront tekintjük.
sugárzás részecskéjének az elektront tekintjük.
A gyengekölcsönhatással magyarázható, hogy ez a reakció lényegesen lassabban zajlanak le, mint az erős kölcsönhatással vezérelt beomlási reakciók (ilyenekkel a részecskefizika foglalkozik). Az alapvető folyamatok:
Negatív β-bomlás: 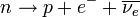
Pozitív β-bomlás: 
Ezek a folyamatokat az úgynevezett Feynman-gráfokkal érdemes jellemzni, például a negatív β-bomlás gráfja ilyen. A gráf csúcsaiban érvényes a lepton- és barionszám megmaradás. A fenti folyamatok átrendezésével további két reakció kapható:
Pozitronbefogás: 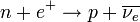
Elektronbefogás: 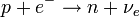
Ezek közül a felső gyakrolatilag nem játszódik le, mert az elektronburokban a pozitron annihilálódik, így nem tud eljutni a neutronig. Ezzel szemben az elektronok az atommag körül igen hosszú időt eltöltenek, és mivel a hullámfüggvényük szétfolyt, bizonyos valószínűséggel a mag helyén is tartózkodnak, így előfordulhat, hogy a magbeli proton befog egy elektront és átalakul.
Egyéb gyenge kölcsönhatás által vezérelt folyamatok:
A proton-proton lánc kezdőreakciója: 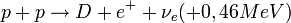
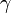 -bomlás
-bomlás
Ez a szerkezeti változással nemjáró folylamat a magbelső gerjesztettségét sugározza ki egy foton formájában. Ez a foton igen nagy energiájú is lehet, ezért számottevő biológisi veszélyt is hordoz.
Radioaktív családok
A nehéz atommagok könnyen bomlanak, azonban ekkor is csak aránylag kis csökkenés zajlik le bennük a rendszámban, következésképpen a belőlük kialakuló új mag is hajlamos bomlásra. Ezeket a láncokat nevezzük radioaktív családoknak. Az atommagok tömegét csak az alfabomlás csökkenti, mégpedig néggyel, ebből az következik, hogy a bomló magok négy csoportba sorolhatóak be az alapján, hogy 4-nek melyik maradékosztályába tartoznak. Ezt a négy csaoportot a négy radioaktív családnak nevezzük. Közülük a Neptúnium-család lényegében teljesen elbomlott a kezdő atommag rövid felezési ideje miatt, a másik három a Tórium, Rádium és Aktínium család még jelen van a Földön. A bomlási sorok stabil elemekben végződnek: a hérom hosszú család Ólomban, a Neptúnium család Talliumban végződik.
Elemi részecskék
Definíció szeirnt elemi részecskének nevezzük azokat az alkotókat, amelyeknek nem tulajdonítunk belső struktúrát. Jelenlegi ismereteink szerint ilyenek a kvarkok (u, d, c, s, t, b) és a leptonok (elektron, müon, tau, és a hozzájuk tartozó neutrínók). Ezeket generációkba rendezve csoportosíthatjuk, az elsőbe az u, d kvarkok, az elektron és az elektron neutrínó tartozik, a másodikba a c, s, müon és neutrínója, stb.
Alapvető kölcsönhatások
A természetben jelenlegi ismereteink szerint négy alapvető kölcsönhatás van. Ezek töltések között hatnak, és közvetítő részecskéket tudunk hozzájuk rendelni, ennek tömege alapján pedig -jelenlegi elméleteink szerint- kölcsönhatási távolságot.
- Elektromágneses kölcsönhatás: közvetítője a foton, nulla tömegű, ennélfogva végtelen a hatótávolsága, az elektormos töltések között hat, amelyekből két féle van, az azonosak vonzzák, a különbözőek taszítják egymást.
- Gavitációs: a közvetítő részecskéjét (gravitron) nem sikerült kimutatni, ennek ellenére a kísérleti tapasztalatok alapján végtelen hatótávolságot tulajdonítunk neki. A tömegek között hat, csak vonzó lehet. Nagyskálán határozza meg az univerzum viselkedését, mert a többi kölcsönhatás vagy kiátlagolódik, vagy túl gyorsan lecseng.
- Erős kölcsönhatás: a színtöltések között hat, közvetítői a gluonok, rövidhatótávolságú, ugyanakkor fajlagosan a legerősebb kölcsönhatás. Másodlagos kölcsönhatásként az atommagot tartja össze.
- Gyengekölcsönhatás: az ízek között hat, közvetítőrészecskéi a
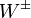 és
és 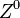 bozonok, amelyek nagy tömegűek, ezért a hatótávolság igen rövid. A radioaktivitásban és más lassú bomlásokban játszik szerepet.
bozonok, amelyek nagy tömegűek, ezért a hatótávolság igen rövid. A radioaktivitásban és más lassú bomlásokban játszik szerepet.
Kísérleti eszközök
A detektorok két típusát különböztetjük meg:
- számlálók - csak jelzik egy-egy részecske felbukkanását
- részecskenyom-detektorok - a detektoron áthaladó részecske pályáját rögzítik.
A detektálás során a részecske (sugárzás) és a detektoranyag valamilyen (általában EM) kölcsönhatását figyeljük meg. Semleges részecskék detektálása általában közvetett módon történik.
Gáztöltésű számlálók
Ionizációs kamra - felépítés: gázszigetelésű síkkondenzátor. Töltött részecske áthaladása esetén a gáz ionizálódik, a töltött részecskék a kondenzátorra kapcsolt feszültség (V) hatására mozogni fognak, az áram mérhető. Kis V esetén a töltéshordozók lassan mozognak, a rekombináció esélye nagy, ezért nem mindegyik jut el az elektródáig. Az áramerősség eleve kicsi, a kamra nagy intenzitások esetén használható (doziméter, kozmikus sugárzási mérések)
Proporcionális számláló - felépítés: cső alakú katód, benne középen egy anódszál, valamint a kettő között valamilyen gáz. Megfelelően nagy térerősség mellett egy szabadelektron két ütközés között a gáz ionizációs potenciáljának megfelelő energiára tehet szert, a gázmolekulával való ütközés után pedig már két elektron megy tovább. A folyamat többször megismétlődik, elektronlavina alakul ki. A végső jel arányos lesz a primer elektronok számával. Töltőgáznak metánt szoktak alkalmazni, mivel nagy az abszorpciója az ultraibolya tartományban (rekombinációkor ilyen energiájú fotonok sugárzódnak ki). Felhasználás: neutronfluxus mérése (bór-tetrafluorid töltőgáz, bór + neutron magreakció).
Proporcionális kamra - felépítés: a katód két síklemez, közötte anódszálak, közös gáztérben, a széleken vékony műanyagfóliával határolva. Megfelelő mennyiségű anódszál esetén a részecske áthaladásának helyét akár mm pontossággal is megkaphatjuk.
Driftkamra - mint a proporcionális kamra, csak a szálak közötti távolság nagyobb (~10 cm). Egy kiegészítő szcintillációs számláló használatával mérhető a részecske azon történő áthaladása és az anódszálon megjelenése közötti idő. Ha az áthaladás mentén a térerő teljesen homogén, a megtett út és az ehhez szükséges idő közötti összefüggés lineáris. Mágneses térben nem alkalmazható (elrontaná a homogén teret). Bonyolultabb konstrukció, mint a proporcionális kamra, de mivel kevesebb szál van benne, ezért az ehhez szükséges elektronika jóval kevesebb (és olcsóbb).
Geiger-Müller cső - proporcionális számláló, magasabb tápfeszültségen. Egy elektron által megindított kisülés önfenntartó, így a jel detektálása egyszerűbb. Energiamérésre nem alkalmas. Argon + alkohol töltőgázkeverék alkalmazásával elérhető, hogy a számláló önkioltó legyen.
Szikrakamra - proporcionális kamra-szerűség. A síklap és a szálak között elegendő nagy feszültség esetén a kettő között szikra ütne át. Ha ennél a feszültségnél valamivel kisebbet kapcsolunk a vezetőkre, akkor egy, a detektoron áthaladó ionizáló részecske nyomán a szikra kialakulásának valószínűsége nagy lesz. Egy korábbi részecske által létrehozott ionokat egy álandó, nagyságrendileg 100 V-os tértisztító feszültséggel tüntetjük el. Koordináta-detektorként használható, az egyes szálak melletti elhaladás rögzíthető elektronikusan, vagy a szikrasorozat lefényképezésével.
Szcintillációs számlálók
A kristályokban keletkező felvillanásokat detektáljuk. Eleinte az észlelés szabad szemmel történt, később fotoelektron-sokszorozót alkalmaztak.
Felépítése:
- szcintillátor - a sugárzás itt alakul át fényenergiává,
- fotoelektron-sokszorozó - fényfelvillanás elektromos impulzussá alakítása,
- erősítés, analizálás, regisztrálás elektronikusan.
Töltött részecskék és fotonok detektálására alkalmas, utóbbi másodlagos folyamatok által (fotoeffektus, Compton-szórás, párkeltés). Gyakran használt szcintillátorok: ZnS(Cu), NaI(Tl), CsI(Tl), naftalin kristályok, toluol (folyadék).
Félvezető detektorok
Elsősorban Si, Ge használata, Li-al szennyezve vagy nagyon tiszta formában. Ge csak nagyon alacsony hőmérsékleten használható, viszont mivel nagyobb a rendszáma, mint a szilíciumé, előnyösebb a gamma-sugárzások detektálásához.
A félvezető detektorokban egységnyi átadott energia hatására lényegesen több töltéshordozó keletkezik, mint a szcintillációs vagy a gázionizációs detektorokban. Az ingadozás kisebb, ezért a felbontóképesség jobb.
Részecskenyom-detektorok
Elsősorban töltött részecskék detektálására alkalmas szerkezetek, ugyanis ezek azok, amelyek nyomot hagynak maguk után.
(Wilson-féle) ködkamra - túltelített gáz-gőz keverék. Ionizáló részecske nyomán a gázionokon a gőzcseppek kicsapódnak, láthatóvá válnak. Rözgzítés: lefényképezzük. Kiegészíthető számláló detektorokkal, így a felvétel készítése vezérelhető.
Buborékkamra - forráspont fölé túlfűtött folyadékban a töltött részecske áthaladása után keletkezett ionpárok buborékokat hoznak létre. Ha a folyadék nyomását hirtelen lecsökkentjük, a pálya mentén lefényképezhető méretű buborékok (~ 200 mikrométer) alakulnak ki. Nagy méretű, költséges szerkezetek.
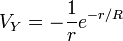
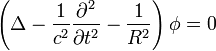
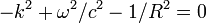
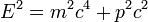
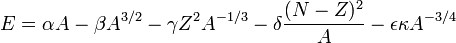
![- \frac{dE}{dx} = \frac{4 \pi nZ^2}{m_e v^2} \cdot \left(\frac{e^2}{4\pi\epsilon_0}\right)^2\cdot \left[\ln \left(\frac{2m_e v^2 }{I}\right)\right]](/images/math/b/a/7/ba7c7b45842bc74cb7991ca32b168d01.png)