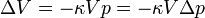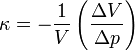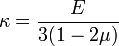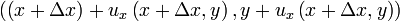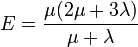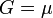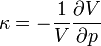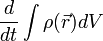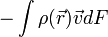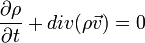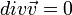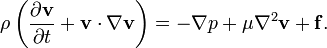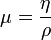Folytonos közegek mechanikája
Tartalomjegyzék
Rugalmas és képlékeny alakváltozások
Nyújtás
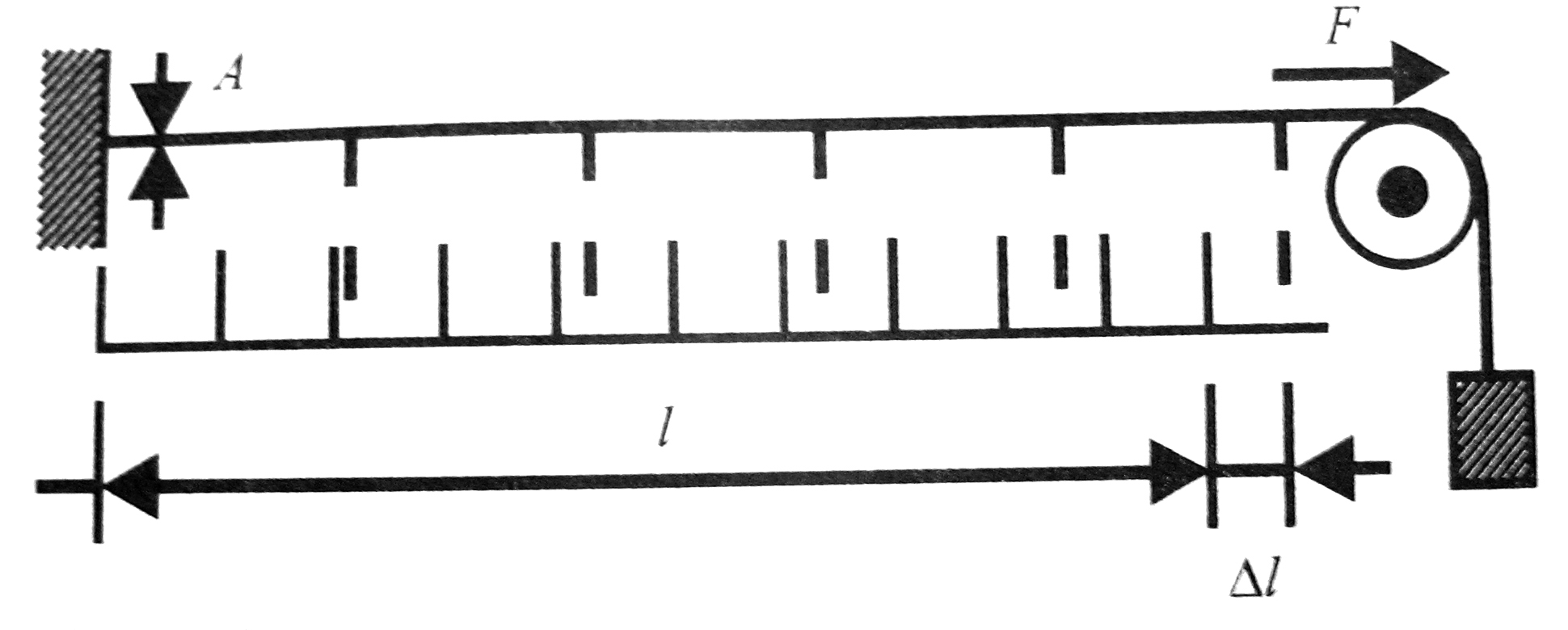
Ha egy homogén, A keresztmetszetű, l hosszúságú huzalt terhelünk megfelelően (nem túl) kicsi F erővel, akkor a megnyúlásra a következő arányosság (illetve egyenlőség) fog teljesülni:
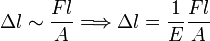 ,
,
ahol E a Young-modulus [nyomás dimenziójú]. Ez utóbbi nem más, mint a nyúlásra vonatkozó Hooke-törvény. Bevezetve a relatív hosszváltozást 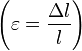 és a (mechanikai) feszültséget
és a (mechanikai) feszültséget 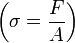 , a Hooke-törvény a következőképp alakul:
, a Hooke-törvény a következőképp alakul:
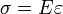
Ez az összefüggés már lokális törvény (tetszőleges keresztmetszetre igaz). Mivel  teljes hosszon egyenletes, ezért homogén deformációról beszélünk. Ellenkező esetben inhomogén deformációról van szó (pl.: saját súlyával terhelt rúd megnyúlása).
teljes hosszon egyenletes, ezért homogén deformációról beszélünk. Ellenkező esetben inhomogén deformációról van szó (pl.: saját súlyával terhelt rúd megnyúlása).
Munka és energiasűrűség nyújtás közben:
Ha 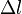 -lel megnyújtunk egy l hosszúságú rudat, akkor nyújtás közben x megnyújtásnál
-lel megnyújtunk egy l hosszúságú rudat, akkor nyújtás közben x megnyújtásnál 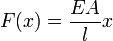 erő ébred a rúdban. Így a lineárisan növekvő erő összes munkája (összevetve a rugóerővel):
erő ébred a rúdban. Így a lineárisan növekvő erő összes munkája (összevetve a rugóerővel):
![E_{r}=W=\int_{0}^{\Delta l}F(x)dx=\frac{EA}{l}\int_{0}^{\Delta l}xdx=D\left[\frac{x^{2}}{2}\right]_{0}^{\Delta l}=\frac{1}{2}D(\Delta l)^{2}](/images/math/4/3/0/43080d474c3395108689e95af9107c2f.png) ,
,
ahol D a huzal direkciós állandója. Mivel homogén deformációról van szó, ezért alkalmazhatjuk a következő felírást az energia sűrűségre:
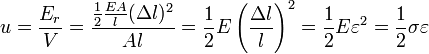
Nyújtást kísérő harántösszehúzódás:
Kísérletek alapján nyújtás során a harántmérték relatív változása 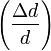 egyenesen arányos a hosszméret relatív változásával
egyenesen arányos a hosszméret relatív változásával 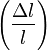 :
:
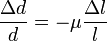 és
és 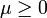 ,
,
ahol 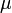 a Poisson-szám. Tehát nyújtáskor harántösszehúzódás, összenyomáskor haránt irányú méretnövekedés lesz. Ennek következtében a rúd térfogata megváltozhat. Tapasztalat szerint az anyagok térfogata nyújtáskor általában nem csökken, tehát
a Poisson-szám. Tehát nyújtáskor harántösszehúzódás, összenyomáskor haránt irányú méretnövekedés lesz. Ennek következtében a rúd térfogata megváltozhat. Tapasztalat szerint az anyagok térfogata nyújtáskor általában nem csökken, tehát
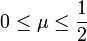 .
.
Speciális anyagú testek térfogata nőhet is, ekkor a Poisson-szám negatív.
Térfogati összenyomás
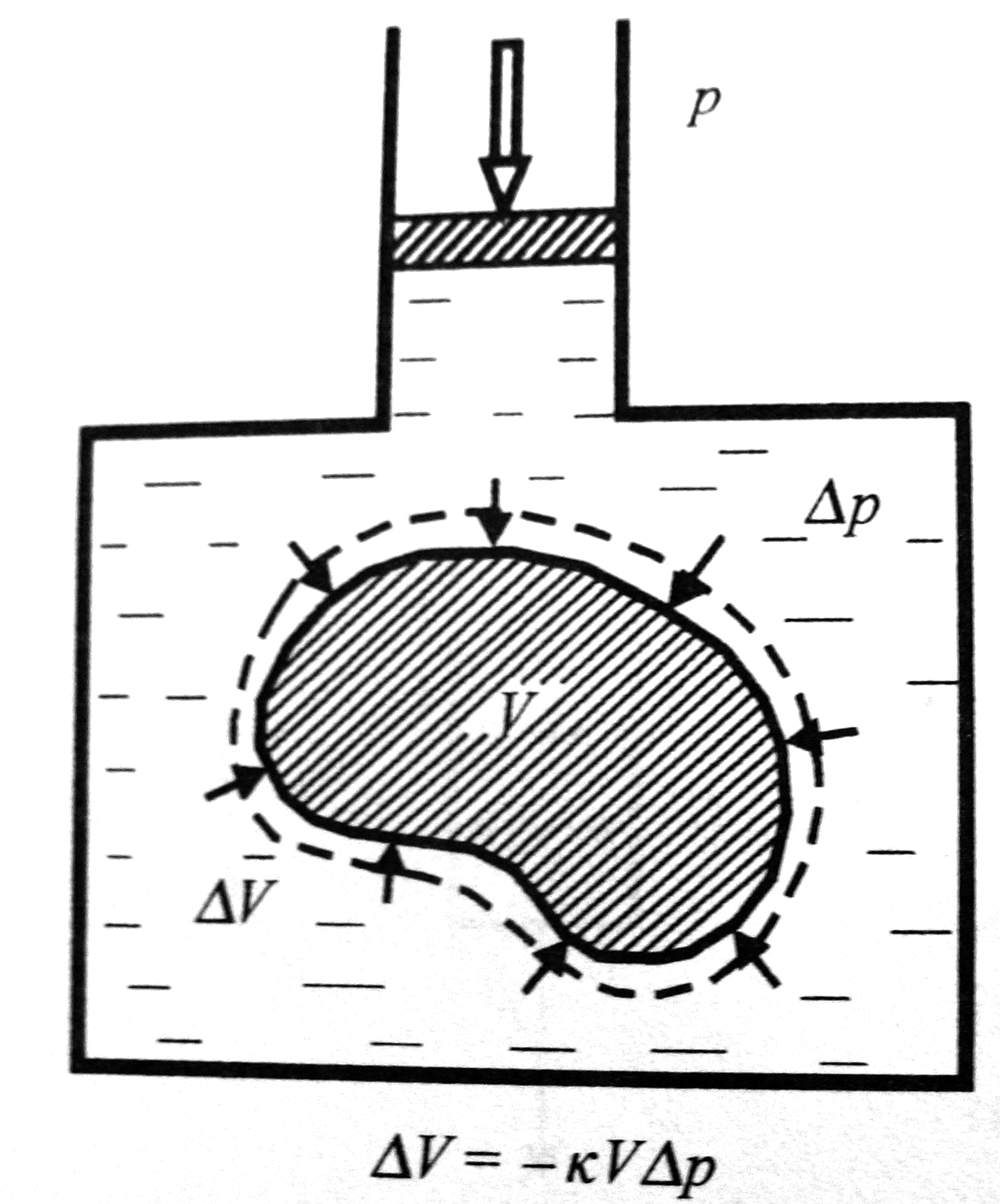
A test felületén egységesen eloszló térfogati összenyomást úgy valósíthatunk meg, ha például folyadékba tesszük, és úgy fejtünk ki a rendszerre nyomást:
Tapasztalat szerint a térfogat csökkenés arányos a test térfogatával és a testre gyakorolt nyomással/nyomás változással:
ahonnan:
az anyag kompresszibilitása. Ez utóbbi megadja, mekkora a relatív térfogat csökkenés egységnyi nyomásnövekedés hatására. Ez összefüggésben van a fentebb bevezetett Young és Poisson számokkal:
Nyírás
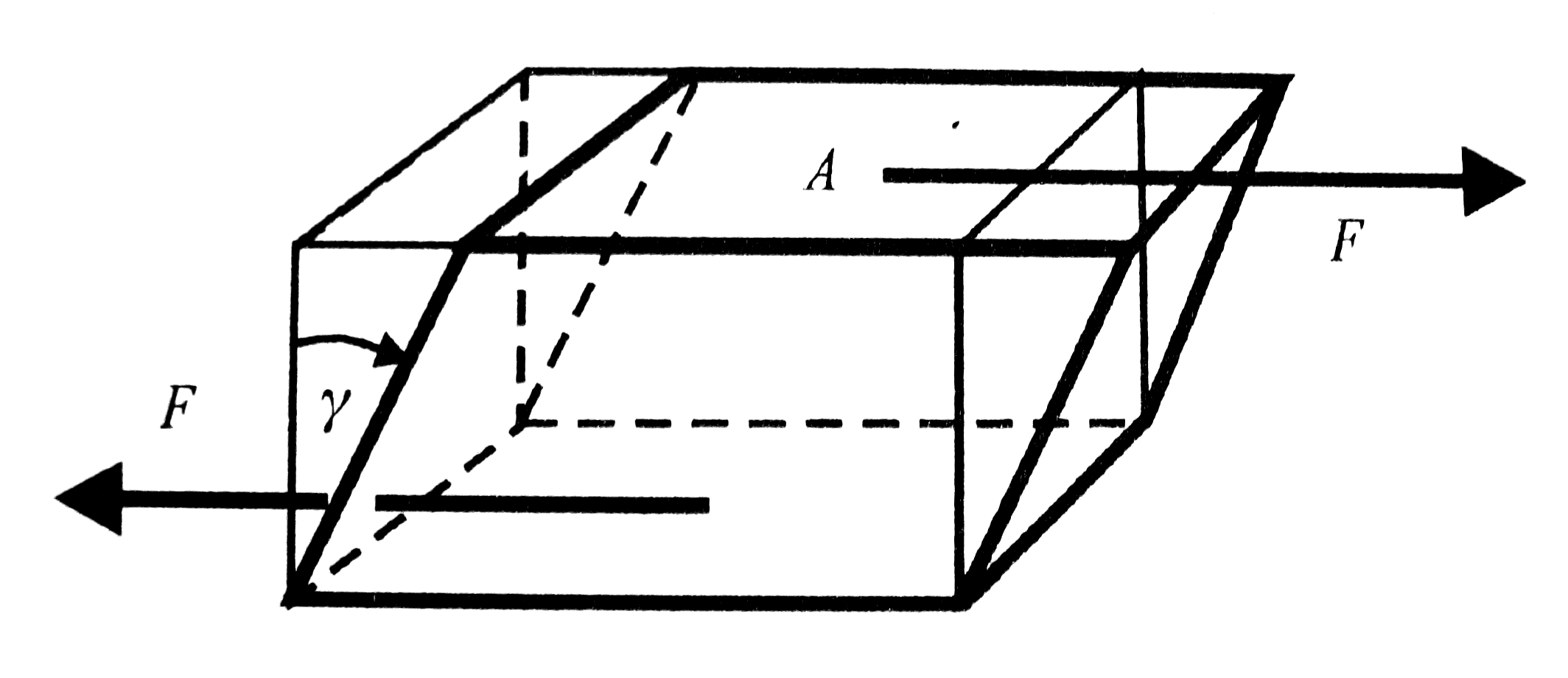
Ha egy rugalmas hasábra lapjával párhuzamosan erőt fejtünk ki, akkor a hasáb egy bizonyos 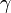 szöggel fog deformálódni. Ez a nyírás, és a szög (tapasztalatok szerint) megfelelően kis erő esetén arányos az erővel és fordítottan arányos a lap területével. Továbbá függ az anyagi minőségtől:
szöggel fog deformálódni. Ez a nyírás, és a szög (tapasztalatok szerint) megfelelően kis erő esetén arányos az erővel és fordítottan arányos a lap területével. Továbbá függ az anyagi minőségtől:
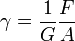 , ahol G az anyagi minőségtől függő nyírási modulus. Ha ez nagy érték, akkor az anyag erősen ellenálló a nyíró erőknek.
, ahol G az anyagi minőségtől függő nyírási modulus. Ha ez nagy érték, akkor az anyag erősen ellenálló a nyíró erőknek.
Mindezt úgy értelmezhetjük, hogy külső F erő hatására az erővel párhuzamos rétegek elcsúsznak egymáson, így ennek megfelelően visszahúzó 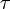 nyírófeszültség ébred. Az ebből származó erő kiegyenlíti a külső erőt:
nyírófeszültség ébred. Az ebből származó erő kiegyenlíti a külső erőt:
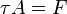 , azaz
, azaz 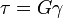 .
.
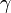 -t kifejezve a Hooke-törvénnyel analóg kifejezést kapunk. Mindkét egyenletnek a lényege, hogy a deformáció arányos a feszültséggel. A nyújtáshoz hasonlóan itt is bevezethető (és hasonlóan számolható is) a munka (W) valamint az energiasűrűség (u).
-t kifejezve a Hooke-törvénnyel analóg kifejezést kapunk. Mindkét egyenletnek a lényege, hogy a deformáció arányos a feszültséggel. A nyújtáshoz hasonlóan itt is bevezethető (és hasonlóan számolható is) a munka (W) valamint az energiasűrűség (u).
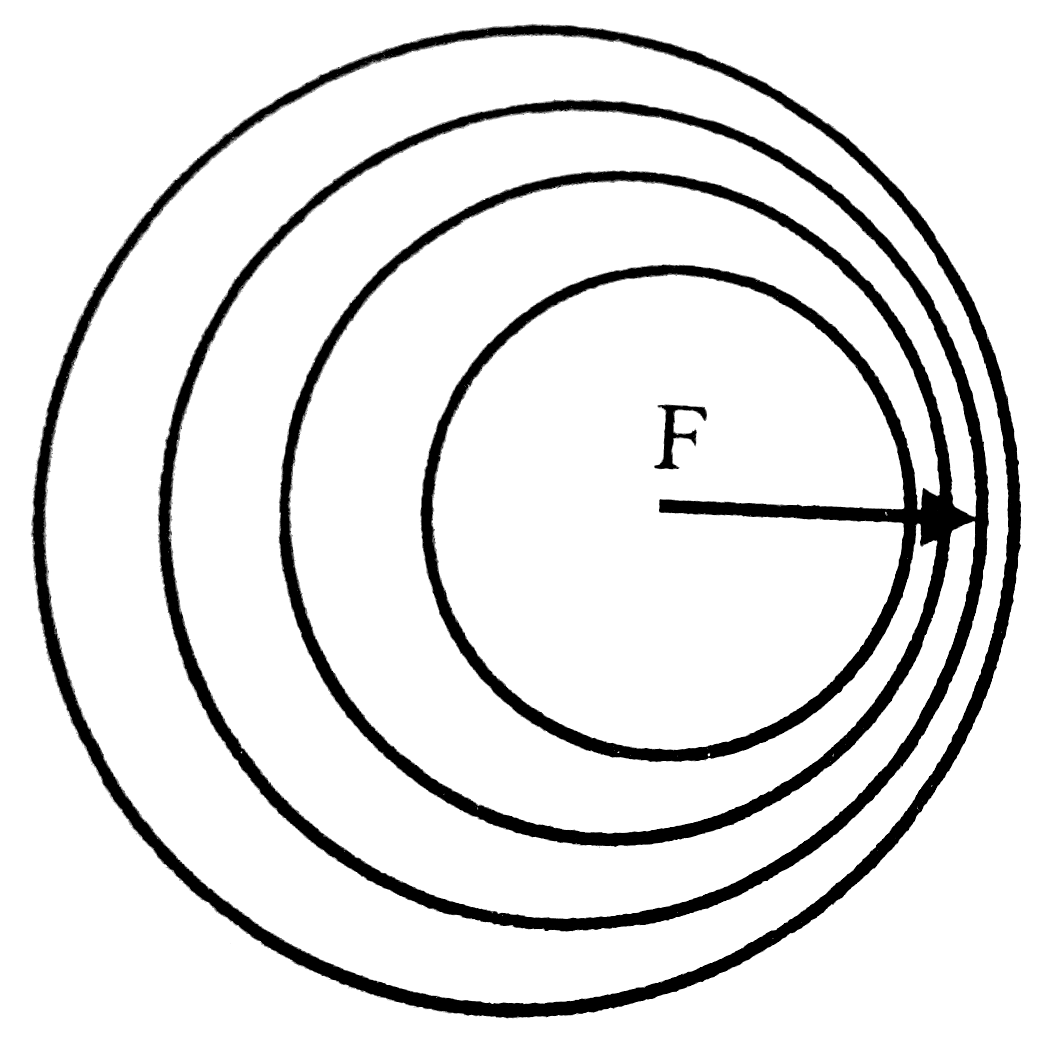
Csavarás
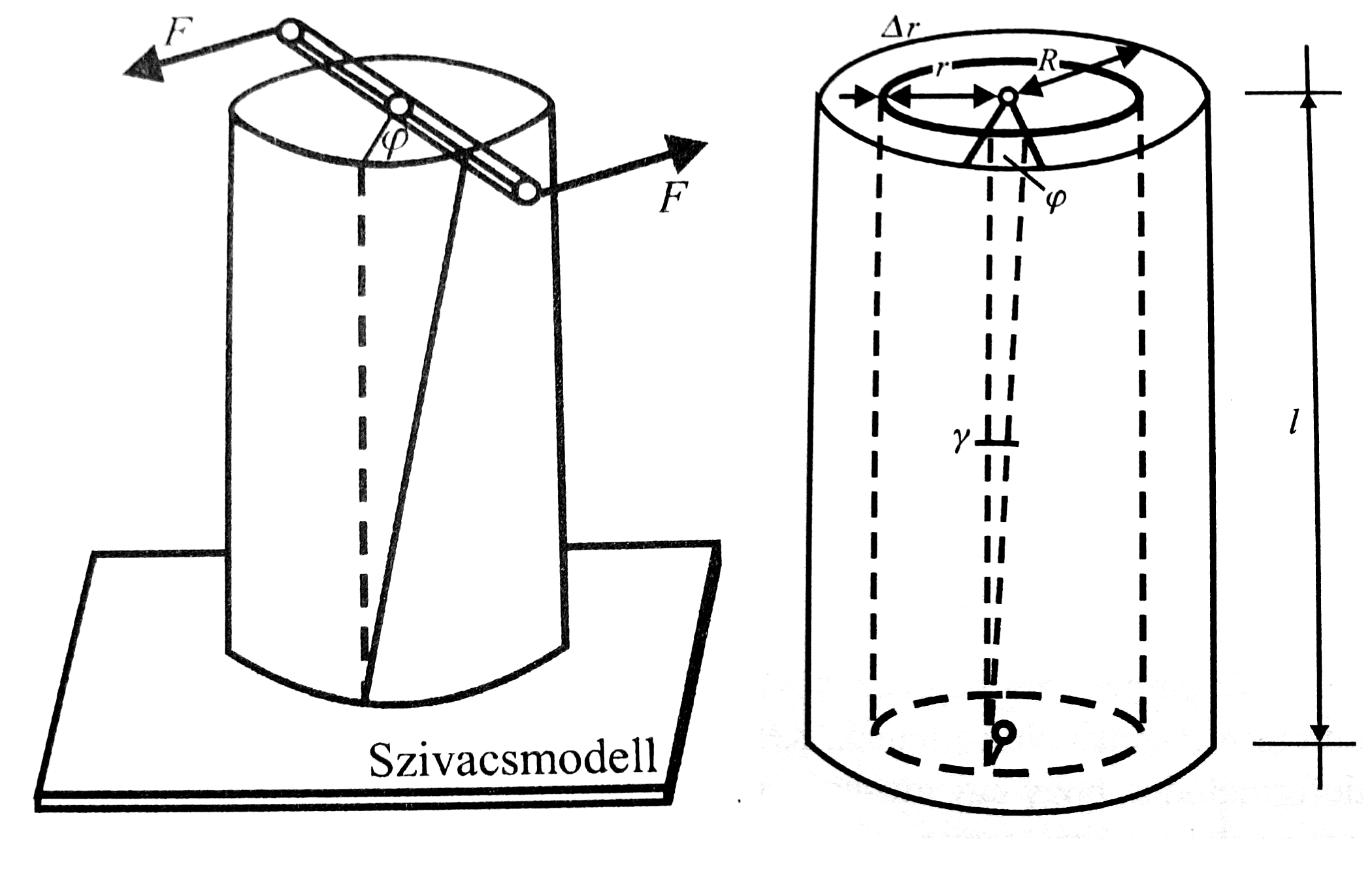
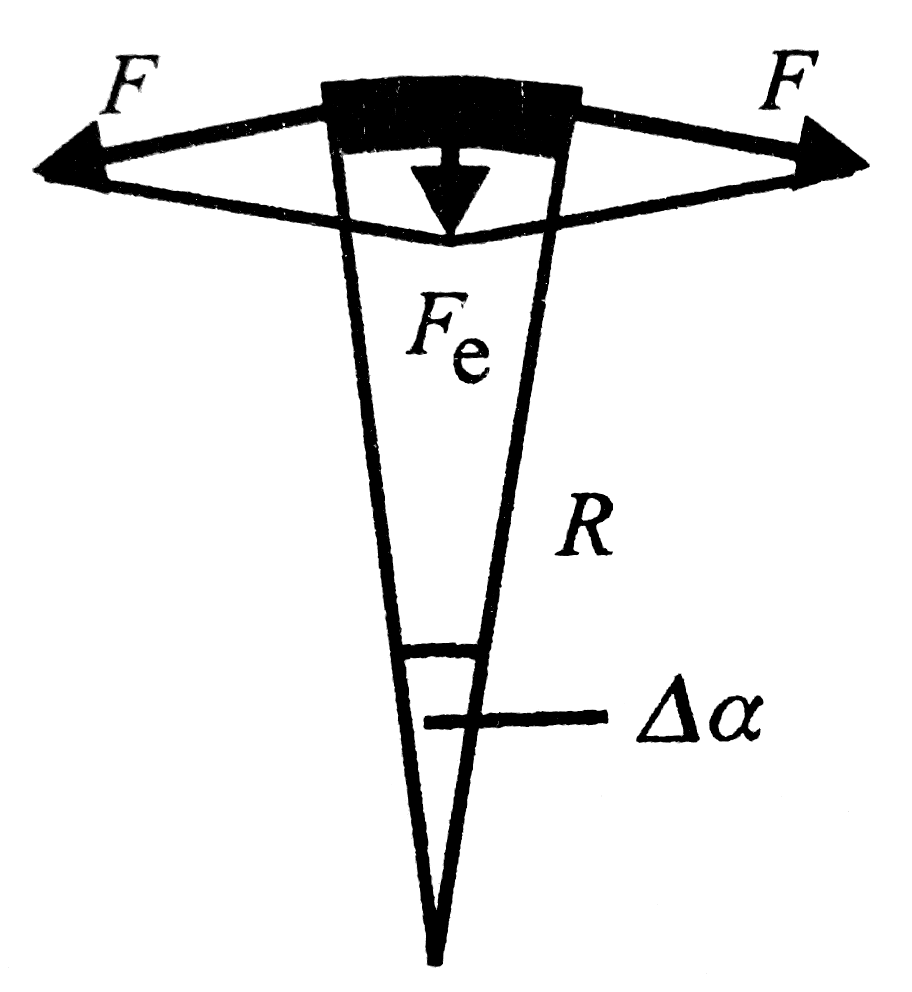
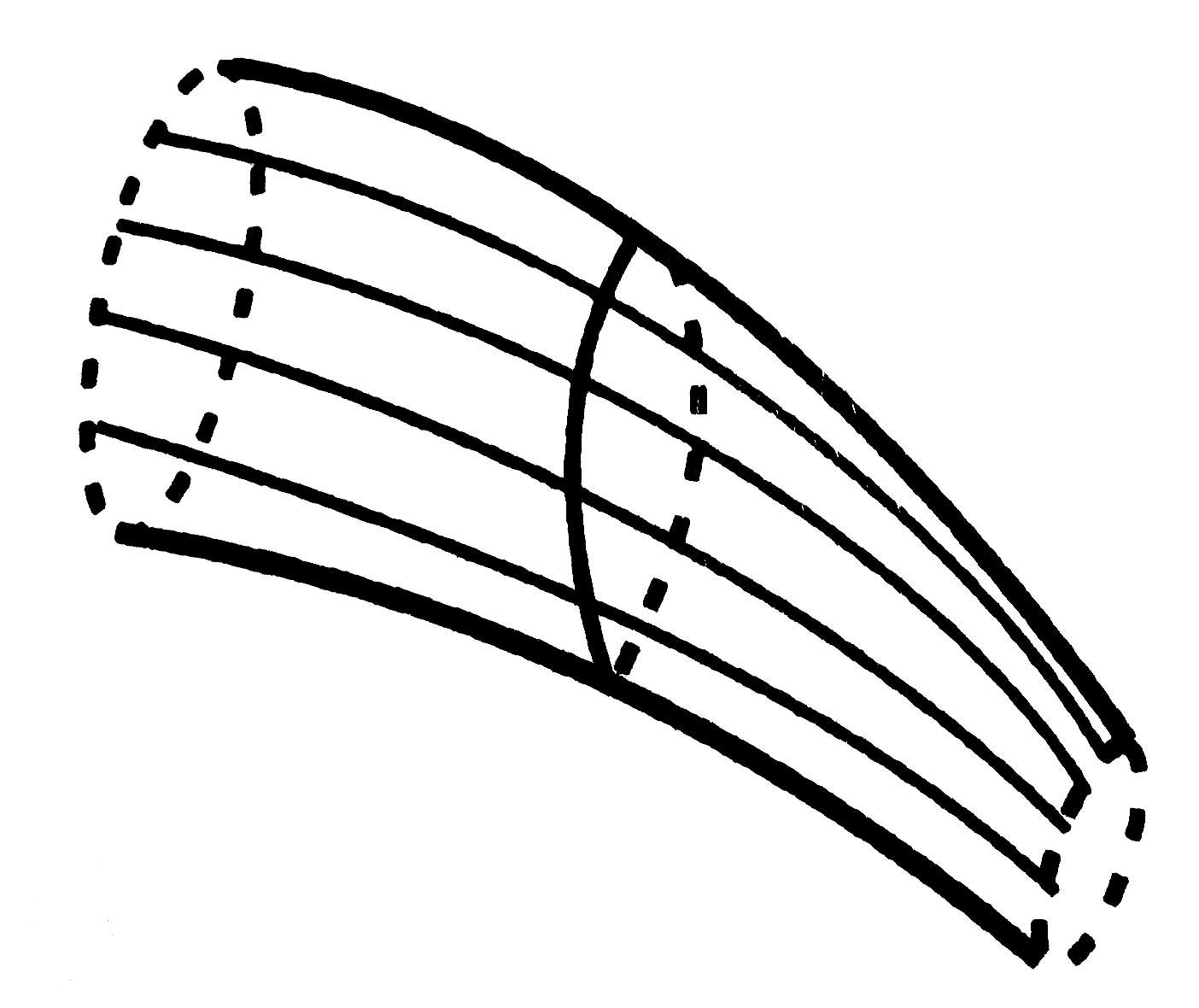
Az ábrákon látható módon deformáljuk a hengert, és a megértés érdekében felbontjuk koncentrikus hengerekre/csövekre (2. ábra).
Az r és 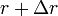 falvastagságú hengerek a csavarás során nyíródnak egymáson. (Tehát az eredetileg hasáb formájú palást paralelepipedonná torzul.) Így a deformációt leíró két szög között az összefüggés:
falvastagságú hengerek a csavarás során nyíródnak egymáson. (Tehát az eredetileg hasáb formájú palást paralelepipedonná torzul.) Így a deformációt leíró két szög között az összefüggés:
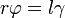
Tehát 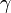 és így vele a deformáció mértéke is r-rel arányos. A fentiekből:
és így vele a deformáció mértéke is r-rel arányos. A fentiekből:
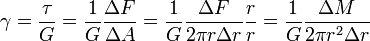 , ahol
, ahol 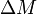 az erőnyomaték.
az erőnyomaték.
A nyomatékot kiszámítva (integrálva) a teljes hengerre, megadható az elcsavarodás szöge (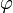 ), amiből azt kapjuk, hogy az elfordulás szöge egyenesen arányos a szabad végen ható forgatónyomatékkal és fordítottam arányos a sugár negyedik hatványával. Ez utóbbi tulajdonság miatt széleskörben alkalmaznak torziós mérlegeket.
), amiből azt kapjuk, hogy az elfordulás szöge egyenesen arányos a szabad végen ható forgatónyomatékkal és fordítottam arányos a sugár negyedik hatványával. Ez utóbbi tulajdonság miatt széleskörben alkalmaznak torziós mérlegeket.
Hajlítás
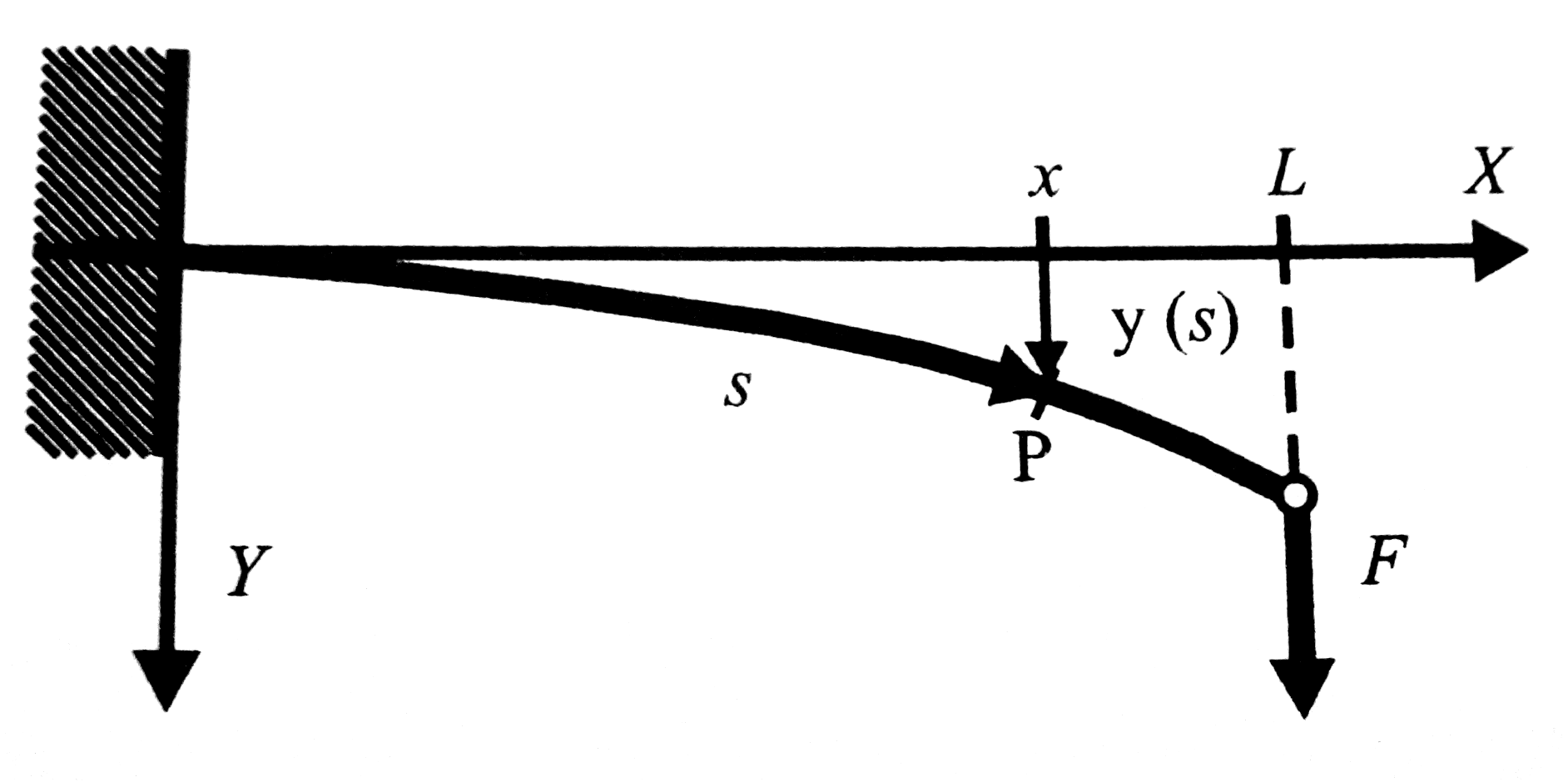
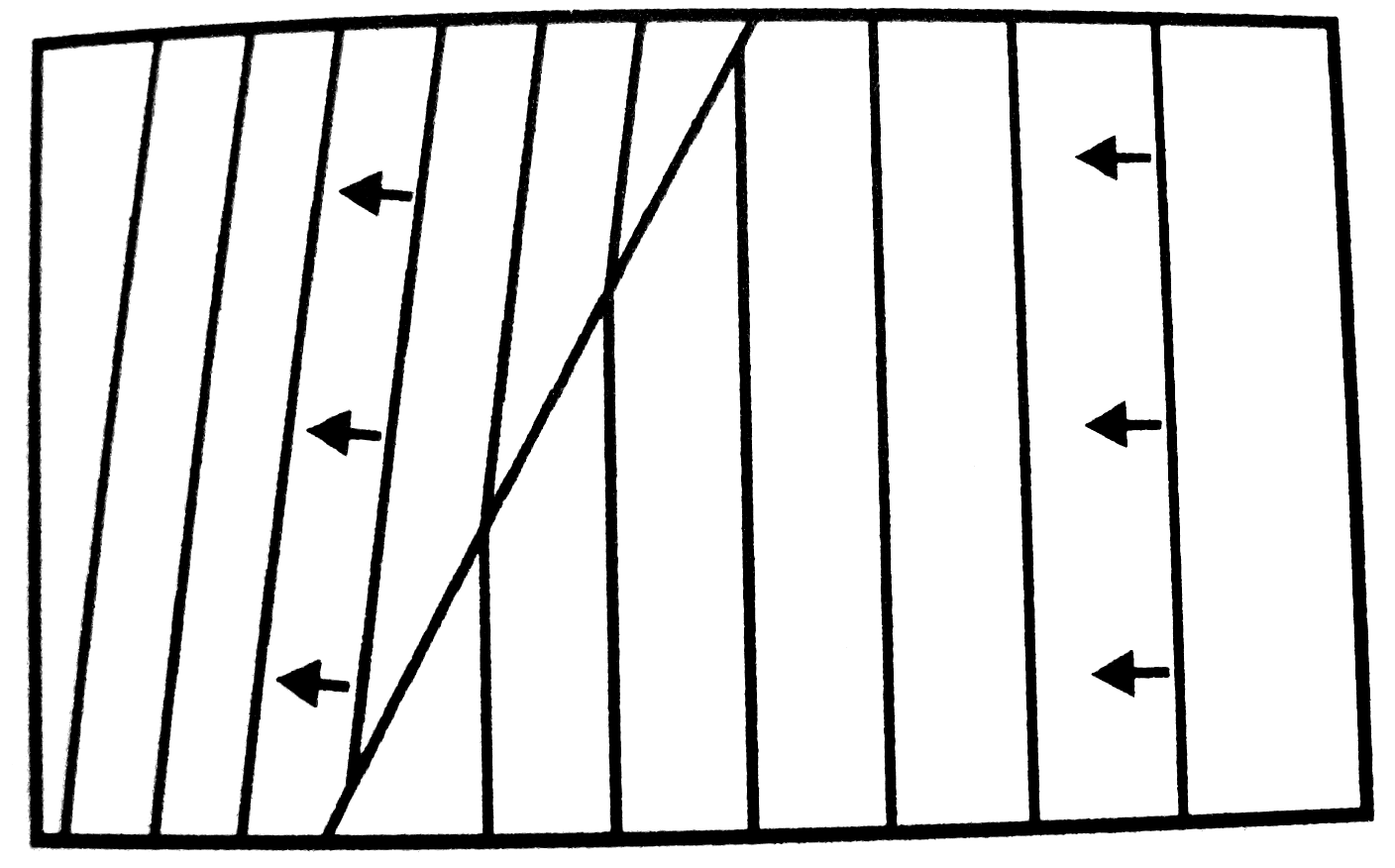
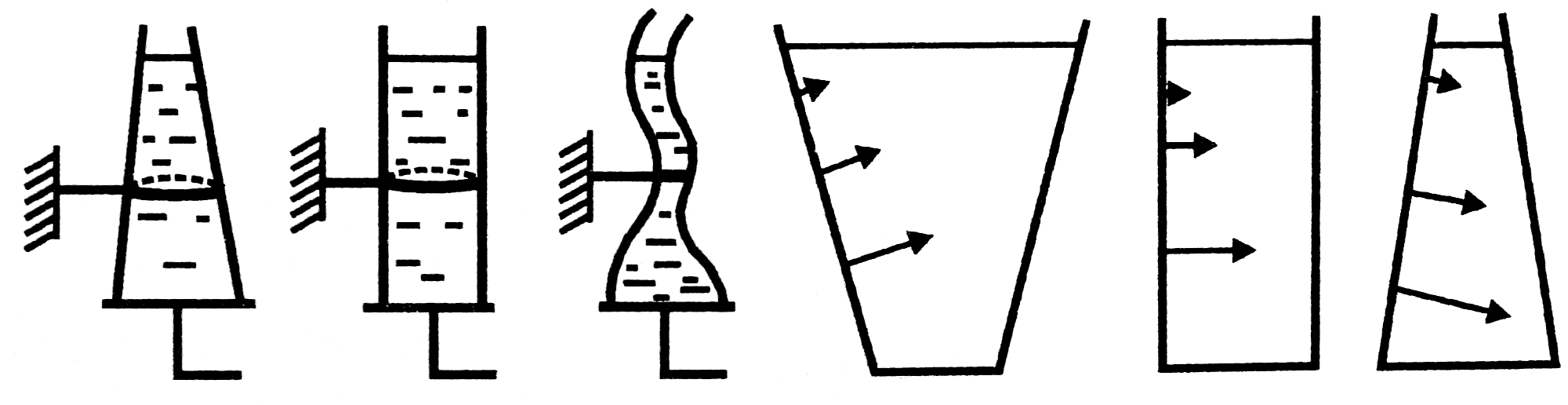
Rugalmas rúd hajlítása esetén a keresztmetszeti lapok mozdulnak el egymáshoz képest. Az egyes rúddarabok úgy deformálódnak, hogy egy réteg felett nyúlik, alatta pedig összenyomódik az anyag (ezek mértéke függ a köztes résztől való távolságtól). A köztes részt, melynek hossza nem változik, neutrális zónának nevezzük. Egyik jól használható példa, ha egy oldalán rögzített rúdnak a másik végére F erőt fejtünk ki, lásd az ábrát.
Továbbá eltekintünk a rúd hossztengelyére merőleges síkkeresztmetszetének torzulásától. Így feltételezhetjük, hogy mindig érvényes a Hooke-törvény (Ekkor a neutrális réteg egy neutrális görbe lesz csupán).
Mindezek alapján megadható mekkora erő ébred az egyes tartományokban, mekkora a Young-modulus, mekkora a belső feszültségek eredő forgatónyomatéka stb. További tipikus hajlítási módszerek:
Feszültség- és deformációs tenzor
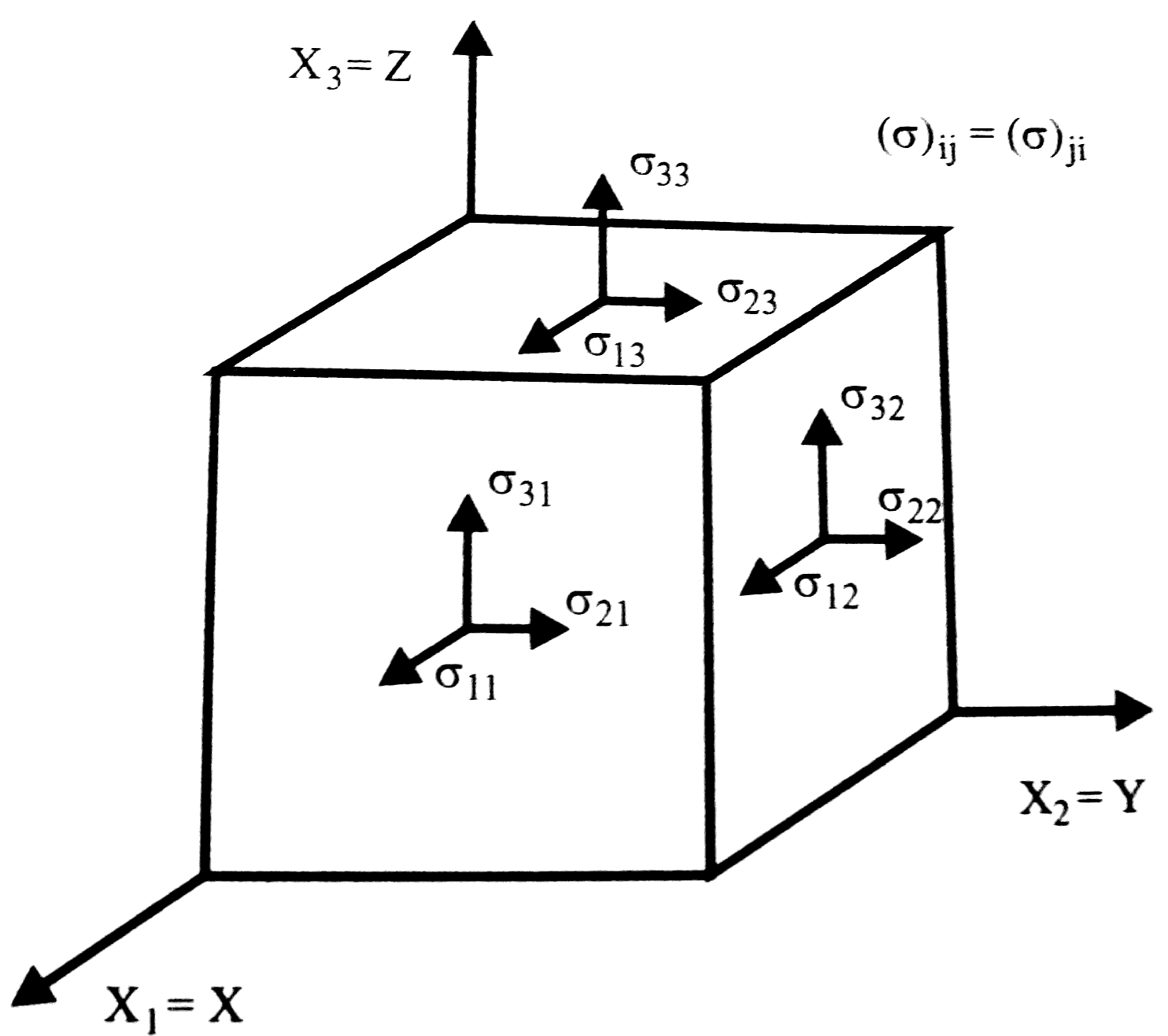
Feszültség tenzor felírása
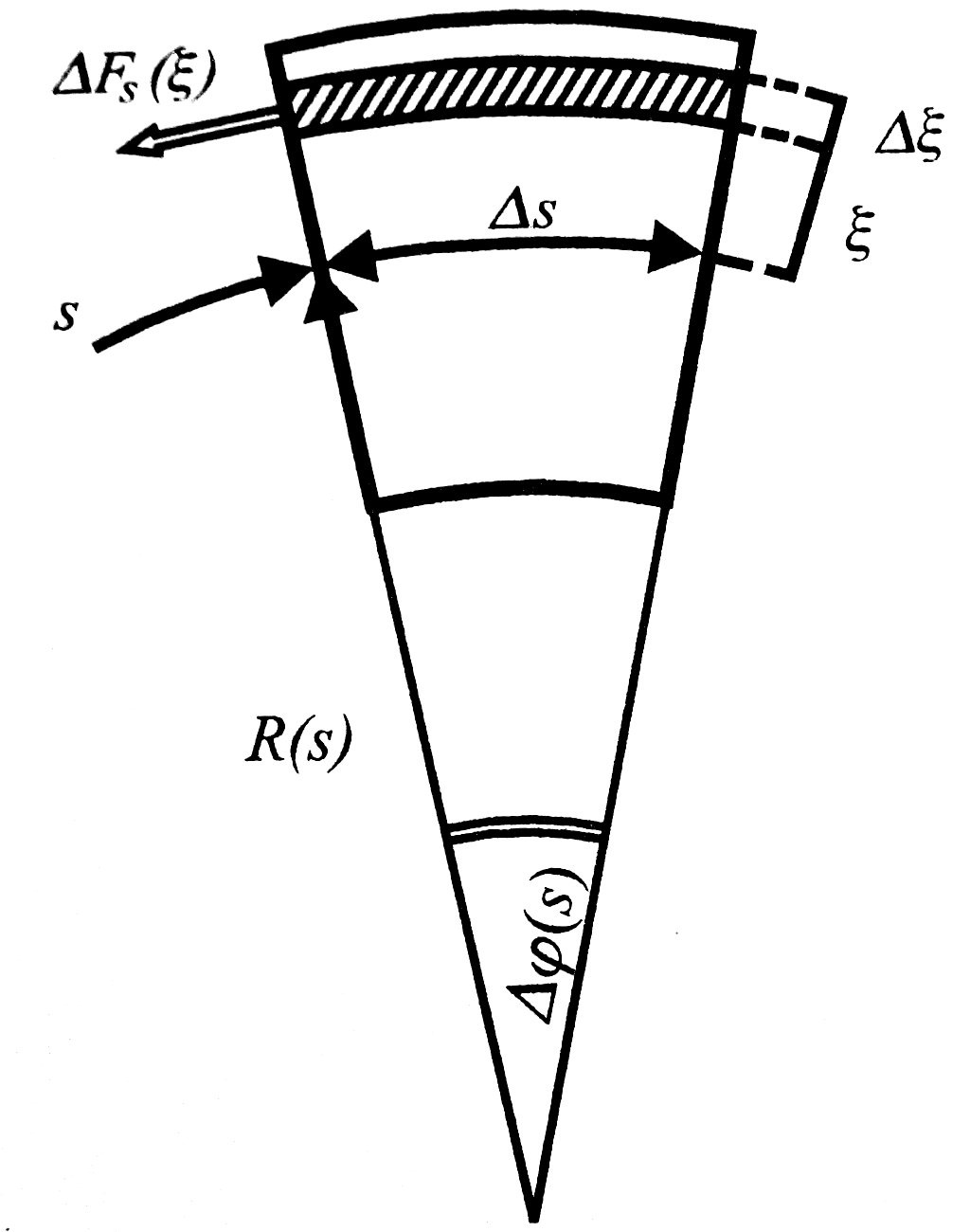
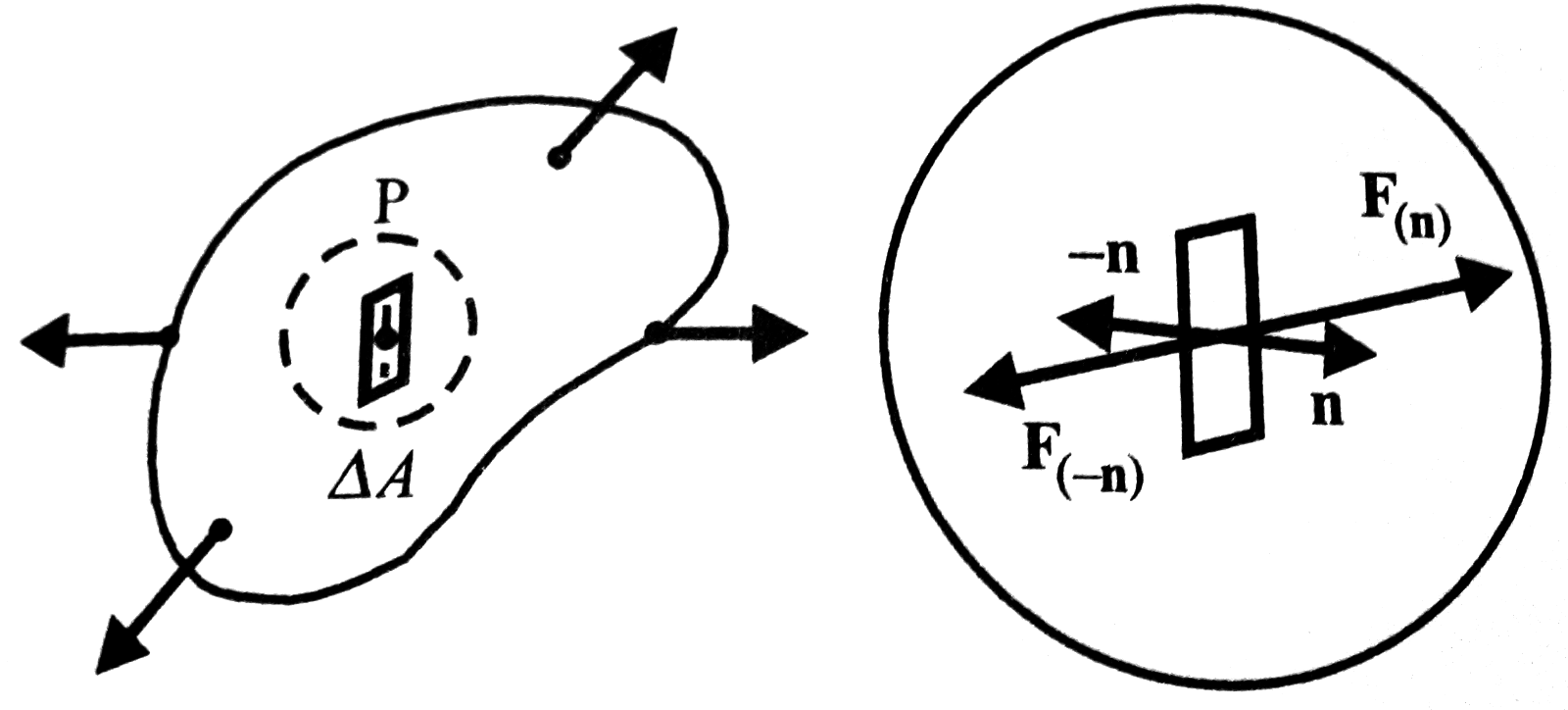
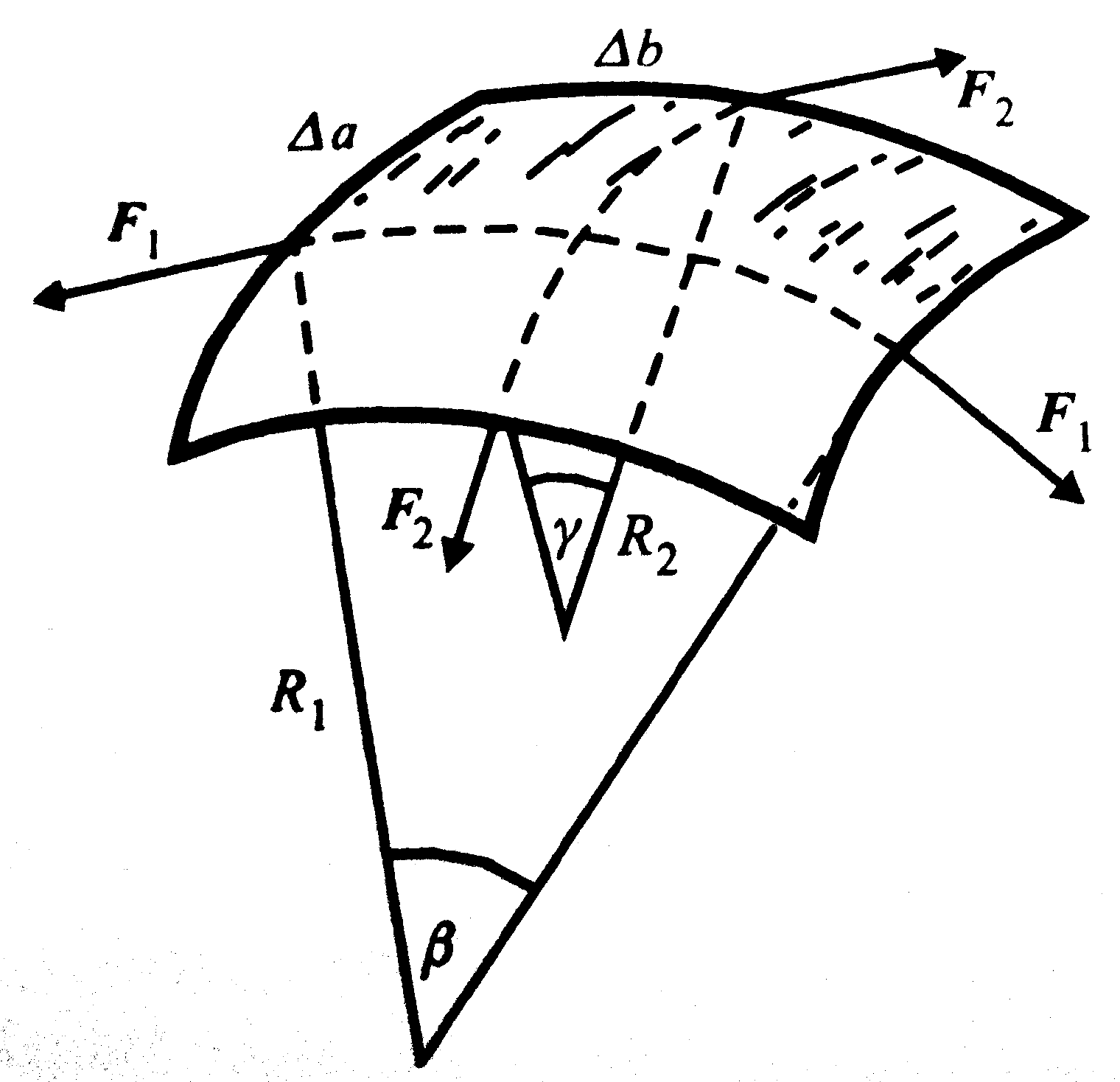
A pontos vizsgálat céljából vegyünk egy 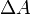 nagyságú felületelemet a testben, ami tartalmazza a P pontot. n a felületre merőleges normálvektorunk.
nagyságú felületelemet a testben, ami tartalmazza a P pontot. n a felületre merőleges normálvektorunk.
Ha szétvágjuk a testet 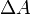 mentén, akkor ahhoz hogy újra összeillesszük, egy ugyanakkora, ellentétes irányú erőre lesz szükségünk. Tehát
mentén, akkor ahhoz hogy újra összeillesszük, egy ugyanakkora, ellentétes irányú erőre lesz szükségünk. Tehát
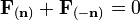
Bevezetve a feszültségvektort: 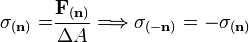
A feszültségek felületi erők, tehát egy adott felületen keresztül fejtik ki hatásukat. Továbbá belső erőkből származnak és rövid a hatótávolságuk. Valamint léteznek még térfogati erők, melyek tetszőleges 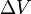 térfogatelemre hatnak:
térfogatelemre hatnak:
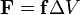 , ahol
, ahol 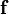 a térfogati erősűrűség (amely helyfüggő).
a térfogati erősűrűség (amely helyfüggő).
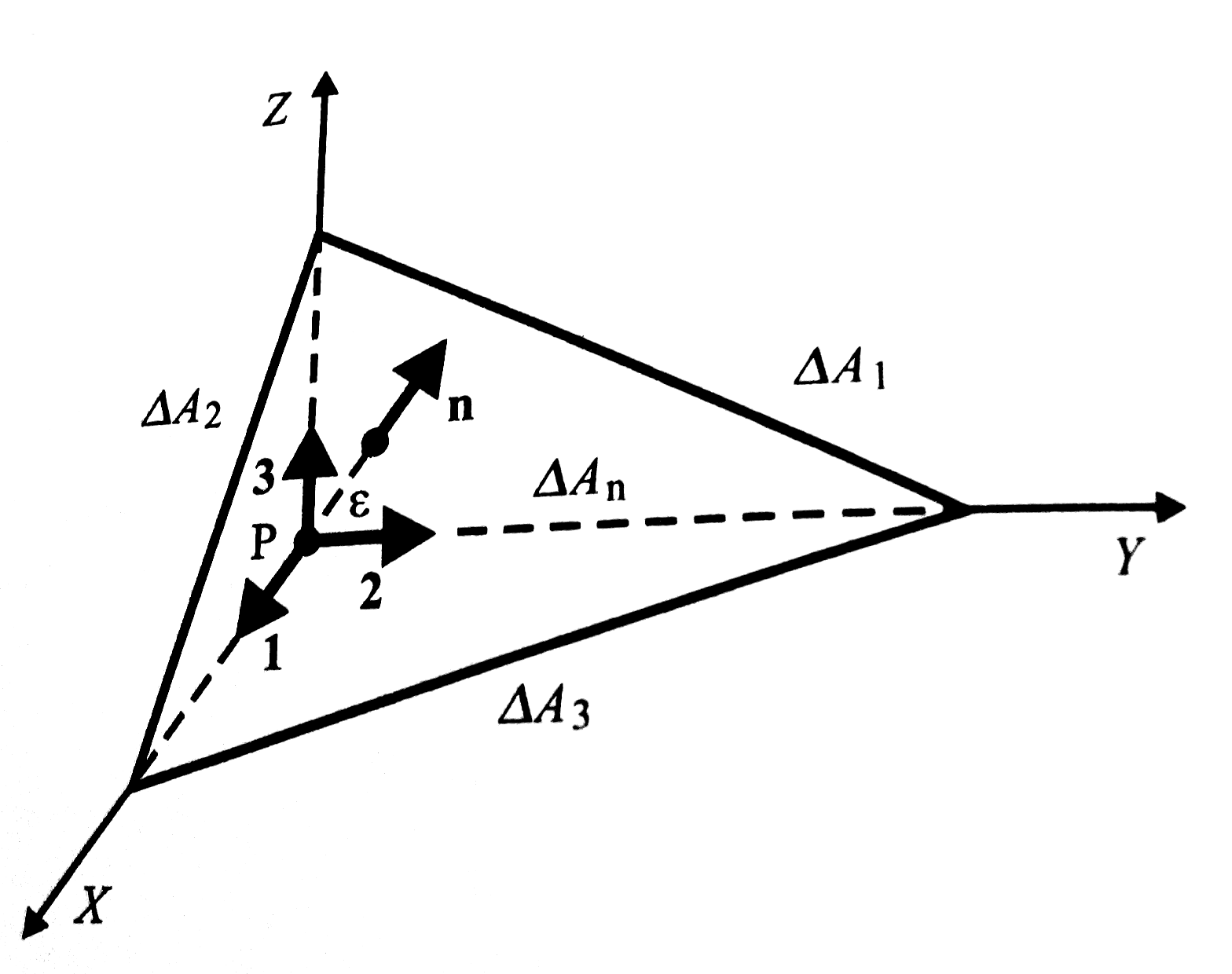
Ha a P pontban felveszünk egy X,Y,Z (1,2,3) irányú egyégvektorok által kifeszített tetraédert, akkor a következő ábrát kapjuk (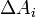 -k rendre az oldalak területei):
-k rendre az oldalak területei):
A térfogati erőkkel a 4 lapon működő feszültségekből származó erők tartanak egyensúlyt:
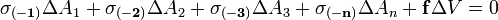
 (ábra fent) nem más, mint
(ábra fent) nem más, mint 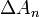 távolsága P ponttól, mellyel a térfogati erők nagyságrendje köbösen, a felületi erőké pedig négyzetesen változik. Ezért
távolsága P ponttól, mellyel a térfogati erők nagyságrendje köbösen, a felületi erőké pedig négyzetesen változik. Ezért  határesetben:
határesetben:
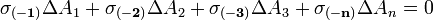
Mivel az egyes felületek kifejezhetők 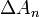 segítségével (
segítségével (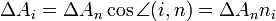 ), ezért az egyenlet a következőképp egyszerűsödik:
), ezért az egyenlet a következőképp egyszerűsödik:
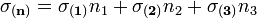
Tehát ha ismerjük a koordinátasíkokon fellépő feszültséget, akkor bármilyen n irányban meg tudjuk határozni a feszültséget:
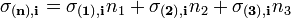 (i=1,2,3)
(i=1,2,3)
Így bevezethetjük a 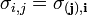 feszültség tenzort, amellyel a fenti egyenlet:
feszültség tenzort, amellyel a fenti egyenlet:
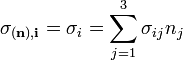
(Tenzorról akkor beszélünk, ha a mátrix homogén, lineáris vektortranszformációban szerepel.) A feszültség tenzor j-edik oszlopában a feszültség komponensek állnak. A főátló komponensei a nyújtási/összenyomási feszültségek, a többi elem pedig nyírási feszültség. Továbbá bizonyítható, hogy a feszültségtenzor szimmetrikus[1].
Deformációs tenzor felírása
Síkbeli deformációt vizsgálva (amit később kiterjesztünk 3D-ra):
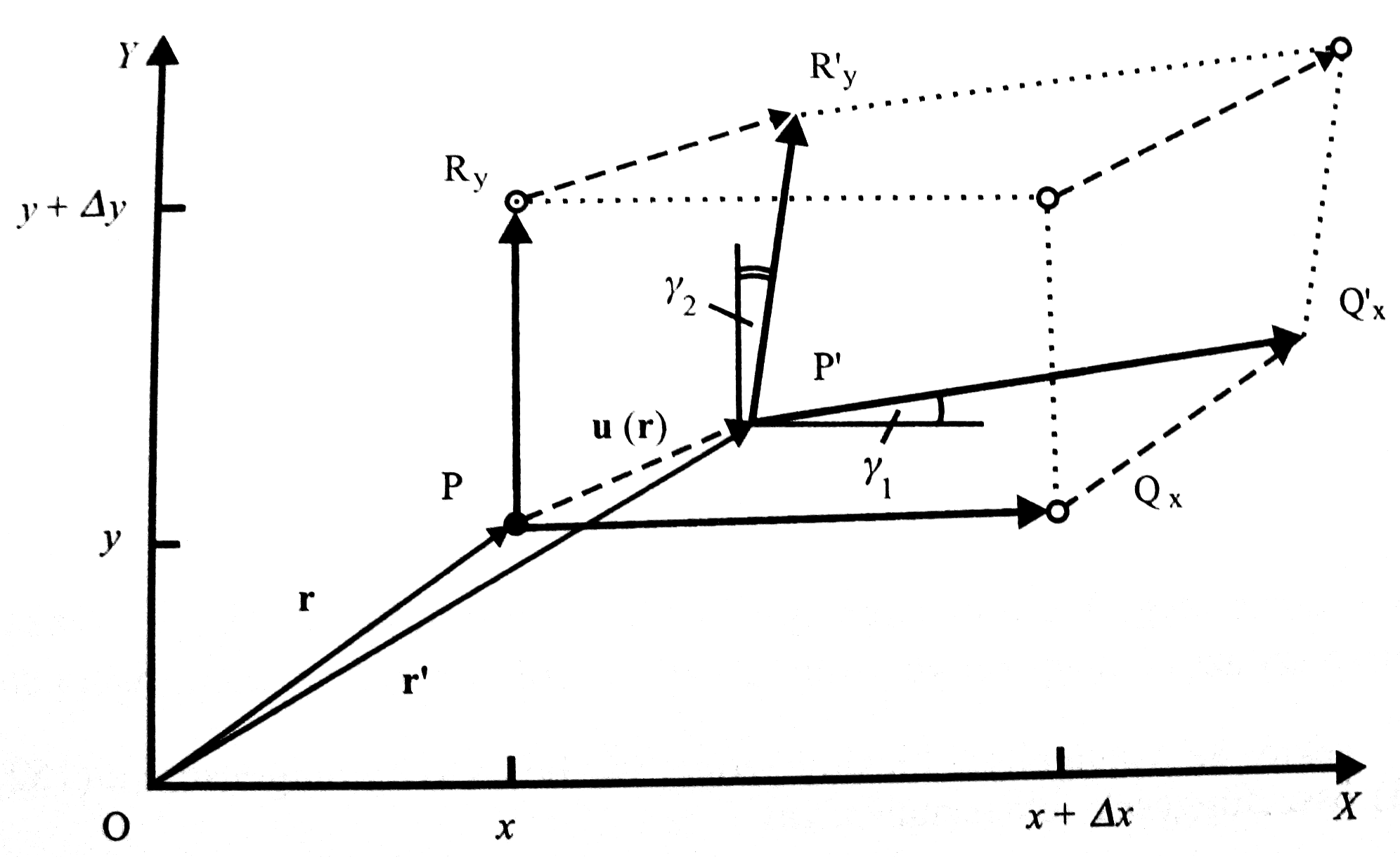
A P pont és környezete elmozdulása leírható egy egyszerű u(r) vektor-vektor függvénnyel.
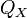 elmozdulásából
elmozdulásából 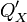 helykoordinátái:
helykoordinátái:
A  vektor x komponense:
vektor x komponense:
![\left(x+\Delta x\right)+u_{x}\left(x+\Delta x,y\right)-\left[x+u_{x}(x,y)\right]\simeq\Delta x\left(1+\frac{\partial u_{x}}{\partial x}\right)](/images/math/5/a/1/5a1f6da861d99d0795f538cccb01006c.png)
A  vektor y komponense:
vektor y komponense:
![y+u_{y}\left(x+\Delta x,y\right)-\left[y+u_{y}(x,y)\right]=\Delta x\left(\frac{\partial u_{y}}{\partial y}\right)](/images/math/5/9/1/591f79701cc24bdedd97f4c69d740736.png)
(Itt alkalmaztuk a skalár-vektor függvények megváltozására vonatkozó összefüggést:
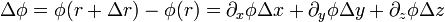 )
)
Az X-tengely irányában fekvő szakasz relatív megnyúlása tehát:
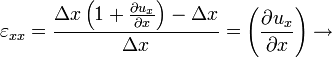 (A kettős index mutatja a szakasz irányát és a változás irányát is)
(A kettős index mutatja a szakasz irányát és a változás irányát is)
Ugyanezzel a gondolatmenettel: 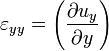
A  vektor Y tengellyel bezárt szöge:
vektor Y tengellyel bezárt szöge: 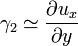 , ami alapján a nyírás szöge:
, ami alapján a nyírás szöge:
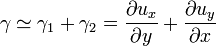 .
.
Tehát a az alakváltozást leíró elmoztulásfüggvény parciális deriváltjai közvetlen fizikai jelentéssel bírnak.
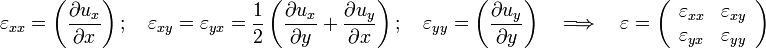 ,
,
ahol  a deformációs tenzor.
a deformációs tenzor.
Általánosan 3D-ban: 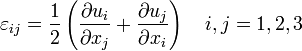
Ennek főátlóbeli komponensei a koordinátatengelyek irányában történő hosszváltozásokat, a vegyes indexű tagok a hozzájuk tartozó egyenesek közötti szögváltozások felével egyenlőek. A tenzor spurja a relatív térfogatváltozást adja meg. Fontos tétel még, hogy tetszőleges deformáció felírható egyenletes összenyomás és egy nyírás összegeként.
Általános Hooke-féle törvény
Éremes a Hooke-törvényt olyan deformációkra általánosítani, amelyek során a feszültség-tenzor elemei a deformációs-tenzor elemeinek lineáris függvényei. Mivel ezek a tenzorok szimmetrikusak, így hat független elemük van, és helyettesíthetők a következő kifejezéssekkel:
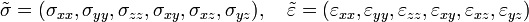
És az általános Hooke-törvény szerint ezek közt lineáris kapcsolat van:  , ahol
, ahol 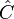 egy 6x6-os mátrix és a rugalmas állandók tenzora (ez is mindig szimmetrikus). Komponensekkel felírva:
egy 6x6-os mátrix és a rugalmas állandók tenzora (ez is mindig szimmetrikus). Komponensekkel felírva: 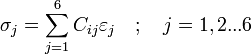
Tehát az általános Hooke-törvény egy 6 egyenletből álló egyenletrendszer, melyhez 36 rugalmas állandó szükséges. Ha figyelembe vesszük, hogy C is szimmetrikus, a deformáció homogén és izotrop és a koordináta rendszert is úgy választjuk, hogy a tengelyek egybeessenek a főfeszültségi irányokkal, akkor a Hooke-törvény 3 egyenletre egyszerűsödik:
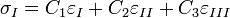
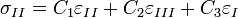
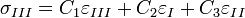
ahol 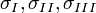 a főfeszültségek,
a főfeszültségek, 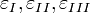 a fődilatációk,
a fődilatációk, 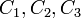 pedig a rugalmas állandók. Mivel a
pedig a rugalmas állandók. Mivel a 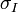 irányra merőleges másik két irány közül egyik sem kitüntetett, ezért
irányra merőleges másik két irány közül egyik sem kitüntetett, ezért 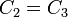 . Így bevezethetőek a következő jelölések:
. Így bevezethetőek a következő jelölések:
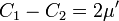 és
és 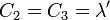
Ezekkel a fenti egyenletek átírhatók:
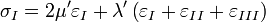

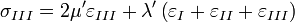
Tehát izotrop test esetén a deformáció és a feszültség állapot között két rugalmas állandó teremt kapcsolatot, melyek itt 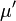 és
és 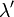 . Ezeket hívjuk Lamé-féle állandóknak. Ezek segítségével a korábban definiált deformációk állandói felírhatóak, néhány példa:
Young modulus:
. Ezeket hívjuk Lamé-féle állandóknak. Ezek segítségével a korábban definiált deformációk állandói felírhatóak, néhány példa:
Young modulus:
A Poisson-szám (itt most :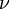 ):
):
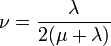 \
\
Kis deformációkra a kompresszibilitás:
Nyírási modulus:
A kompresszibilitás és a hangsebesség
Érdemes még tudni két differenciális összefüggést a deformálható anyagokkal kapcsolatban, az egyik a kompresszibilitás:
A másik a hangsebesség:
Hullámterjedés deformálható testekben, Doppler-effektus. [2]
Rugalmas hullám: rugalmas közegben keltett deformáció térbeli terjedése.
Attól függően, hogy gömb vagy sík mentén terjed a hullám, beszélhetünk gömb- vagy síkhullámról.
- Transzverzális hullám: a részecskék elmozdulása merőleges a terjedés irányára
- Longitudinális hullám: a részecskék elmozdulása megegyezik a terjedés irányával
Transzverzális hullámok terjedési sebessége:
Egy kötélen levő hullám-hegy terjedését vizsgáljuk. Felfoghatjuk úgy, hogy a hullám csúcsa (egy, a csúcs mozgásához rögzített koordinátarendszerben) hullámsebességű körmozgást végez. Ehhez a centripetális erőt a kötél két végén levő feszítőerők eredője adja.
Felhasználva, hogy 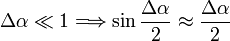
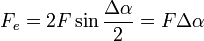
Az ív tömege: 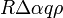 , ahol q a kötél keresztmetszete,
, ahol q a kötél keresztmetszete, 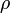 a sűrűsége.
a sűrűsége.
A körmozgás dinamikai egyenlete alapján:
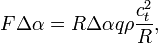 ahonnan a terjedési sebesség:
ahonnan a terjedési sebesség: 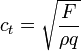
Bevezetve a kötélben levő húzófeszültséget: 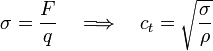
Hullámfüggvény
Egy kötél egyik felén T periódusidővel hullámokat keltünk. Egy periódusidő alatt a deformáció cT távolságra jut, ez a hullámhossz: 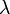 .
.
Egy általános pont rezgésére az összefüggés:
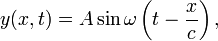 ahol
ahol
y a kötél kitérése, A a rezgés amplitúdója, 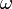 a körfrekvencia,
a körfrekvencia, 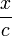 az adott ponthoz tartozó időkésés.
az adott ponthoz tartozó időkésés.
Ez a hullámfüggvény az eddigiek alapján átírható a következő alakba:
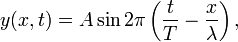 ahol ha bevezetjük a hullámszámot:
ahol ha bevezetjük a hullámszámot: 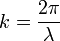
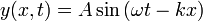 egyenletet kapjuk, mint végső formát.
egyenletet kapjuk, mint végső formát.
Hullám-tulajdonságok
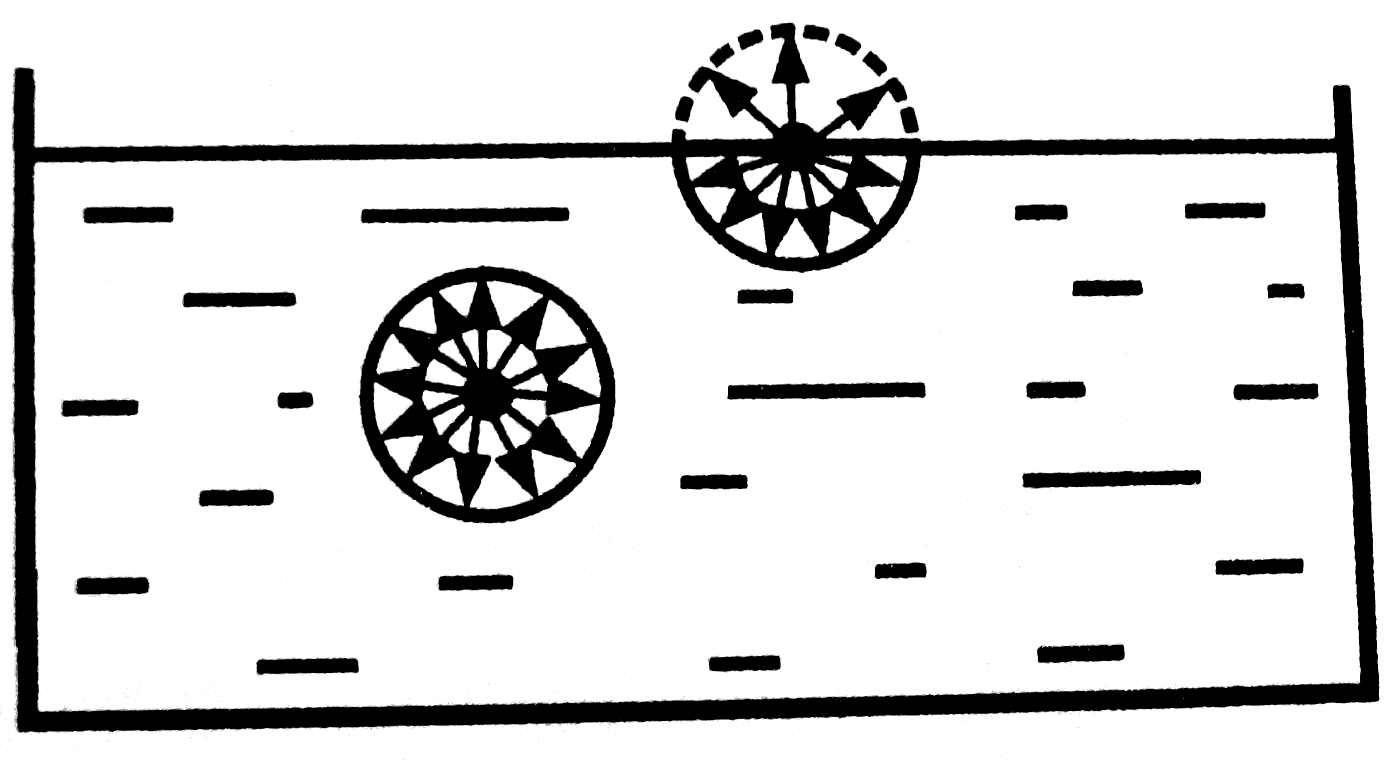
A tulajdonságok demonstrálására jól alkalmas pl. a hullámkád...
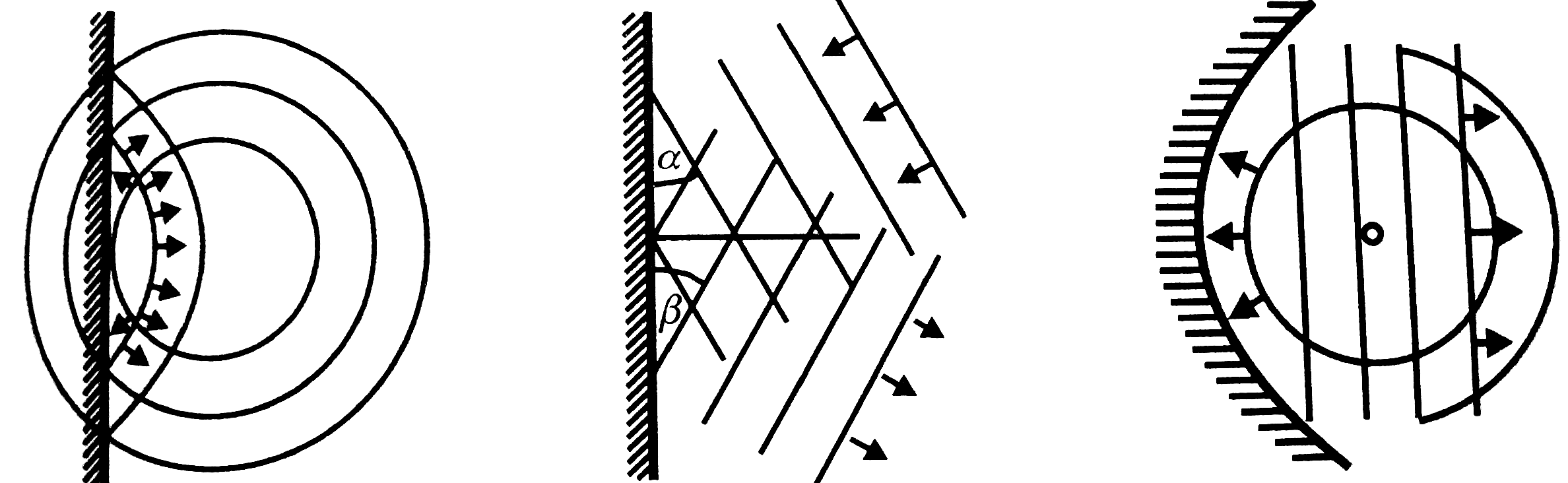
Visszaverődés (reflexió):
Az akadályhoz érkező és visszavert egyenes síkhullám ugyanakkora szöget zárnak be a fallal.
Törés (refrakció):
Pl. ha megváltozik a medence mélysége, akkor az más közegnek számít. A mélyebb vízben gerjesztett, adott hullámhosszúságú, egyenes hullámok a határfelületen irányváltozást és hullámhossz-rövidülést szenvednek.
Interferencia:
Két pont pontszerű hullámforrás a víz felszínén állandó interferenciakképet mutat.
A létrehozott körhullámok hol erősítik, hol kioltják egymást. A két hullámegyenlet:
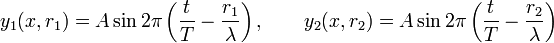
A két hullám fáziskülönbsége egy adott P pontban: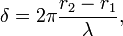 útkülönbsége:
útkülönbsége: 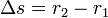
Erősítés maximális helye ott van, ahol 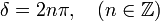 illetve
illetve 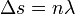
Kioltás pedig, ahol 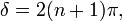 és
és 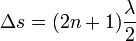
Elhajlás (diffrakció):
Ha hullámvonulat útjába akadályt teszünk, melyen rést hagyunk, akkor azt tapasztaljuk hogy a fal mögötti "árnyéktérben” is keletkeznek hullámok. Sőt, ha a rés a hullámhosszal egy nagyságrendű, illetve kisebb, akkor a rés mögött körhullámok keletkeznek (mint egy pontforrás esetén).
Ez magyarázható a Huygens-elvvel, mely szerint:
- A hullámfelületek minden pontjából elemi hullámok indulnak ki
- Az új hullámfelületet egy későbbi időpontban az elemi hullámok burkoló felülete adja.
Doppler-effektus
Ha egy hullámforrás mozog a közeghez viszonyítva, akkor a forrás előtt a hullámoknál hullámhossz rövidülés, mögötte hullámhossz növekedés figyelhető meg. Ennek megfelelően a mozgás irányában nagyobb a rezgés frekvenciája, mint a mögötte levő térrészben. Ez a Doppler- effektus.
Nézzük a hangtani esetet, mert ez “látványos”. Ha feltesszük, hogy a megfigyelő nem mozdul, a forrás közeledik, illetve hogy a terjedési sebesség kisebb, mint a hangsebesség (v < c), akkor a frekvenciaváltozás a következőképp adható meg:
A forrás egységnyi idő alatt f darab hullámot bocsájt ki, melyekből az első c távolságra jut. Ez alatt v távolságra jut a forrás, tehát az f darab hullámnak c-v hosszon kell elhelyezkednie, ami csak úgy lehet, ha megváltozik a hullámhosszuk:
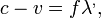 ahol
ahol 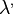 az észlelt hullámszám.
az észlelt hullámszám.
Az észlelt frekvencia pedig:
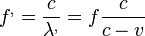
Ugyanezen gondolatmenet alapján, ha távolodik a forrás: 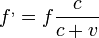
Hasonló gondolatmenet alapján, ha nyugvó forrásnál közeledik/távolodik az észlelő: 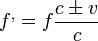
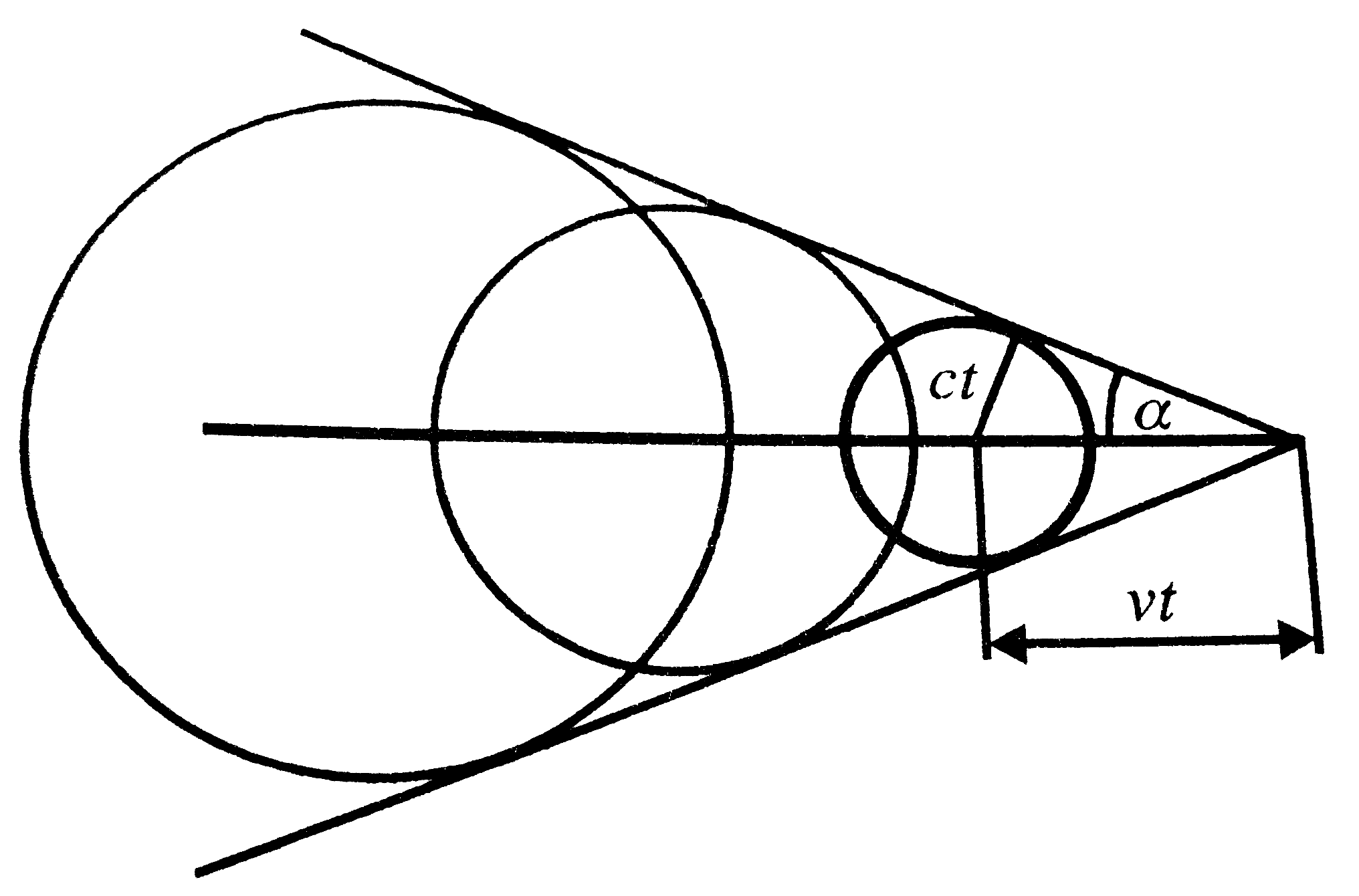
Ha a hullámforrás gyorsabban mozog a hangsebességnél, akkor a hanghullámok már nem tudják megelőzni a forrást:
A hang ekkor olyan kúpfelület mentén terjed, melynek csúcsában a hangforrás van. Az ábra alapján a kúp nyílásszöge:
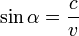 (Ennek reciprokát nevezzük Mach-számnak [M])
(Ennek reciprokát nevezzük Mach-számnak [M])
Folyadékok tulajdonságai
Hidrosztatika
Pascal-törvény: A nyomás a folyadékokban egyenletesen tejed, vagyis a külső nyomásból származó nyomás a folyadék belsejében és a határfelületén minden iránybban uagyanakkora.
Demonstrációs példák:
• Vizibuzogány: minden irányban egyenlő mértékben áramlik ki a víz.
• Vékonyfalú üvegpohárban (bolognai) üvegcsepp: ha megroppantjuk a csepp végét, akkor az üveg porrá esik szét és a gyors folyamat széttöri a poharat is.
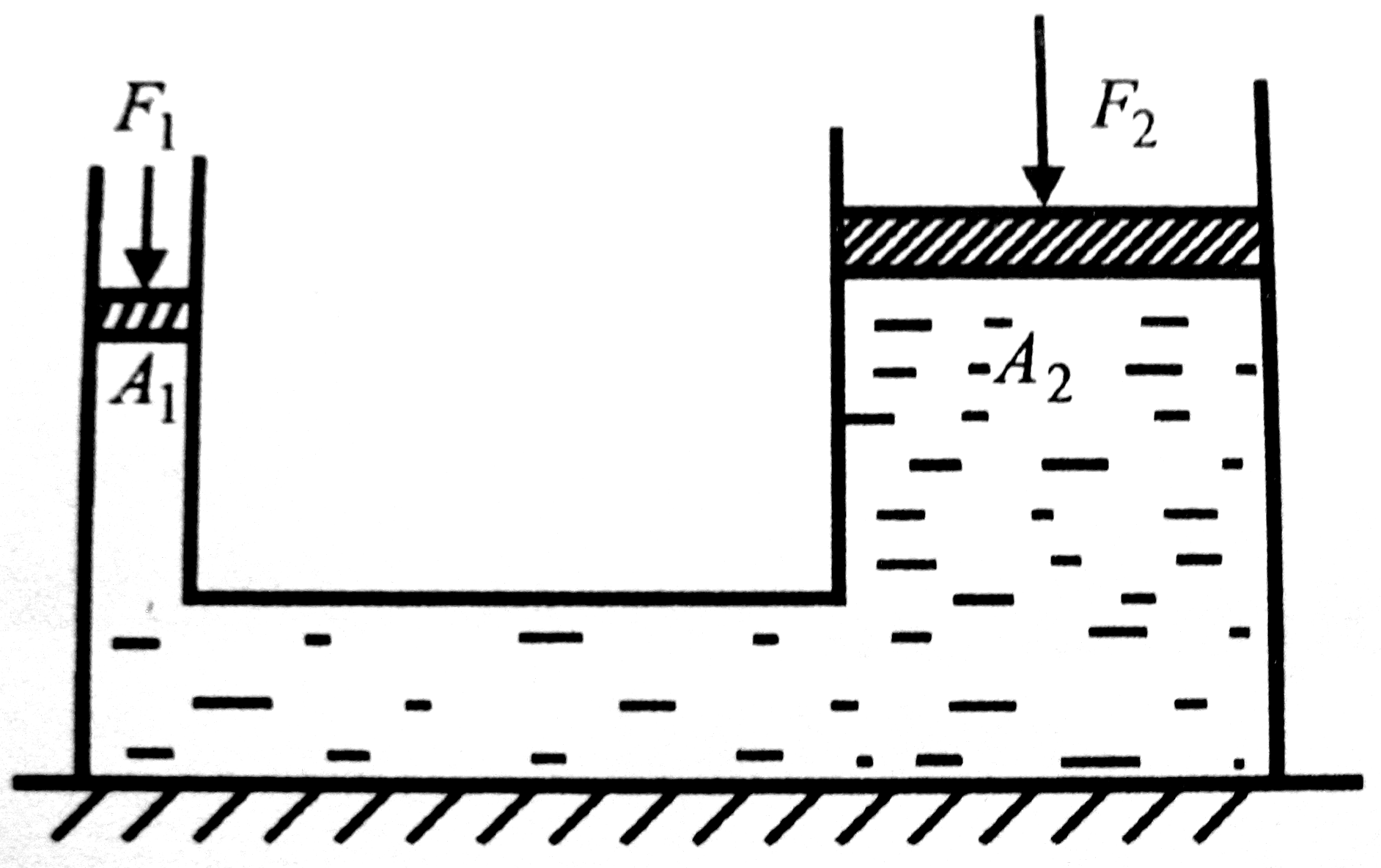
• Hidraulikus emelő: 
A hidrosztatikai nyomás egyenesen arányos a felszíntől mért mélységgel és a folyadék sűrűségével:
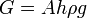 (A - a folyadék oszlop alapterülete, h - a magassága,
(A - a folyadék oszlop alapterülete, h - a magassága, 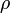 - a sűrűsége)
- a sűrűsége)
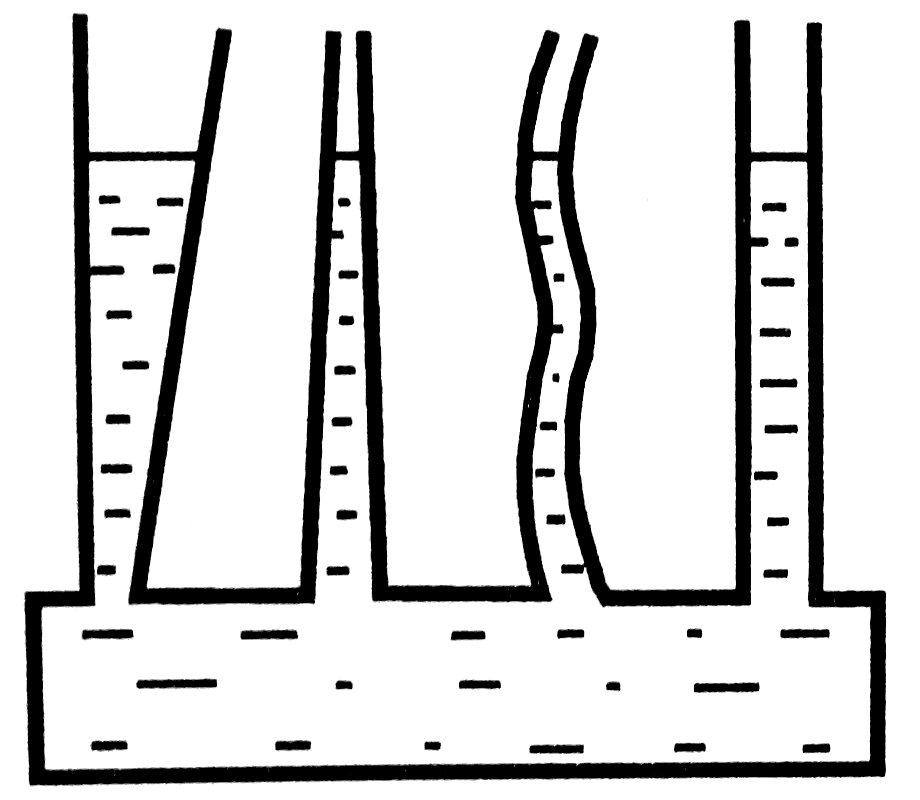
A hidrosztatikai paradoxon: Különböző formájú, de azonos alapterületű edények esetén a mérleg egyensúly mutat, ha ugyanakkora magasságú folyadék van bennük. (Ilyenkor is a folyadék oszlop nyomása fontos... “Az edény fala vagy tartja, vagy nyomja a folyadékot”)
Közlekedő edények: Szintén a Pascal-törvény értelmében (és a fentiek alapján is látható), a folyadékszint az ábrán látható rendszerben ugyanolyan magasan lesz mindenhol. (A hidrosztatikai nyomások egyenlőek!)
Felhajtóerő
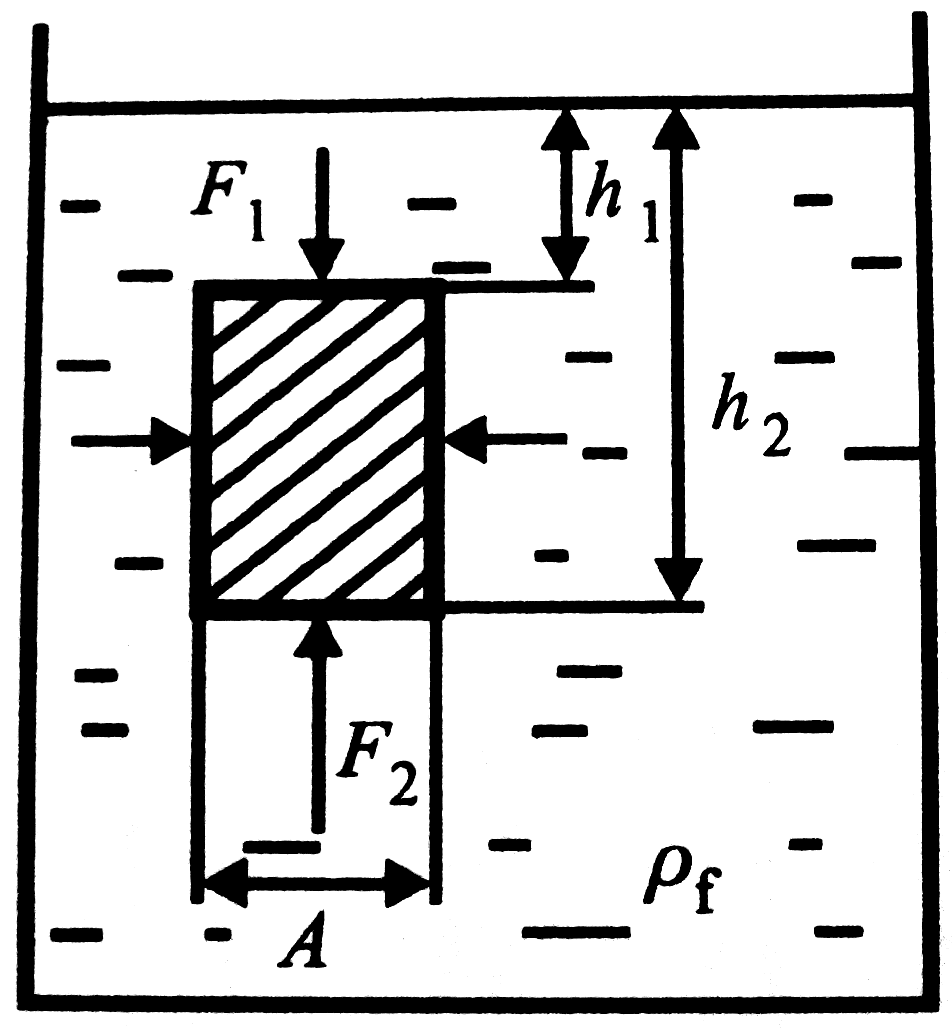
Egyszerű alakú testre (h magasságú, A keresztmetszetű henger sűrűségű folyadékba) a felhajtóerő:
A hidrosztatikai nyomásnál az oldallapra ható erők eredője 0, az alsó és felső lapra hatók összege pedig megadja a felhajtóerőt:
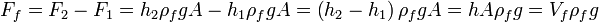
Ez a törvény általánosan is igaz: bármely folyadékba merülő testre a test által kiszorított folyadék súlyával megegyező nagyságú felhajtőerő hat. Ez Archimédész törvénye.
A testek úszása és annak stabilitása
Attól függően, hogy a test súlya vagy a testre ható felhajtó erő nagyobb, a test úszhat, elmerülhet vagy lebeghet.
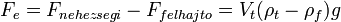
• Ha 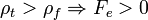 : a test elmerül
: a test elmerül
• Ha 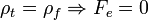 : a test lebeg
: a test lebeg
• Ha 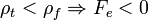 : a test úszni fog.
: a test úszni fog.
Úszás esetén a test részben belemerül a folyadékba úgy, hogy 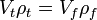 feltétel teljesüljön (ahol
feltétel teljesüljön (ahol 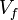 a test folyadékban levő része).
a test folyadékban levő része).
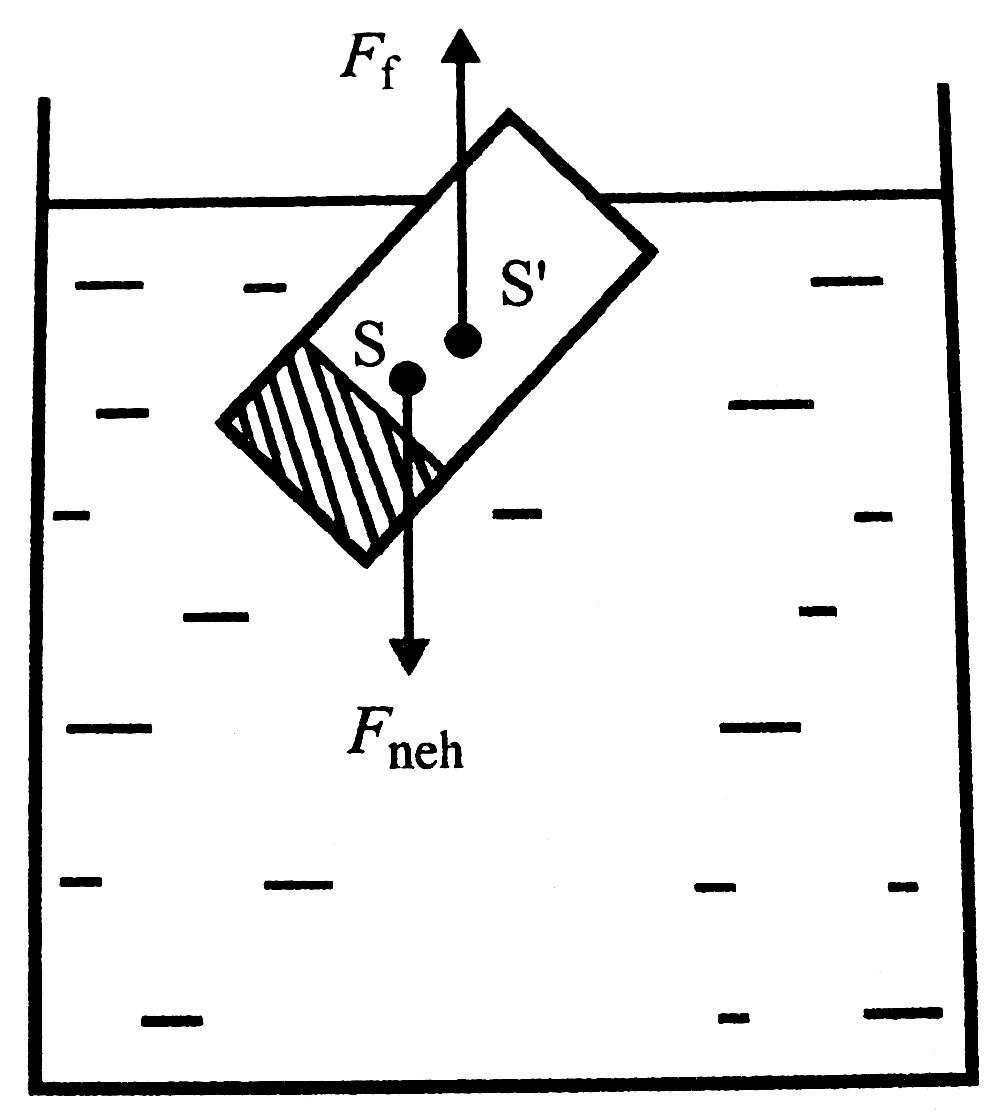
Ahhoz, hogy stabil úszásról beszéljünk, további feltétel szükséges: a felhajtó- és a nehézségi erő ne fejtsen ki forgatónyomatékot. Hiszen a test súlypontja (S) és a kiszorított folyadék súlypontja (S') nem mindig esik egybe.
Ha a kibillentett úszó test vissza áll eredeti helyzetébe, akkor stabilis az úszás. Ha ha kibillentve mindig ugyanúgy marad, akkor az egyensúlyi helyzet indifferens (pl. homogén gömb esetén). Ha pedig másik helyzetbe megy át, akkor labilis volt.
Felületi feszültség
Ha megnézzük egy folyadék molekula hatásgömbjét a folyadékon beljebb, akkor azt láthatjuk, hogy a kölcsönhatások eloszlása jóformán egyenletes. Viszont a felületen levő molekulákra ez nem igaz.
Tehát kísérletek és elméleti számítások alapján a felszíni réteg lazább, nagyobb az átlagos molekulatávolság, mint a folyadék belsejében. Ezért a felületi réteg feszítetté válik. És ennek a felszínnek a növeléséhez/átszakításához munkát kell végeznünk.
Ha egy keretre - aminek egyik oldala mozgatható - szappanhártyát feszítünk ki, akkor azt tapasztaljuk, hogy az erő (ami húzza az l hosszúságú oldalt) nem függ a hártya területétől:
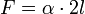
Ebből arra következtethetünk, hogy összehúzódáskor a hártya szerkezete/struktúrája nem változik. Továbbá a potenciális energiaminimum-elve következében létrejönnek a minimálfelületek. Az energiaminimumot pedig a felületi energia minimuma adja. (pl.: szappanos vízbe mártott kocka...)
Görbült felület görbületi nyomása:
Az adott hártyadarabka nyomását a következő összefüggéssel kaphatjuk meg, mely Laplace I. törvénye:

(Ennek segítségével lehet magyarázni a kapilláris emelkedést is [3])
Nedvesítő és nem nedvesítő folyadékok:
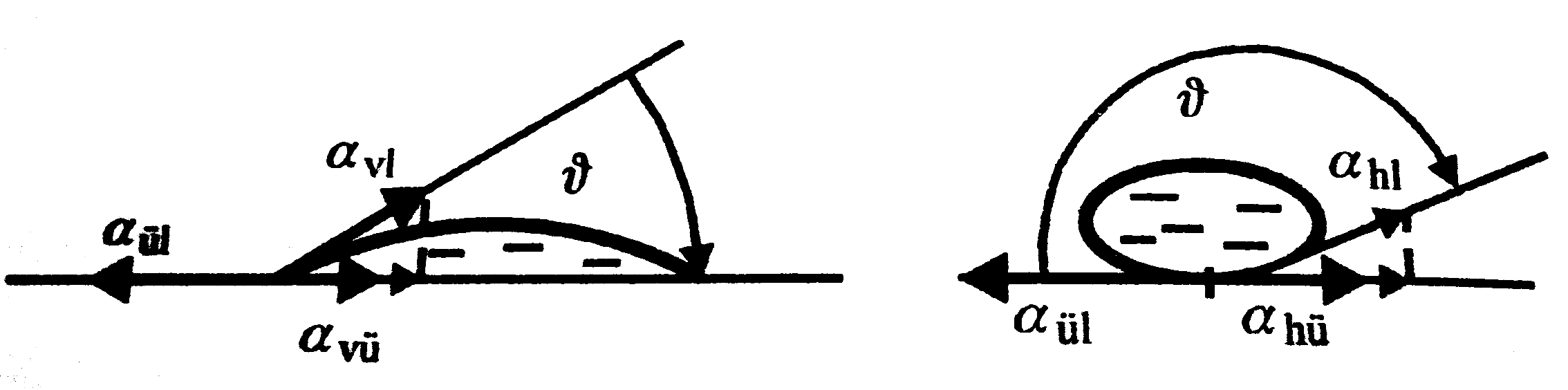
Az üvegre cseppentett folyadékok alakját a nehézségi erő és a felületi feszültség együttesen alakítják ki.
Az ábrán láthatóak a 3 anyag érintkezési vonalában ható felületi feszültségek. (Jelmayarázat: v-víz, h-higany, ü-üveg, l-levegő) Az egyensúlyt a következő összefüggés írja le:
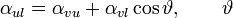 az illeszkedési szög. (Higanyra hasonló az egyenlet.)
az illeszkedési szög. (Higanyra hasonló az egyenlet.)
Ezt az összefüggést nevezzük Laplace II. törvényének.
Torricelli-kísérlet
A levegő súlyából adódó légnyomás meghatározásához Torrichelli egy 1 m hosszú kémcsövet megtöltött higannyal és higgannyal telt edénybe helyezte a cső nyitott végét. A csőben a higany szintje az edényben levő higanyhoz képest 76 cm-re esett (függetlenül az üvegcső dőlésszögétől). Ezzel a magasságú higannyal tud a levegő nyomása egyensúlyt tartani (közlekedő edények elve).
További példák: befőttes üveg behorpadt celofánnal, magdeburgi féltekék....
Áramlások
Lagrange-féle leírás
Folyadékot a szilárd testekhez hasonlóan kezeljük, és részekre bontjuk. Majd minden részelemnek külön megadjuk a helykoordinátáját és a pályavonalát. De ez a felírás nagyobb időre túl kusza pályákat eredményez.
Euler-féle leírás
Nem a közeg egyes pontjait, hanem az áramlási teret nézzük a következőképp: minden pontban megadjuk a sebességet (v), a nyomást (p) és a sűrűséget (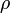 ) időtől függően. Ekkor nem számít, hogy egy adott részecske éppen hol tartózkodik. A szemléltetéshez használjuk az áramvonalakat, melynek deriváltja megadja az adott pontban a sebességvektor egyenesét.
) időtől függően. Ekkor nem számít, hogy egy adott részecske éppen hol tartózkodik. A szemléltetéshez használjuk az áramvonalakat, melynek deriváltja megadja az adott pontban a sebességvektor egyenesét.
Áramlási cső: az áramlási térben egy elméleti zárt görbe pontjain ármenő áramvonalak összessége.
Áramlások osztályozása:
• Súrlódásos/súrlódás mentes: súrlódásos, ha a folyadékrészek relatív mozgásából származó nyíróerők nem elhanyagolhatók.
• Örvényes/örvény mentes: örvényes, ha a folyadékrészek forgómozgást is végeznek.
• Stacionárius/nem stacionárius: stacionárius, ha v,p és 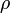 nem függnek az időtől.
nem függnek az időtől.
Tökéletes folyadék áramlása
Vegyünk egy 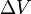 térfogatú folyadék részecskét egy r(x,y,z) helyen. A rá ható erők x komponense az X-tengelyre merőleges lapjaira ható nyomásból származik. Így:
térfogatú folyadék részecskét egy r(x,y,z) helyen. A rá ható erők x komponense az X-tengelyre merőleges lapjaira ható nyomásból származik. Így:
![F_{x}=\left[p(x,y,z,t)-p(x+\Delta x,y,z,t)\right]\Delta y\Delta z=-\frac{\partial p}{\partial x}\Delta x\Delta y\Delta z](/images/math/c/4/3/c43c289024c9e0a823e7f328838cb845.png)
Felhasználva, hogy 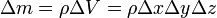 , a részecske mozgásegyenletének x komponense:
, a részecske mozgásegyenletének x komponense:
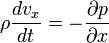 ugyanez felírható az y komponensre is.
ugyanez felírható az y komponensre is.
A z komponensnél viszont figyelembe kell venni a nehézségi erőt: 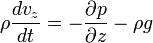
Vektoriálisan megkapjuk az ideális folyadékokra vonatkozó dinamikai alapegyenletet(Euler-egyenlet):
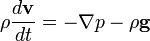
Ahol a teljes időderivált kifejtésénél figyelembe kell venni azt, hogy mire kis idő múlva odanézek, a részecske már nem ott lesz, ahol eddig volt, így a deriváltat a láncszabály szerint írhatjuk le:
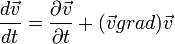
Ez az egyenlet még nem elég az áramlás problémájának megoldásához, hiszen ez csak 3 egyenlet míg az ismeretlenjeink száma: 3(sebességek)+1(nyomás)+1(sűrűség) Kell még a kontinuitási egyenlet és egy állapotegyenlet.
A peremfeltételek nem súrlódó folyadék esetén azt mondják, hogy a sebesség a falakra merőleges komponense 0.
Kontinuitási egyenlet:
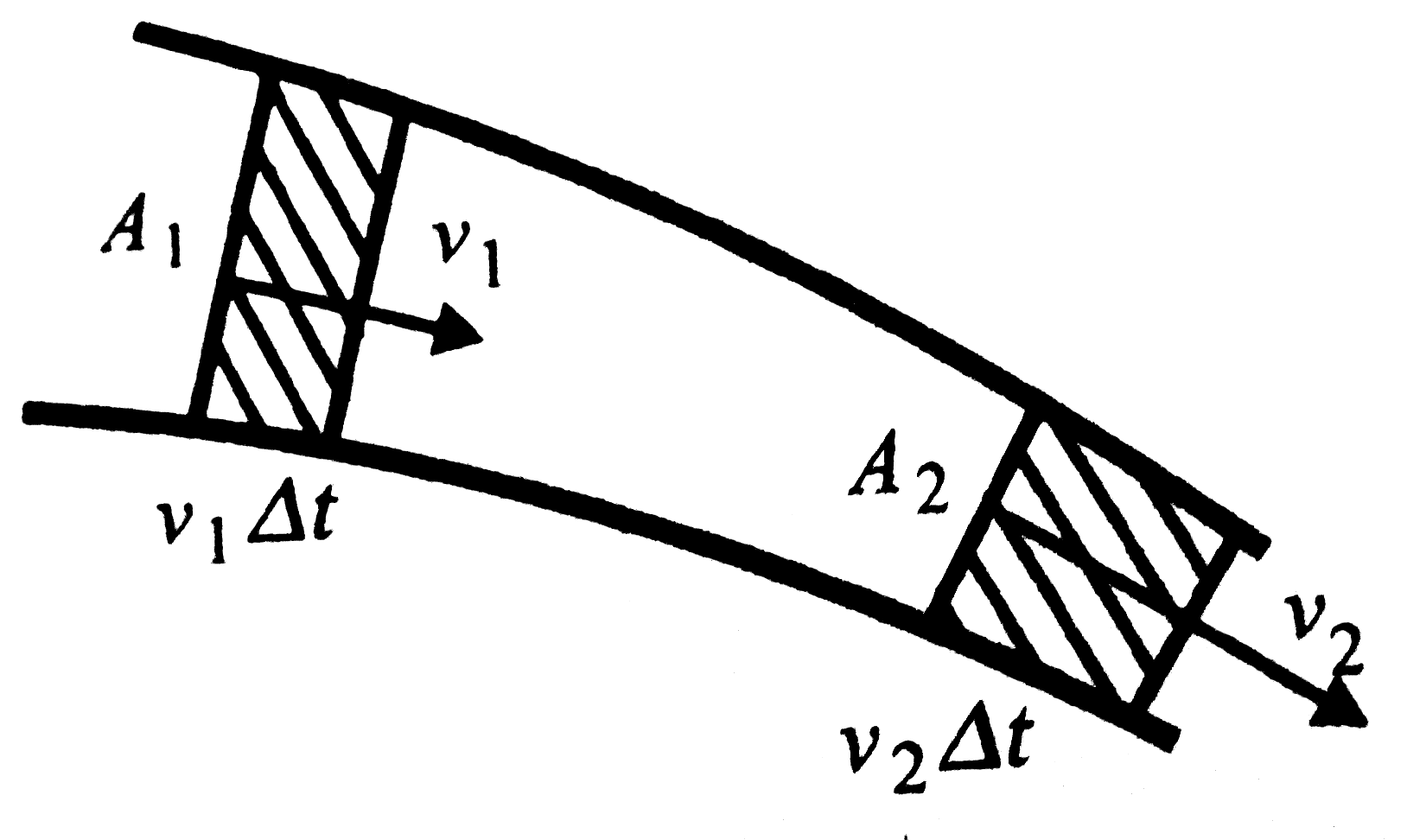
Az összenyomhatatlanság miatt az áramlási cső két tetszőleges keresztmetszetén egyenlő térfogatú folyadég halad keresztül.
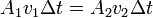 , ahonnan:
, ahonnan: 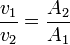 adódik, ami a stacionárius áramlásra vonatkozó kontinuitási egyenlet. Szűkületben tehát nagyobb sebességgel áramlik a folyadék.
adódik, ami a stacionárius áramlásra vonatkozó kontinuitási egyenlet. Szűkületben tehát nagyobb sebességgel áramlik a folyadék.
Általános esetben a kontinuitási egyenlet a következőképpen írható fel:
- Egy térfogatot kiválasztva a folyadékon belül, a térfogaton belüli tömeg megváltozása:
- Ennek egyenlőnek kell lennie a térfogat szélein(felületén) kiáramlott tömeggel:
A felületi integrálra Gauss-Oszrogradszkij tételt alkalmazva, majd kihasználva, hogy ez minden térfogatra igaz, kapjuk a szokásos alakú kontinuitási egyenletet:
A leggykrabban választott állapotegyenlet 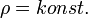 vagyis az összenyomhatatlan folyadék esete. Ekkor az előző egyenlet így egyszerűsödik:
vagyis az összenyomhatatlan folyadék esete. Ekkor az előző egyenlet így egyszerűsödik:
A Bernoulli-egyenlet
Vizsgáljuk meg az ABCD folyadék rész elmozdulását (A'B'C'D'-be megy át 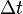 idő múlva). Mivel az ábrán fehéren hagyott rész nem változik az áramlás szempontjából, ezért úgy tekintjük, mintha ABA'B' folyadék CDC'D'-be jutott volna át. A munkatétel szerint a folyadék mozgásenergiája megegyezik a ráható erők munkájának összegével. Súrlódásmentes esetben csak a nehézségi erő és a
idő múlva). Mivel az ábrán fehéren hagyott rész nem változik az áramlás szempontjából, ezért úgy tekintjük, mintha ABA'B' folyadék CDC'D'-be jutott volna át. A munkatétel szerint a folyadék mozgásenergiája megegyezik a ráható erők munkájának összegével. Súrlódásmentes esetben csak a nehézségi erő és a  nyomásokból származó erőt kell figyelembe venni. A nehézségi erő munkája:
nyomásokból származó erőt kell figyelembe venni. A nehézségi erő munkája:

A nyomóerőé pedig:
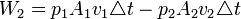
Felhasználva a kontinuitási egyenletet: 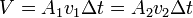 , és a munkatételt:
, és a munkatételt:
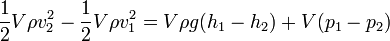 , melyet átrendezve a következő összefüggést kapjuk:
, melyet átrendezve a következő összefüggést kapjuk:
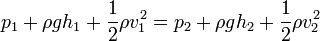
Ezt az összefüggést hívjuk Bernoulli-egyenletnek. Ez alapján ez az összeg bármely áramfonal esetén állandó - összenyomhatatlan folyadék súrlódásmentes, stacionárius áramlása esetén:
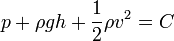
Viszkózus folyadék áramlása
Amikor a folyadékrészek relatív sebességük nem 0, akkor a részek közötti belső súrlódási erő már nem hanyagolható el általában.
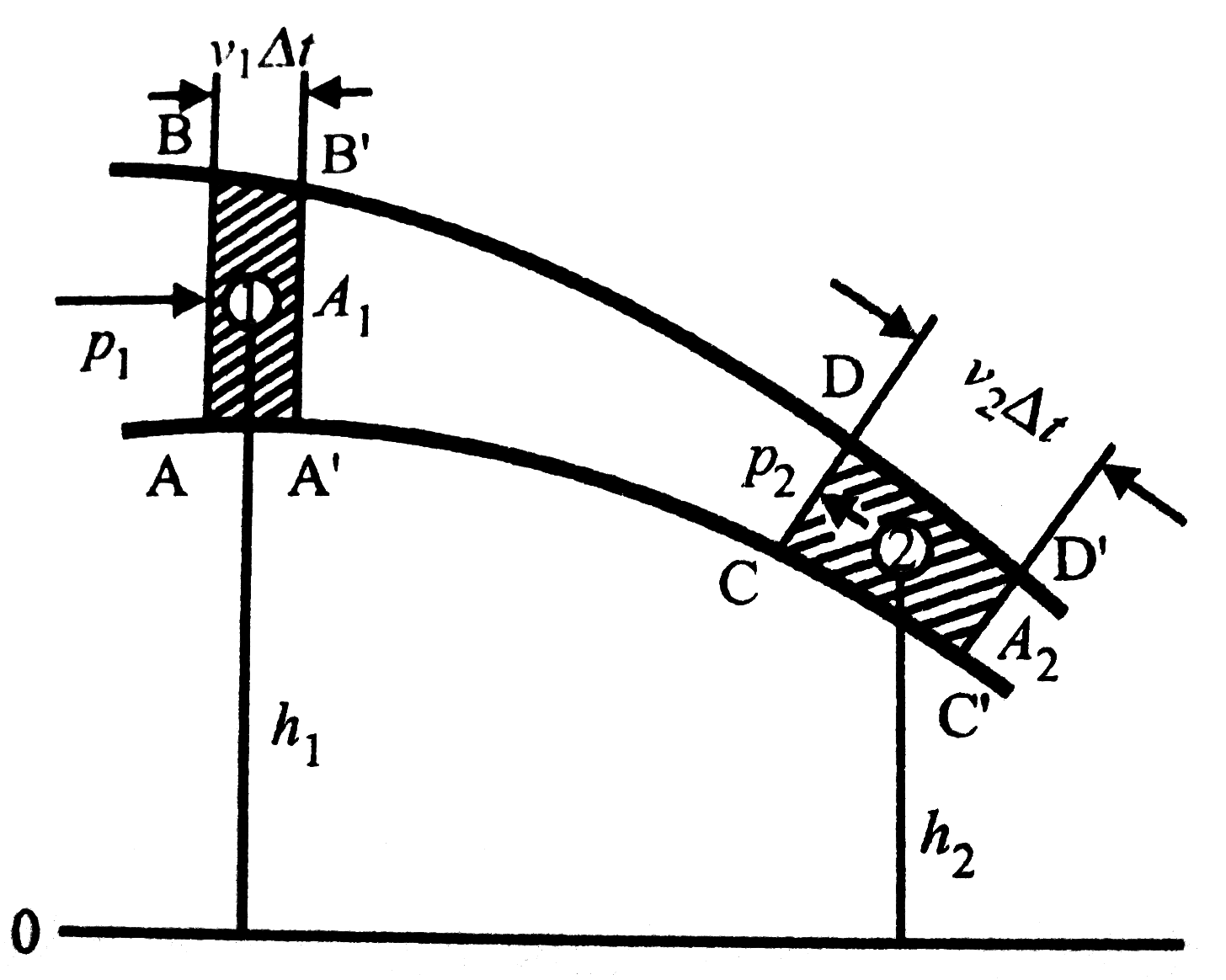
Tapasztalat: egymásra rétegzett színes és színtelen glicerinből kihúzunk egy üveglapot. Az üveglapon lévő folyadékok sebessége a legnagyobb, a távolabbiaké kisebb. A relatív sebesség és belső súrlódás miatt a lasabb rétegek lassítják a gyorsabbakat és fordítva.
Mégjobban vizsgálható, ha két párhuzamos lap közötti folyadék áramlását vizsgáljuk, úgy hogy csak a felső lapot mozdítjuk el.
Ekkor legfelül a leggyorsabb a folyadék, míg legalul 0 a sebessége. Ekkor a folyadék sebességének az áramlásra merőlegesen gradiense van. Eredményül azt kapjuk, hogy a belső súrlódási erő egyenesen arányos az egymáson csúszó folyadékrétegek felületének nagyságával és a keresztmetszetben vett egységnyi távolságra eső sebességváltozással:
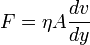
Ezt az összefüggést Newton belső súrlódási törvényének nevezzük. (Ahol 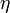 a dinamikai viszkozitás.)
a dinamikai viszkozitás.)
Stokes törvénye:
Áramlási térbe helyezett közelében réteges áramlás alakulhat ki. A belső súrlódással a közeg erőt fejt ki a golyóra, ami arányos a golyó relatív sebességével, a golyó sugarával, és a közeg dinamikai viszkozitásával:
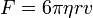
Ezt a törvényt használta fel Millikan is a kísérlete során, amikoris megmérte az elemi elektromos töltést.....
További pl.: Brown-mozgáskor felhasznált mozgásegyenlet: 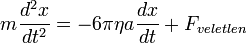
Turbulencia
Azt tapasztaljuk, hogy ha egy áramlási csőben lamináris (stacionárius) áramlás sebességét növeljük, akkor egy adott sebességnél az áramlás kavargó, turbulens áramlásba csap át. Ugyanezt tapasztaljuk, ha a sebességet nem vátoztatjuk, de az áramlási cső méretét növeljük. Egyes vizsgálatok alapján a turbulenssé válás függ az áramlási sebességtől (v), az áramlási cső harántméretétől (r), a közeg sűrűségétől (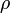 ) és a dinamikai viszkozitástól (
) és a dinamikai viszkozitástól (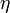 ). Az átmenet akkor történik meg, ha
). Az átmenet akkor történik meg, ha
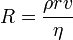 , ahol R a Reynolds-szám.
, ahol R a Reynolds-szám.
Ez a számérték hozzárendelhető az adott testekhez is, melyeket az áramlási csatornába helyezünk. Két test körüli áramlások pedig akkor lesznek hasonlóak, ha 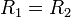 . (Tehát pl egy 10x kisebb repülőgép modellhez 10x nagyobb szél kell...)
. (Tehát pl egy 10x kisebb repülőgép modellhez 10x nagyobb szél kell...)
Áramlások hasonlósága
Az előző pontban említett Reynolds-szám csak egy a hidrodinamika rengeteg dimenziótlan száma közül. Általánosan elmondható, hogy két áramlás akkor hasonló, ha az adott probléma szempontjából jelentős dimenziótlan számai egyenlőek. Két áramlás hasonlósága alatt itt azt értjük, ha dimenziótlanított formában megegyező függvények írják le a sebesség és nyomáseloszlásukat(ha más lényeges változóink is vannak, pl.: hőmérséklet, akkor azokat is). Ennek óriási jelentősége van, mivel a hidrodinamika egyenletei nemlineárisak, és sokszor megfelelő közelítő megoldás sem található rájuk, így a mérnökök/kutatók kénytelenek modellkísérleteket alkalmazni, pl. a vizsgálandó hajótest kicsinyített másán.
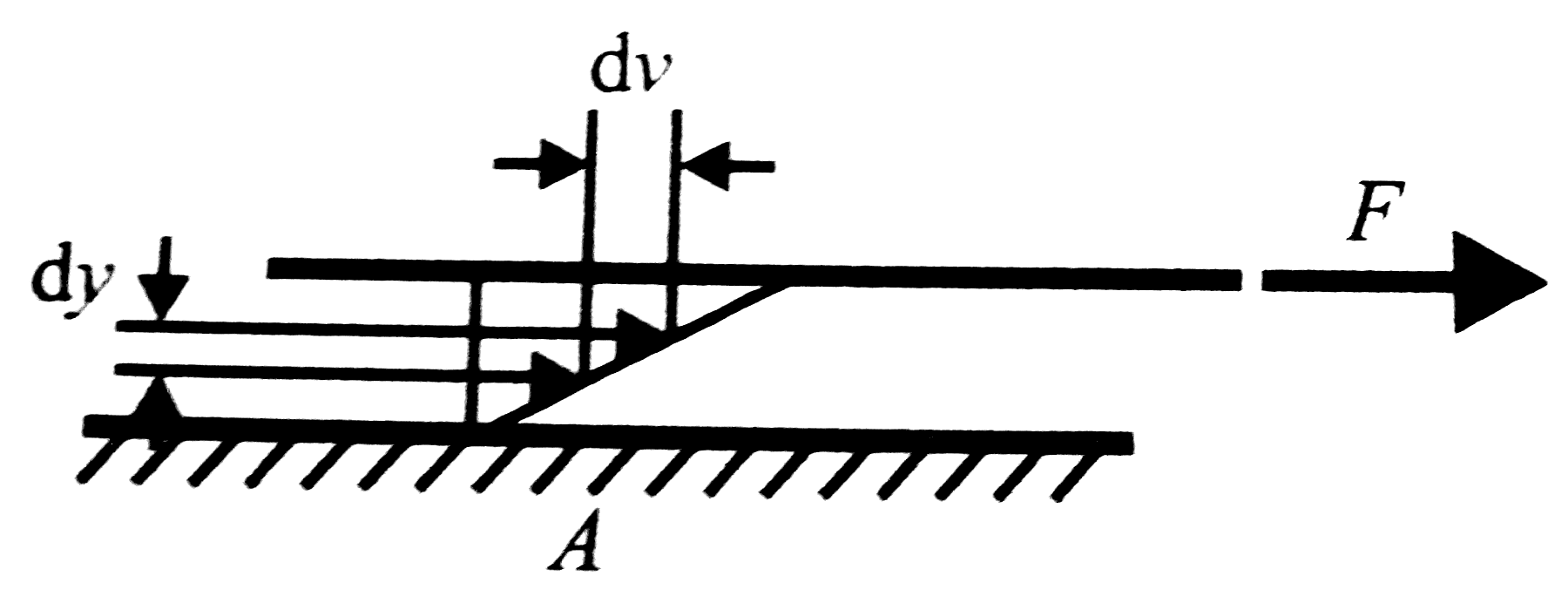
Örvények
Két, nem azonos sebességű lamináris áramlás határfelületén a nyíróerők vékony sávban forgásba hozzák a folyadékot, örvények jönnek létre.
Ha egy testet (pl. hengert) helyezünk lamináris áramlásba, akkor a testtől távolabb az áramlás nem változik, de a test közelében a folyadéknak nagy lesz az áramlásra merőleges sebesség-gradiense. (Ez a Prandtl-féle határréteg.) Ez amiatt van, mert a test felületén a folyadékrészek sebessége nulla, a határréteg másik szélén pedig maximális. A belső súrlódás miatt nem tudnak elhaladni a test mellett, hogy mögé jussanak (a magas nyomású részhez), hanem már hamarabb lefékeződnek és visszakanyarodnak a kisebb nyomású rész felé. Viszont itt a nagysebességű áramlás elkapja a visszaáramló folyadékot és így forgásba jön. Ez a kialakuló örvény egyre nagyobb lesz, majd leválik a testről. Ez a jelenség periódikusan ismétlődik, és ellentétesen forgó örvénypárok szakadnak le egymás után. Ezt nevezzük Kármán-féle örvénysornak.
Összenyomhatatlan folyadák esetén:
Az Euler-egyenlethez képesti egyetlen új tag a viszkozitás hatását írja le. 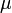 a kinenatikai viszkozitás
a kinenatikai viszkozitás
[4] A peremfeltételek viszkózus folyadékra azt mondják, hogy a falak mentén a víz áramlási sebessége nulla.
Hivatkozások: Forrás: Tasnádi-Skrapits-Bérces - Általános fizika I.2.
- ↑ könyv: 151§ 1. (50-51. oldal)
- ↑ Tasnádi-Skapits-Bérces: Általános fizika I.2. IV. C) Hullámtan
- ↑ 171.§ 1. (110. o)
- ↑ http://en.wikipedia.org/wiki/Navier-Stokes