Fenomenologikus termodinamika
Tartalomjegyzék
- 1 Az egyensúly állapota, nulladik főtétel, hőmérséklet
- 2 Első főtétel
- 3 Entalpia, reakcióhő
- 4 Különböző anyagok hőkapacitása
- 5 Állapotegyenletek
- 6 Speciális folyamatok ideális gázzal
- 7 Reális gázok
- 8 Carnot-körfolyamat
- 9 Az entrópia fogalma, második főtétel
- 10 A fundamentális egyenlet
- 11 Legendre-transzformáció, termodinamikai potenciálok
- 12 Szabadenergia
- 13 Maxwell-relációk
- 14 Szabadentalpia, kémiai affinitás
- 15 Az Euler-féle összefüggés, Gibbs-Duhem reláció
- 16 Hőerőgépek
- 17 Harmadik főtétel
- 18 Alacsony hőmérsékletek előállítása
- 19 Fázisátalakulások termodinamikai tárgyalása
- 20 Fázisegyensúlyok
Az egyensúly állapota, nulladik főtétel, hőmérséklet
Nulladik főtétel
A tapasztalat azt mutatja, hogy minden egyes termodinamikai kölcsönhatáshoz tartozik egy jellemző tulajdonság, amelynek a két testre vonatkozó egyenlősége az egyensúly szükséges és elegendő feltétele. Az ilyen tulajdonságokat empirikus intenzitásparamétereknek nevezzük. Ez a termodinamika nulladik főtétele.
| Közelhatás | Intenzitásparaméter |
|---|---|
| Mechanikai | Nyomás |
| Anyagi | Kémiai potenciál |
| Elektrosztatikus | Elektrosztatikus potenciál |
| Hőhatás | Hőmérséklet |
Empirikus hőmérsékleti skálák
Egy ilyen intenzitásparaméter a hőmérséklet is. Ha két test termikus kapcsolatban van, akkor energia áramolhat közöttük. Az empirikus hőmérséklet fogalom tehát:
- Termikus kapcsolatban lévő A és B testek energiát adhatnak át egymásnak. Ha az A ugyanannyi energiát ad át B-nek, mint B az A-nak, akkor azt mondjuk, hogy egyensúlyban vannak és hőmérsékletük egyenlő.
- Ha nincsenek egyensúlyban, akkor annak a testnek nagyobb a hőmérséklete, amely több energiát ad át a másiknak, mint amit a másik egyidejűleg visszaad neki. A nagyobb hőmérsékletű test ekkor tehát energiát veszít.
Ezzel még csak a kisebb-nagyobb kapcsolatot és az egyenlőséget állapítottuk meg, a tulajdonképpeni metrikánk hiányzik. Ezt önkényes választással lehet megválasztani. A legelterjedtebb empirikus skálák:
Celsius-skála: 101,325kPa légköri nyomáson a víz forráspontja 100°C, a jég olvadáspontja pedig 0°C, a beosztás a két hőmérséklet különbségének századrésze.
Kelvin-skála: Más néven ideálisgáz-skála. Az ideális gáz nyomása és hőmérséklete között T=Cp lineáris kapcsolatot feltételezve a nullapont természetesen adódik 0K=-273,15°C-nak, szükség van még egy pontra a skála meghatározásához, ez az az igen jól reprodukálható hőmérséklet lett, amikor 610,5Pa hármasponti nyomáson a víz, a vízgőz és a jég egyensúlban van, 0,01°C hőmérsékleten. A Kelvin fok egyenlő a víz hármaspontjához tartozó hőmérséklet 273,16-od részével. Így a Celsius és a Kelvin skála beosztása azonos. Az átváltás: 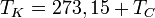
Hőmennyiség
A tapasztalat szerint a makroszkopikus testek melegítéskor/hűtésekor bekövetkező energiaváltozás egyenesen arányos a hőmérsékletváltozással:

Ahol a C hőkapacitás. Az itt szereplő 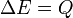 munkavégzés nélküli belső energia változást pedig hőmennyiségnek nevezzük. Magát a folyamatot, vagyis a munkavégzés és és mozgásmennyiség átadás nélküli energiaátadást pedig hőközlésnek.
munkavégzés nélküli belső energia változást pedig hőmennyiségnek nevezzük. Magát a folyamatot, vagyis a munkavégzés és és mozgásmennyiség átadás nélküli energiaátadást pedig hőközlésnek.
Első főtétel
Az első főtétel az energiamegmaradást fejezi ki. Egy termodinamikai rendszer belsőenergiáját kétféleképpen lehet megváltoztatni, hőközléssel és munkavégzéssel. Differenciális változás esetén:
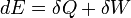
Itt 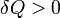 ha a rendszer hőt vesz fel,
ha a rendszer hőt vesz fel,  ha a környezet munkát végez a rendszeren.
ha a környezet munkát végez a rendszeren.
A főtétel kifejezésében a belső energia független állapothatározók függvénye, megváltozásának értéke csak a kezdeti és a végponttól függ, azt mondjuk, hogy a belső energia állapotfüggvény, vagy teljes differenciál. Ezzel szemben a munka és a hőátadás útfüggvények, értékük függ a folyamat pontos lezajlásától. A munka lehet térfogati munka -p dV, de lehet egyéb munka is, mint például az elektromos áram munkája. Állandó térfogaton a belsőenergia változása egyéb munkavégzés nélkül egyenlő a hőátadással:
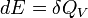
Entalpia, reakcióhő
Az entalpia definíció szerint:
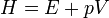
Az entalpia megváltozása:
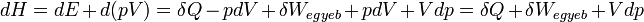
Vagyis ha nincs egyéb munka, akkor állandó nyomáson az entalpia megváltozása egyenlő a hőátadással:
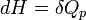
Ez az entalpiát különösen alkalmassá teszi kémiai reakciók tanulmányozására, hiszen ezek általában állandó nyomáson (légköri nyomáson) mennek végbe.
Az elektrokémia főtétele kimondja, hogy az entalpiaváltozás csak a reakcióban lévő anyagok kezdő és végállapotától függ, a reakció lefolyásától nem. Ez nyilvánvalóan következménye az első főtételnek, de történetileg előbb mondták ki. Ez azt jelenti, hogy ha ugyanahhoz a végállapothoz a kezdeti állapotból több különböző reakcióláncon keresztül is el lehet jutni, akkor az entalpiaváltozás szempontjából mindegy, hogy melyik ment végbe.
Különböző anyagok hőkapacitása
Általában kétféle hőkapacitásról szokás beszélni, az állandó nyomáson és az állandó térfogaton mérhetőről. A különböző anyagok hőkapacitásának becslése legegyszerűbben az ekvipartíció tétele segítségével tehető meg. Ez viszont már nem a fenomenologikus termodinamika tárgya, hanem a kinetikus elméleté és a statisztikus fizikáé. Ezért ezt itt nem vezetjük be külön, csak alkalmazzuk.
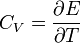 és
és 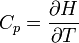
Egyatomos gázok
Az ekvipartíció tételből:
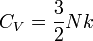 és
és 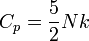
A kettő különbsége (Robert-Mayer egyenlet):
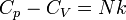
Kétatomos gázok
A kétatomos gázok esetében valamivel bonyolultabb a helyzet. Alacsony hőmérsékleten (100K alatt) a moláris hőkapacitásuk 3R/2, vagyis mintha csak transzlációs mozgást végeznének, szobahőmérséklet környékén a moláris hőkapacitásuk 5R/2, mert ekkor már a forgási szabadsági fokaik is megjelennek, magas hőmérsékleten (1000K felett) pedig 7R/2, ekkor már ugyanis a rezgési szabadsági fokok is megjelennek. Ez a tapasztalat a klasszikus ekvipartíció tételnek ellent mond, értelmezése a kvantummechanika segítségével lehetséges. Lásd a Kvantumstatisztikák-nál.
Többatomos gázok
Szobahőmérsékleten moláris hőkapacitásuk közelíthető 3R-ként. Általában a helyzet bonyolultabb, akárcsak az előző esetben.
Szilárd anyagok
Szilárd anyagokat független 3D-s oszcillátorokként elképzelve a moláris hőkapacitásra 3R adódik. Ez már az ekvipartíció előtt ismert tapasztalati törvény, a Dulong-Petit szabály. Azonban ez sem lesz mindig igaz, alacsony hőmérsékleten a kvantumos effektusok miatt a hőkapacitás csökken, 0K hőmérséklethez tartva 0-hoz tart.
Állapotegyenletek
Valamilyen összefüggés a makroszkopikus paraméterek között.
Ideális gáz
A gáz ideális, ha pontszerűek a részecskéi, és nem hatnak kölcsön egymással. Ebből kifolyólag a gáz annál ideálisabb, minél melegebb és ritkább.
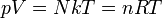
Van der Waals gáz/reális gáz
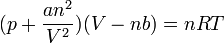 ahol a,b anyagi állandók, melyek rendre a gáz kölcsönhatásait, illetve a gázrészecskék méretét jellemzik.
ahol a,b anyagi állandók, melyek rendre a gáz kölcsönhatásait, illetve a gázrészecskék méretét jellemzik.
Fotongáz
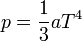
Speciális folyamatok ideális gázzal
Izoterm folyamat
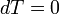
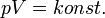
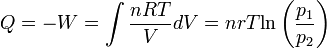
Izochor folyamat
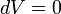
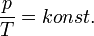
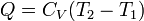
Izobár folyamat
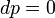
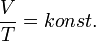
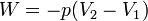

Adiabatikus folyamat
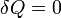
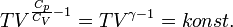
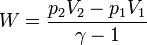
Politróp folyamat
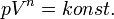
az előzők ennek spec. esetei
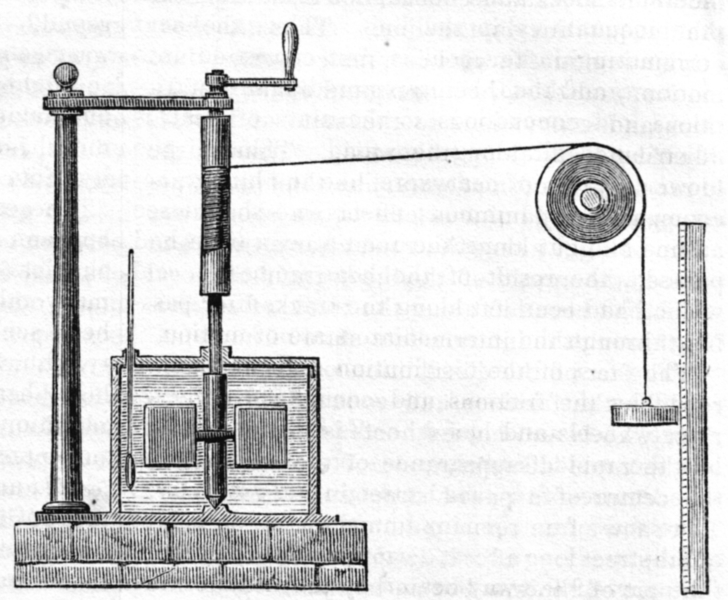
Joule-kísérlet
- Ez nem jó helyen van!
Joule egy higannyal töltött edényt lyukas falakkal részekre osztott. Az egyes térrészekben lapátok forogtak, a tengelyre helyezett tárcsa peremén ható forgatónyomaték hatására. A lapátok forgásba hozták a folyadékot, amely belső súrlódás folytán felmelegedett. Joule azt tapasztalta, hogy adiabatikus változás esetén ugyanakkora külső munka mindig ugyanakkora 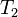 hőmérsékletre melegítette fel a folyadékot
hőmérsékletre melegítette fel a folyadékot 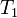 -ről.
-ről.
Reális gázok
Gay-Lussac kísérlet
A Gay-Lussac kísérletben egy adiabatikusan elzárt edényben lévő gázt egy elválasztó fal hirtelen kivételével hagyjuk szabadon tágulni. Ideális gáz hőmérséklete ekkor nem változna. A reális gázok viszont hűlnek.
Joule-Thomson kísérlet
A Joule-Thomson berendezés egy hőszigetelő henger, melynek két végén két mozgatható dugattyú van, középen pedig egy válaszfal. Kezdetben az egyik dugattyú a válaszfalnál van, a másik dugattyú és a válaszfal között pedig gáz van. Ezek után a gázt átpréseljük a válaszfalon, a vége az a dugattyú lesz a válaszfalnál, amelyik az előbb messze volt tőle, amelyik eredetileg közel volt, az pedig távol lesz. A hőszigetelő edény miatt hőátadás nincs:
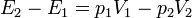
vagyis
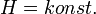
az entalpia megváltozása:
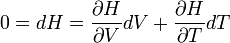
Innen
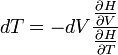
ez ideális gázra 0 lenne, ha viszont a gázrészecskék kölcsönhatásait is figyelembe vesszük(mint a VdW egyenlet), akkor a jelenség megérthető(a gáz melegedhet és hülhet is).
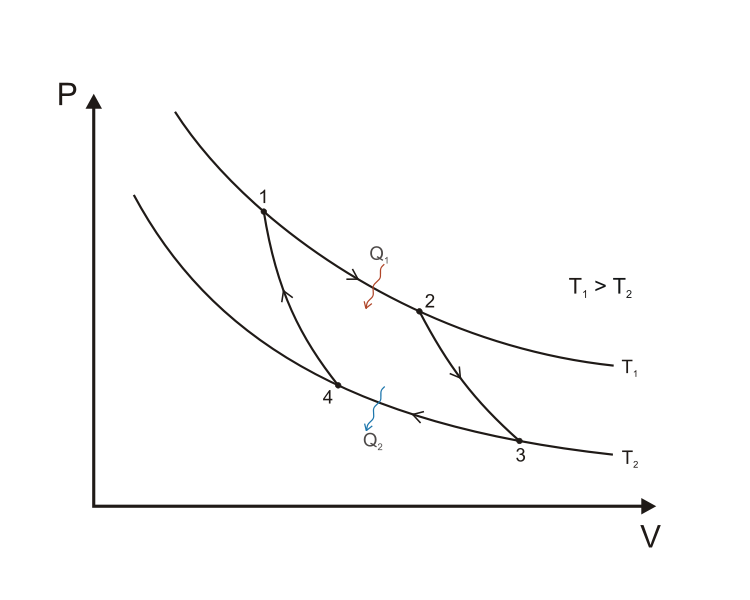
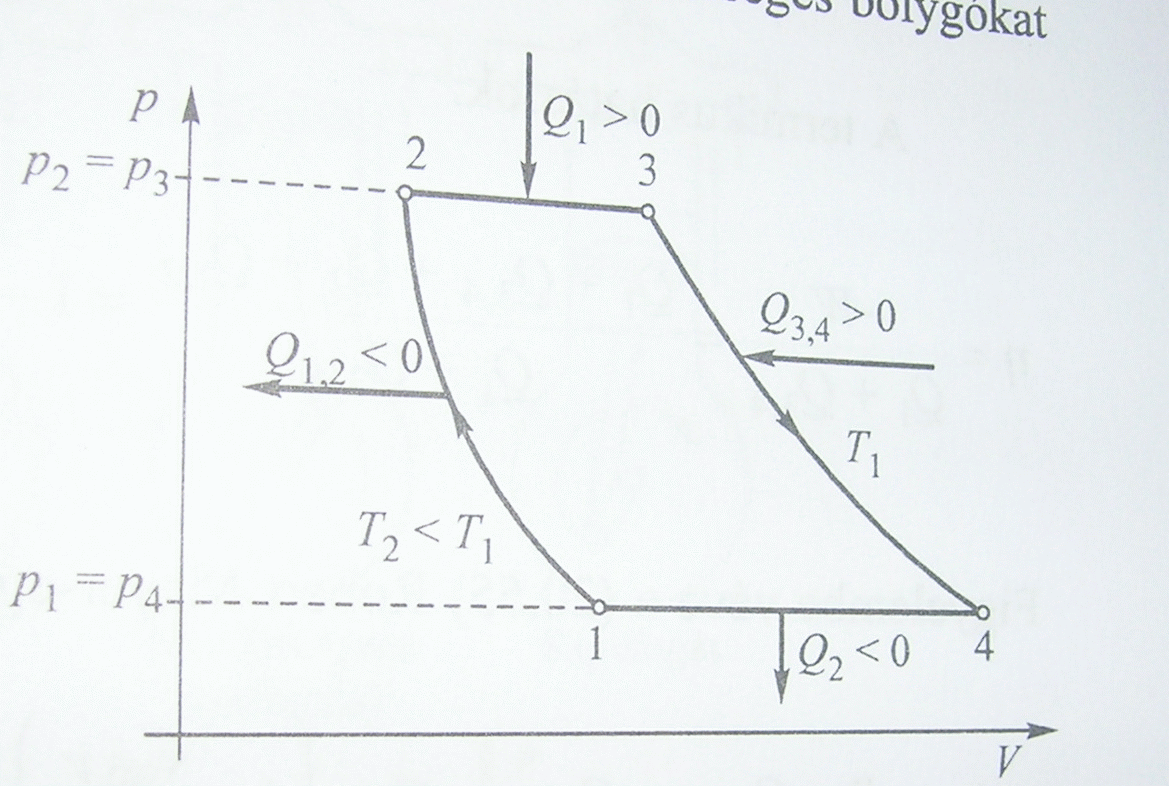
Carnot-körfolyamat
A folyamat szakaszai:
- 1-2 izoterm
- 2-3 adiabatikus
- 3-4 izoterm
- 4-1 adiabatikus
"Elméleti" megvalósítás:
1-es hőtartály 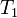 hőmérsékletű, innen vesz fel a hőerőgép
hőmérsékletű, innen vesz fel a hőerőgép 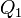 -et
2-es hőtartály
-et
2-es hőtartály 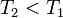 hőmérsékletű, ide ad le a hőerőgép
hőmérsékletű, ide ad le a hőerőgép 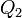 -t
-t
A Carnot-folyamat hatásfoka:
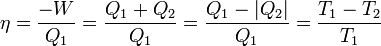
az utolsó egyenlőség ideális gázra érvényes.
Reverzibilis Carnot-folyamat: ellenkező irányba is végbemehet (hűtőgép, hőszivattyú modellje)
Az entrópia fogalma, második főtétel
A tapasztalat szerint a legtöbb termodinamikai folyamat nem megfordítható, vagyis irreverzibilis, ezen alapul a második főtétel.
Clausius féle megfogalmazás
Nem hozható létre olyan hőerőgép, amelyben a hő külső munkavégzés nélkül a hidegebb test felől a melegebb felé áramolna.
Kelvin féle megfogalmazás
Nem hozható semmilyen géppel sem olyan folyamat, amely során egy test hőt veszít és ez a hő 100%-os hatásfokkal munkává alakul.
A két megfogalmazás ekvivalenciája
fordított Carnot-gép + Kelvin-gép = Clausius-gép
direkt Carnot-gép + Clausius-gép = Kelvin-gép
Következmény reverzibilis Carnot-folyamatra nézve
A második főtétel egyik fontos következménye, hogy a reverzibilis Carnot-folyamat hatásfoka anyagi minőségtől független.
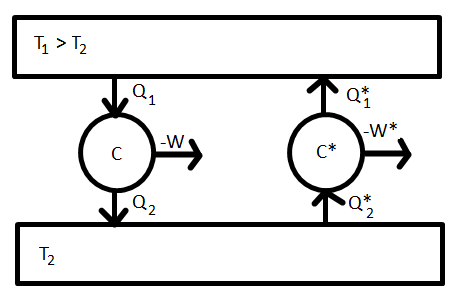
Biz.:Tekintsünk egy C direkt Carnot-gépet 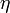 hatásfokkal és egy vele azonos hőtartályokból dolgozó C
hatásfokkal és egy vele azonos hőtartályokból dolgozó C fordított Carnot-gépet
fordított Carnot-gépet 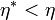 hatásfokkal. A C gép a
hatásfokkal. A C gép a 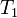 hőmérsékletű tartályból
hőmérsékletű tartályból 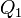 hőt von el,
hőt von el, 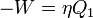 munkát végez, és
munkát végez, és 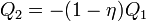 hőt ad le a
hőt ad le a 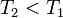 hőmérsékletű tartálynak. A C
hőmérsékletű tartálynak. A C gép beállításait válasszuk meg úgy, hogy a T_1 hőmérsékletű tartálynak éppen
gép beállításait válasszuk meg úgy, hogy a T_1 hőmérsékletű tartálynak éppen 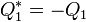 hőt adjon le. Ekkor C
hőt adjon le. Ekkor C gép
gép 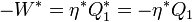 munkát végez, és a T_2 hőmérsékletű tartályból
munkát végez, és a T_2 hőmérsékletű tartályból 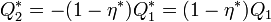 hőt vesz fel. A két gép együttes munkája ekkor
hőt vesz fel. A két gép együttes munkája ekkor 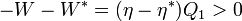 . Ellentmondásra jutottunk a második főtétellel, mert ez a végzett munka egyenlő e teljes hőfelvétellel. Hasonlóan beáltható, hogy
. Ellentmondásra jutottunk a második főtétellel, mert ez a végzett munka egyenlő e teljes hőfelvétellel. Hasonlóan beáltható, hogy 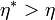 sem lehetséges. Az oldhatja fel az ellentmondást, ha
sem lehetséges. Az oldhatja fel az ellentmondást, ha 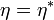 anyagi minőségtől függetlenül, így a korábban ideális gázokra írt hatásfok általánosan is helyes. Ezekszerint a reverzibilis Carnot-féle körfolyamatra a redukált hők összege nulla:
anyagi minőségtől függetlenül, így a korábban ideális gázokra írt hatásfok általánosan is helyes. Ezekszerint a reverzibilis Carnot-féle körfolyamatra a redukált hők összege nulla:
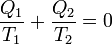
A termodinamikai hőmérsékleti skála
A reverziblis Carnot-folyamat hatásfokának anyagi minőségtől való függetlensége lehetővé teszi egy anyagi minősétől független termodinamikai hőmérsékleti skála definiálását. Két alappont(a víz forráspontja 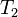 és a jég olvadáspontja
és a jég olvadáspontja 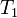 ) ismeretében készíthetünk egy Carnot-gépet, ennek hatásfoka megmérhető
) ismeretében készíthetünk egy Carnot-gépet, ennek hatásfoka megmérhető 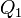 és
és 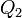 megmérésével. A két hőmérséklet különbségét Kelvin nyoimán 100 részre osztjuk. Ekkor:
megmérésével. A két hőmérséklet különbségét Kelvin nyoimán 100 részre osztjuk. Ekkor:
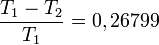
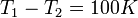
Ezek ismeretében 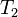 és ismeretlen T között a Q-k megmérésével meghatározott hatásfokból meghatározható a hőmérséklet:
és ismeretlen T között a Q-k megmérésével meghatározott hatásfokból meghatározható a hőmérséklet:
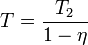
Irreverzibilis Carnot-körfolyamat
Természetesen az irreverziblis Carnot-körfolyamat hatásfoka a reverzibilisnél kisebb, következésképpen irreverzibilis Carnot-folyamatra:
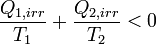
Clausius-egyenlőtlenség
Tetszőleges körfolyamat sok kicsi Carnot-folyamatra bontható, hiszen az ellentétes irányba mutató részek kiejtik egymást. Ebből következik, hogy tetszőleges folyamatra:
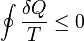
ahol az egyenlőség reverzibilis folyamat esetén áll fenn.
Az entrópia termodinamikai fogalma
Az, hogy 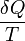 mennyiség körintegrálja reverzibilis folyamatra nulla, lehetővé teszi egy új, potenciál jellegű mennyiség bevezetését. Ez az entrópia:
mennyiség körintegrálja reverzibilis folyamatra nulla, lehetővé teszi egy új, potenciál jellegű mennyiség bevezetését. Ez az entrópia:
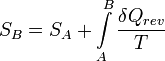
vagy differenciálisan:
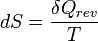
Ez a definíció csak egy additív konstans erejéig definiálja az entrópiát, az entrópiakonstans a kvantummechanika és a statisztikus fizika segítségével lesz majd kiszámítható. Ha tekintünk egy rendszert, amely A-ből B pontba irreverzibilis úton jut, illetve képzeletben jusson vissza A-ba reverzibilisen, ekkor a teljes körfolyamat is irreverzibilis:
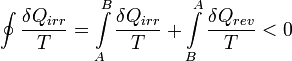
vagyis
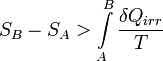
zárt rendszer esetén  ekkor irreverzibilis folyamatban a rendszer entrópiája csak nőhet, az egyensúly feltétele az entrópia maximuma.
ekkor irreverzibilis folyamatban a rendszer entrópiája csak nőhet, az egyensúly feltétele az entrópia maximuma.
A főtétel megfogalmazása az entrópia segítségével tehát:
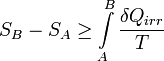
ahol az egyenlőség reverzibilis folyamatra teljesül.
A fundamentális egyenlet
Az első főtőtel:
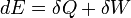
A második főtétel szerint
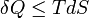
térfogati munka esetén:
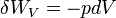
anyagtranszporthoz tartozó munka:
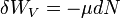
A fundamentális egyenlet:
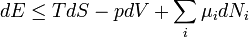
Legendre-transzformáció, termodinamikai potenciálok
Ahogy korábban az entalpia esetében láttuk, bizonyos problémákat érdemes a (belső) energia helyett más reprezentációban tárgyalni. Ez a termodinamika statisztikus alapozása szempontjából azt jelenti, hogy az egyes problémákhoz más-más sokaságot érdemes választani. A különböző reprezentációknak megfelelő termodinamikai potenciálok között matematikailag a Legendre-transzformáció teremt kapcsolatot.
| Energia | E |
| Entalpia | H=E+pV |
| Szabadenergia | F=E-TS |
| Szabadentalpia(Gibbs-potenciál) | G=E-TS+pV |
A megfelelő fundamentális egyenletek:
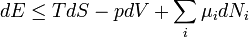
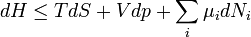
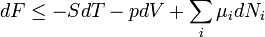
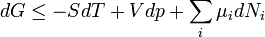
Szabadenergia
Izoterm-izochor egyensúlyba a szabadenergia minimális, ahogy az előző pont megfelelő egyelőtlenségéről leolvasható.
Izoterm esetben:
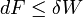
ahol W a rendszeren végzett munka. Így a szabadenergia a rendszerből kinyerhető maximális munkát méri. Reverzibilis izoterm folyamat esetén pedig a szabadenergia-változás jelentkezik munkaként.
Maxwell-relációk
A fundamentális egyenletek reverzibilis esetét véve(vagyis amikor egyenletek és nem egyenlőtlenségek), a Young-tételt alkalmazva, felírható pl.:

vagyis:
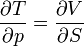
az ilyen alakú összefüggéseket Maxwell-relációknak nevezzük. Könnyen leolvashatók a potenciálok differenciáljaiból.
Szabadentalpia, kémiai affinitás
Izoterm-izobár egyensúlyban a rendszer szabadentalpiája minimális.
Izoterm-izobár folyamatokban a rendszeren végzett kémiai munka
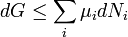
Izoterm-izobár reverzibilis folyamatban a szabadentalpia-változás alakul át munkává.
Izoterm-izobár egyensúly, kémiai reakciók
Legyenek a,b különböző fázisok, az anyagmegmaradás szerint:
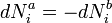
Ekkor a dG=0 egyensúlyi feltétel a következőt adja:
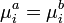
Önként végbemenő folyamatok szabadentalpia csökkenéssel járnak dG<0, eszerint a fázisból b fázisba akkor lesz átmenet, ha
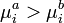
Hasonló módon, az, hogy egy kémiai reakció lejátszódik-e spontán, a szabadentalpia csökkenés előjelétől függ, nem a reakcióhőtől(entalpiaváltozástól) ahogy ezt régen tévesen hitték.
Az Euler-féle összefüggés, Gibbs-Duhem reláció
A homogén függvényekre érvényes Euler-tétel szerint:
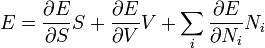
Innen:
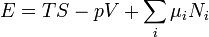
Ezt nevezik Euler-féle összefüggésnek. Ennek teljes differenciálja:
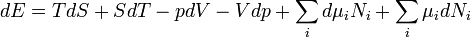
Ezt összevetve a fundamentális egyenlettel kapjuk a
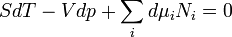
Gibbs-Duhem relációt.
Hőerőgépek
Gázturbina
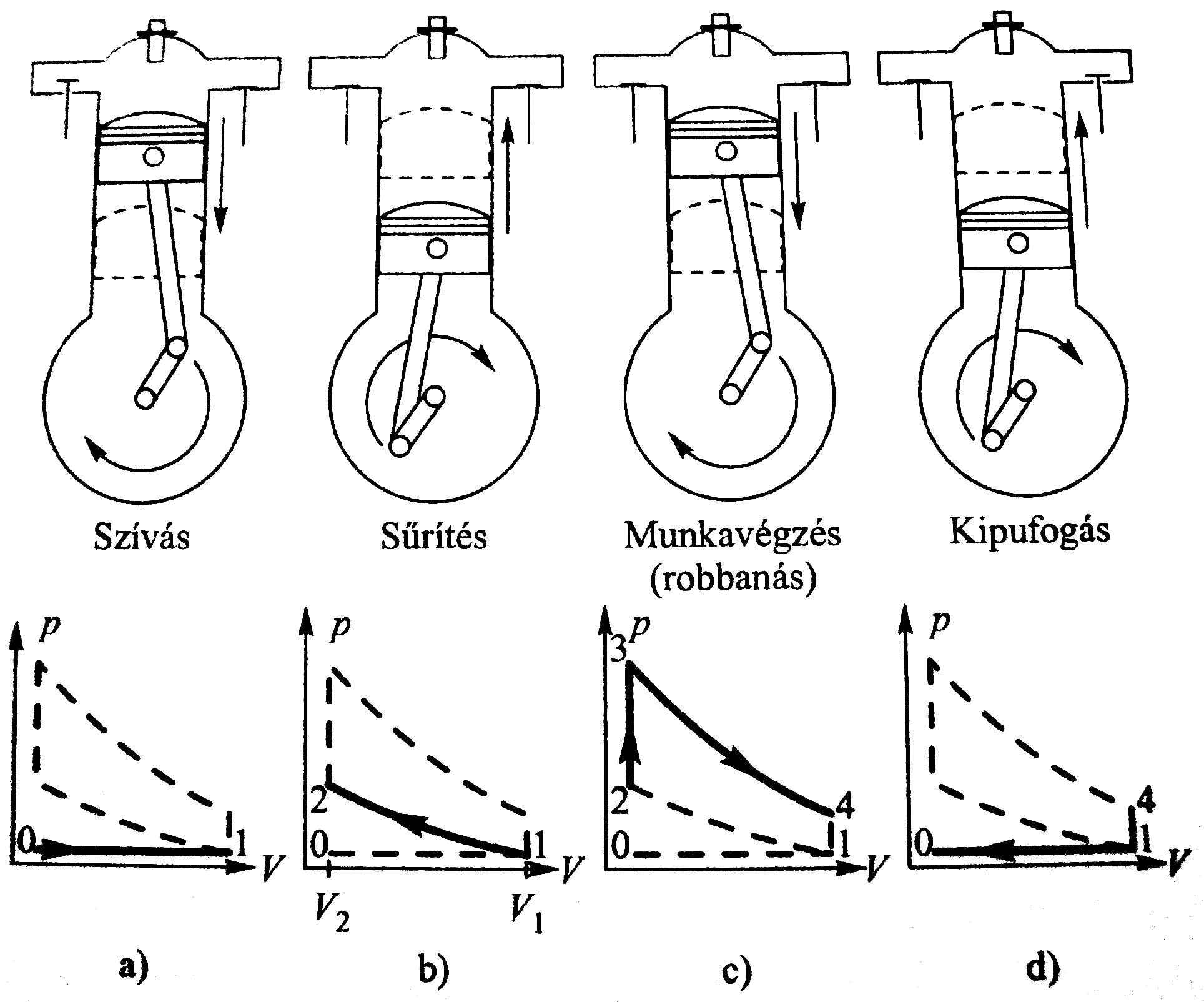
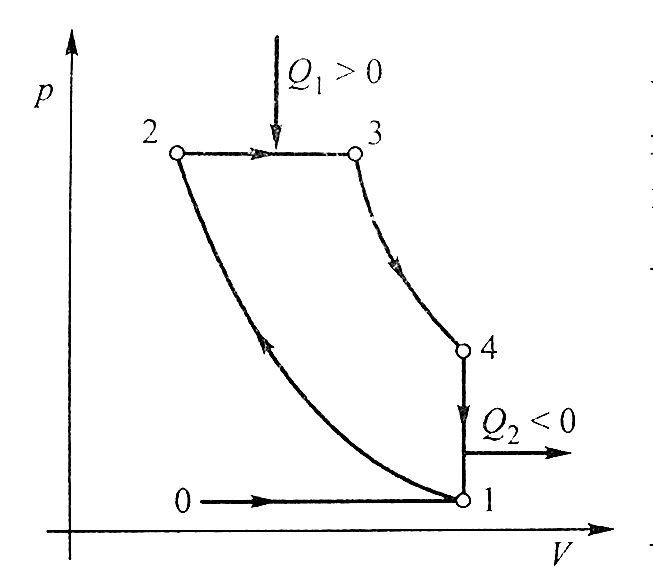
Otto-motor
Dízelmotor
Harmadik főtétel
A harmadik főtétel, vagy Nernst tétel kimondja, hogy 0K-en az anyagok entrópiája 0. Nernst alacsony hőmérsékleten és állandó nyomáson mért különböző galvánelem által termelt 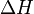 reakcióhőt, és
reakcióhőt, és 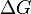 maximális hasznos munkát. Azt tapasztalta, hogy ezek 0K felé haladva egyre inkább megegyeznek. Planck erre támaszkodva kimutatta, hogy nemcsak
maximális hasznos munkát. Azt tapasztalta, hogy ezek 0K felé haladva egyre inkább megegyeznek. Planck erre támaszkodva kimutatta, hogy nemcsak 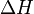 és
és 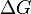 , de H és G is ugyanazon értékhez tartanak, méghozzá úgy, hogy 0K-en érintik egymást. Ezért:
, de H és G is ugyanazon értékhez tartanak, méghozzá úgy, hogy 0K-en érintik egymást. Ezért:
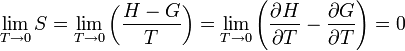
ahol a 0/0 típusú határétékre a L'Hospital szabályt alkalmaztuk.
A harmadik főtétel két fontos következménye:
- 0K-en az anyagok hőkapacitása 0

- A 0K hőmérséklet nem érhető el a gyakolatban
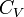 nagyon kicsi, ezért nagyon kis hőközlés is nagyon nagy felmelegedést okoz
nagyon kicsi, ezért nagyon kis hőközlés is nagyon nagy felmelegedést okoz
Alacsony hőmérsékletek előállítása
Hűtési módszerek:
- Hűtőkeverék alkalmazása
- Párolgás
- Indirekt Carnot-gép
- Gázok lehűtése tágulással
- Adiabatikus lemágnesezés
Lényeg: A külső mágneses tér eltávolításakor a termikus entrópia mágneses entrópiává válik(a mágneses momentumok rendezetlenségévé).
Fázisátalakulások termodinamikai tárgyalása
Általánosan
Először azt látjuk be, hogy egyensúly esetén a G szabadentalpia konkáv függvénye T-nek és p-nek, az F szabadenergia pedig konvex függvénye V-nek és konkáv függvénye T-nek. Az első deriváltak:
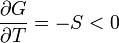
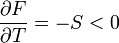
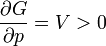
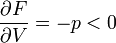
A második deriváltak:
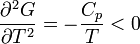
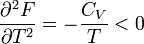
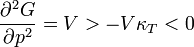
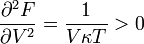
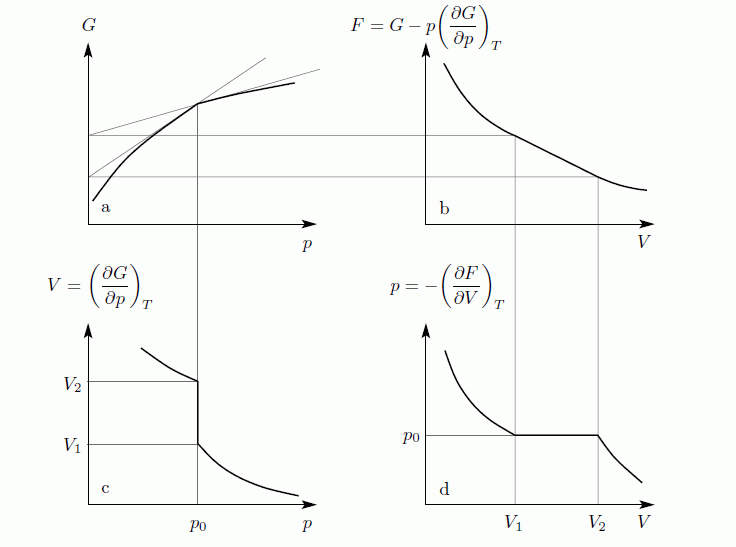
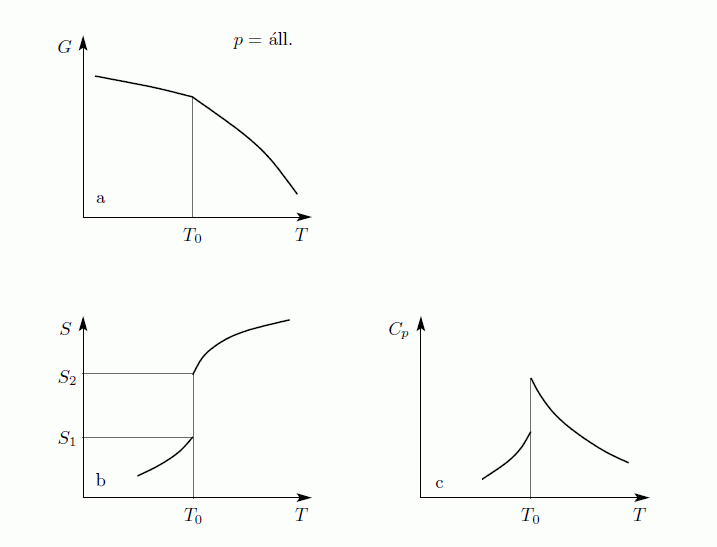
Amit be akartunk látni. G-ről és F-ről tudjuk, hogy folytonosak, de a deriváltjaik rendelkezhetnek szingularitásokkal. Először nézzük azt az esetet, amikor az első deriváltnak szakadása van, vagyis a térfogat 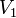 -ről
-ről 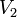 -re ugrik. Tegyük fel, hogy állandó hőmérsékleten G szakadással rendelkezik
-re ugrik. Tegyük fel, hogy állandó hőmérsékleten G szakadással rendelkezik 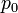 -ban. G ismeretében F már megkapható, hiszen:
-ban. G ismeretében F már megkapható, hiszen:
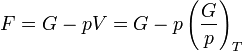
Az így kapott görbék konzisztensek az egyensúlyi feltételekkel. Ekkor a 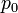 pontban a rendszer adott paraméterekkel rendelkező állapotából egy erősen különböző állapotba kerül. Általában fázisátalakulásról beszélünk, ha a termodinamikai potenciálok nem analitikus függvények. Ha az első derivált nem folytonos, akkor elsőrendű fázisátalakulásról, ha a második derivált nem folytonos, akkor másodrendű fázisátalakulásról beszélünk. Az előző ábrán szemléltetett fázisátalakulás elsőrendű. Általában rögzített p esetén is van olyan
pontban a rendszer adott paraméterekkel rendelkező állapotából egy erősen különböző állapotba kerül. Általában fázisátalakulásról beszélünk, ha a termodinamikai potenciálok nem analitikus függvények. Ha az első derivált nem folytonos, akkor elsőrendű fázisátalakulásról, ha a második derivált nem folytonos, akkor másodrendű fázisátalakulásról beszélünk. Az előző ábrán szemléltetett fázisátalakulás elsőrendű. Általában rögzített p esetén is van olyan 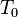 , ahol G-nek törése van, azaz az első derivált ugrás szerűen változik. Az első derivált az entrópia, ezért
, ahol G-nek törése van, azaz az első derivált ugrás szerűen változik. Az első derivált az entrópia, ezért 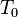 hőmérsékleten
hőmérsékleten 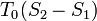 látens hő szabadul fel/nyelődik el. Ez az elsőrendű fázisátalakulások jellemző tulajdonsága. Elsőrendű fázisátmenet a forrás, a fagyás, és a szilárd testek szerkezetváltozásainak nagyrésze.
látens hő szabadul fel/nyelődik el. Ez az elsőrendű fázisátalakulások jellemző tulajdonsága. Elsőrendű fázisátmenet a forrás, a fagyás, és a szilárd testek szerkezetváltozásainak nagyrésze.
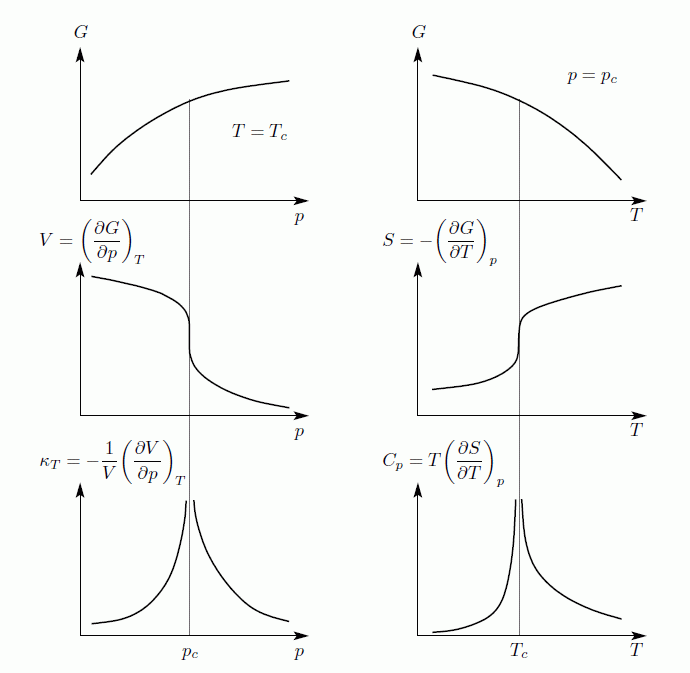
Másodrendű fázisátalakulásulások esetén előfordul, hogy az első deriváltaknak törése van, vagyis a második derivált ugrik(pl. szupravezető anyagok fajhőjében), de sokkal gyakoribb, hogy az első deriváltnak függőleges érintőjű inflexiós pontja van, így a második deriváltak divergálnak. Másodrendű átalakulás esetén az átalakulási pontot kritikus pontnak(illetve 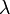 -pontnak) szokták nevezni. A már említetten kívül másodrendű fázisátalakulás például a hélium folyadék-szuperfolyadék átmenete.
-pontnak) szokták nevezni. A már említetten kívül másodrendű fázisátalakulás például a hélium folyadék-szuperfolyadék átmenete.
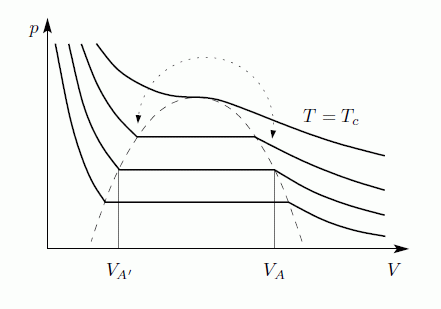
A folyadék-gáz átalakulás a VdW egyenlet alapján
A VdW egyenlet egy mol anyagra:
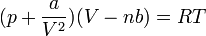
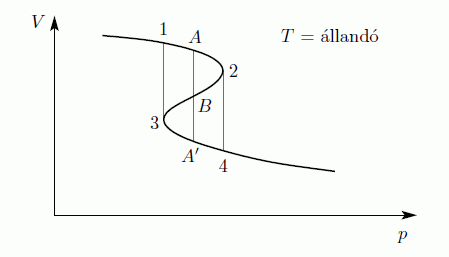
Először tegyük fel, hogy az egyenlet alacsony hőmérsékleten is homogén rendszert ír le. Ekkor a V-p diagram:
AA' szakaszt úgy definiáljuk, hogy A2B és B3A' területek megegyezzenek. A Gibbs-Duhem relációból állandó hőmérséklet esetén
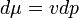
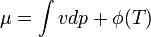
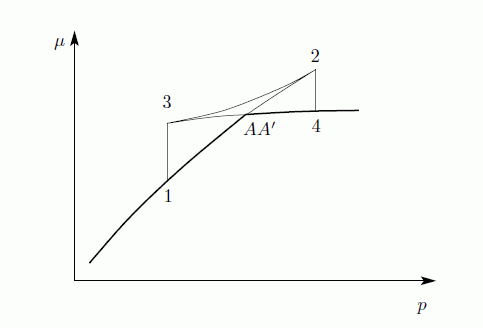
Az integrál vázlatosan így néz ki a felső határa függvényében:
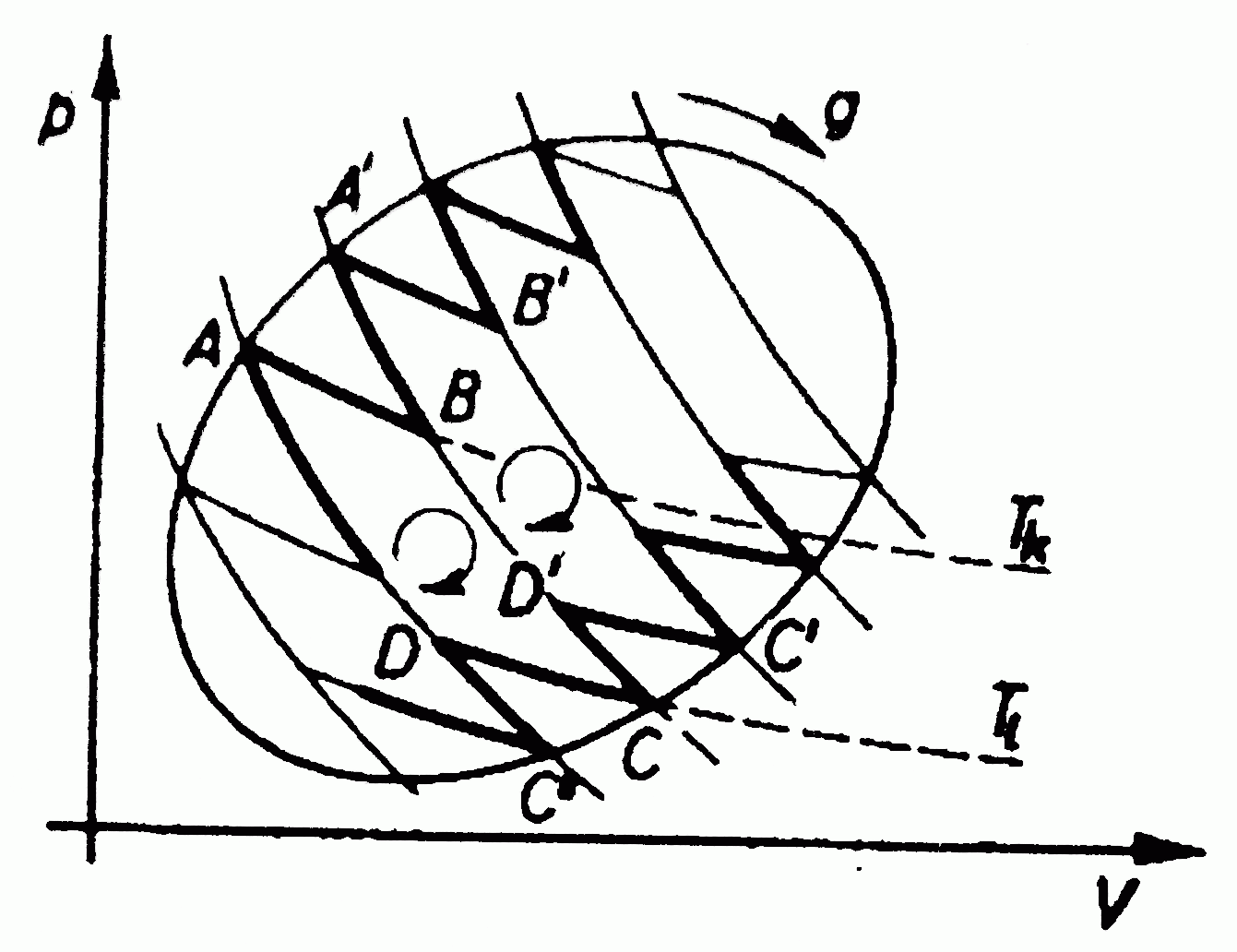
Az egyensúly feltétele G minimuma, ezért A23A' nem valósul meg, csak a vastagon húzott rész. A rendszer tehát AA' szakaszon marad egészen addig amíg A'-ig nem ér. Ekkor a rendszer nem lehet homogén, és nem is a VdW egyenlet írja le, hanem az, hogy G minimális. Ez a Maxwell-konstrukció:
Az egyenes vonalaknál tehát a rendszer nem lehet homogén, itt elsőrendű fázisátalakulás van. Megmutatható továbbá, hogy a 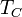 pontban a fázisátalakulás másodrendű.
pontban a fázisátalakulás másodrendű.
Fázisegyensúlyok
Gibbs féle fázisszabály
K - kémiailag egységes anyagok/komponensek száma
Sz - szabadsági fokok száma(pl.: a víz hármaspontjánál a szabadsági fokok száma 0, a vízgőz szabadsági fokainak száma 2, mert a nyomást és a hőmérsékletet lehet valamennyire változtatni anélkül, hogy új fázis keletkezne)
F - fázisok száma
N - külső állapotjelzők száma
A Gibbs-féle fázisszabály kimondja, hogy
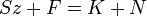
Biz.:Az egyensúlyi állapot jellemzéséhez ismernünk kell az N külső állapotjelzőt(pl. nyomás, hőmérséklet), illetve a fázisok n_i összetéltelét(hiszen a külső paraméterek és a kémiai potenciálok egyensúlyban egyenlőek a fázisokra). Egy fázis összetételét K-1 adattal(pl. K-1 móltörttel) adhatjuk meg. Az összetételt jellemző változók száma tehát F(K-1). Az öszes független intenzív változók száma F(K-1)+N. A kémiai potenciálok között felírható K(F-1) független összefüggés. Innen Sz=F(k-1)+N-K(F-1)=K-F+N.
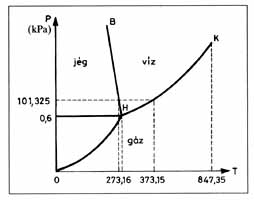
Fázisdiagramok
A képen a víz fázisdiagramja látható. Ez annyiból nem szokványos, hogy a szilárd-folyadék fázisegyensúlyt jelző görbe deriváltja negatív. Megfigyelhető a kritikus pont (K), amely felett nincs fázisátalakulás a folyadék és a gáz között, nem alkotnak külön fázist, ez a szuperkritikus folyadék tartomány.
Clausius-Clapeyron egyenlet
A Clausius Clapeyron egyenlet írja le kétfázisú rendszerek egyensúlyának feltételét. A szabadentalpia:
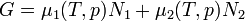
A részecskeszám megmaradás miatt 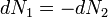 , akkor az egyensúly DG=0 feltételéből visszakapjuk a korábban is említett
, akkor az egyensúly DG=0 feltételéből visszakapjuk a korábban is említett 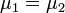 feltételt. Ebből az egy mólnyi mennyiségre vonatkozó
feltételt. Ebből az egy mólnyi mennyiségre vonatkozó 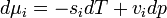 Gibbs-Duhem reláció adja a Clausius-Clapeyron egyenletet:
Gibbs-Duhem reláció adja a Clausius-Clapeyron egyenletet:
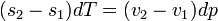
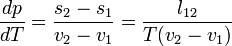
ahol v moláris térfogat, s moláris entrópia, 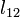 moláris látens hő.
moláris látens hő.