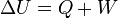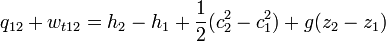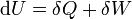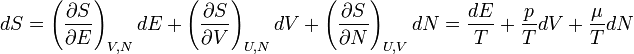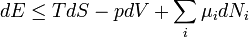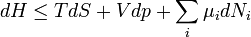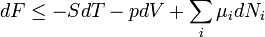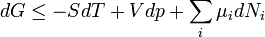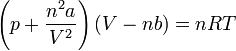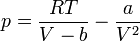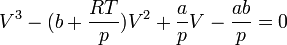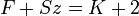„Fenomenologikus termodinamika” változatai közötti eltérés
(→Fázisdiagramok) |
(→Clausius-Clapeyron egyenlet) |
||
| (7 közbenső módosítás ugyanattól a szerkesztőtől nincs mutatva) | |||
| 37. sor: | 37. sor: | ||
==Nyílt és zárt folyamatok== | ==Nyílt és zárt folyamatok== | ||
| − | + | '''Nyílt rendszer''' | |
| − | |||
| − | + | A nyílt rendszerek jellemzője az [[anyag]] és az [[energia]] áramlása a rendszer és környezete között. | |
| − | |||
| − | + | Ilyen például egy pohár lefedetlen víz. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===Carnot-folyamat=== | ===Carnot-folyamat=== | ||
| 107. sor: | 97. sor: | ||
=== III. főtétel === | === III. főtétel === | ||
| − | Nernst megfogalmazása szerint az abszolút tiszta kristályos anyagok [[entrópia|entrópiája]] nulla kelvin hőmérsékleten zérus. | + | [[Nernst]] megfogalmazása szerint az abszolút tiszta kristályos anyagok [[entrópia|entrópiája]] nulla kelvin hőmérsékleten zérus. |
| − | Olyan abszolút tiszta kristályos anyag, amelyre a Nernst megfogalmazása érvényes lenne, a természetben nem fordul elő, ideális fogalom, tehát nulla entrópiájú anyag nem létezhet. Az entrópia határértékét a harmadik főtétel pontosított megfogalmazása a következőképpen rögzíti: a termodinamikai rendszerek entrópiája véges pozitív érték felé, az entrópia hőmérséklet szerinti deriváltja pedig a zéró felé tart, amikor a rendszer hőmérséklete az abszolút nulla érték felé közelít. | + | Olyan abszolút tiszta kristályos anyag, amelyre a Nernst megfogalmazása érvényes lenne, a természetben nem fordul elő, ideális fogalom, tehát nulla entrópiájú anyag nem létezhet. Az [[entrópia]] határértékét a harmadik főtétel pontosított megfogalmazása a következőképpen rögzíti: a termodinamikai rendszerek entrópiája [[véges]] pozitív érték felé, az entrópia hőmérséklet szerinti deriváltja pedig a zéró felé tart, amikor a rendszer hőmérséklete az abszolút nulla érték felé közelít. |
Nernst posztulátumát később egy újabb megfogalmazásban hozta nyilvánosságra, mely szerint az abszolút nulla hőmérséklet tetszőlegesen megközelíthető, de nem érhető el. E kijelentés a harmadik főtétel előbbi megfogalmazásának következménye: mivel az abszolút nullához közeli hőmérsékleten az anyagok fajhője nagyon kicsi, igen kis hőmennyiség a hőmérséklet jelentős megváltozásához vezet. Bármilyen módon is valósítjuk meg a hűtést, a lehűtendő test valamilyen fokú visszamelegedése elkerülhetetlen. A folyamat megismétlésével a hőmérséklet tovább csökkenthető, tehát végső soron az abszolút nulla hőmérséklet elvileg tetszőleges pontossággal aszimptotikusan megközelíthető, de nem érhető el. | Nernst posztulátumát később egy újabb megfogalmazásban hozta nyilvánosságra, mely szerint az abszolút nulla hőmérséklet tetszőlegesen megközelíthető, de nem érhető el. E kijelentés a harmadik főtétel előbbi megfogalmazásának következménye: mivel az abszolút nullához közeli hőmérsékleten az anyagok fajhője nagyon kicsi, igen kis hőmennyiség a hőmérséklet jelentős megváltozásához vezet. Bármilyen módon is valósítjuk meg a hűtést, a lehűtendő test valamilyen fokú visszamelegedése elkerülhetetlen. A folyamat megismétlésével a hőmérséklet tovább csökkenthető, tehát végső soron az abszolút nulla hőmérséklet elvileg tetszőleges pontossággal aszimptotikusan megközelíthető, de nem érhető el. | ||
| 186. sor: | 176. sor: | ||
===Fázisdiagramok=== | ===Fázisdiagramok=== | ||
| − | [[Fájl: | + | [[Fájl:viz.jpg|bélyegkép|jobbra|300px|A víz fázisdiagramja. A képen a víz fázisdiagramja látható. Ez annyiból nem szokványos, hogy a szilárd-folyadék fázisegyensúlyt jelző görbe deriváltja negatív.]] |
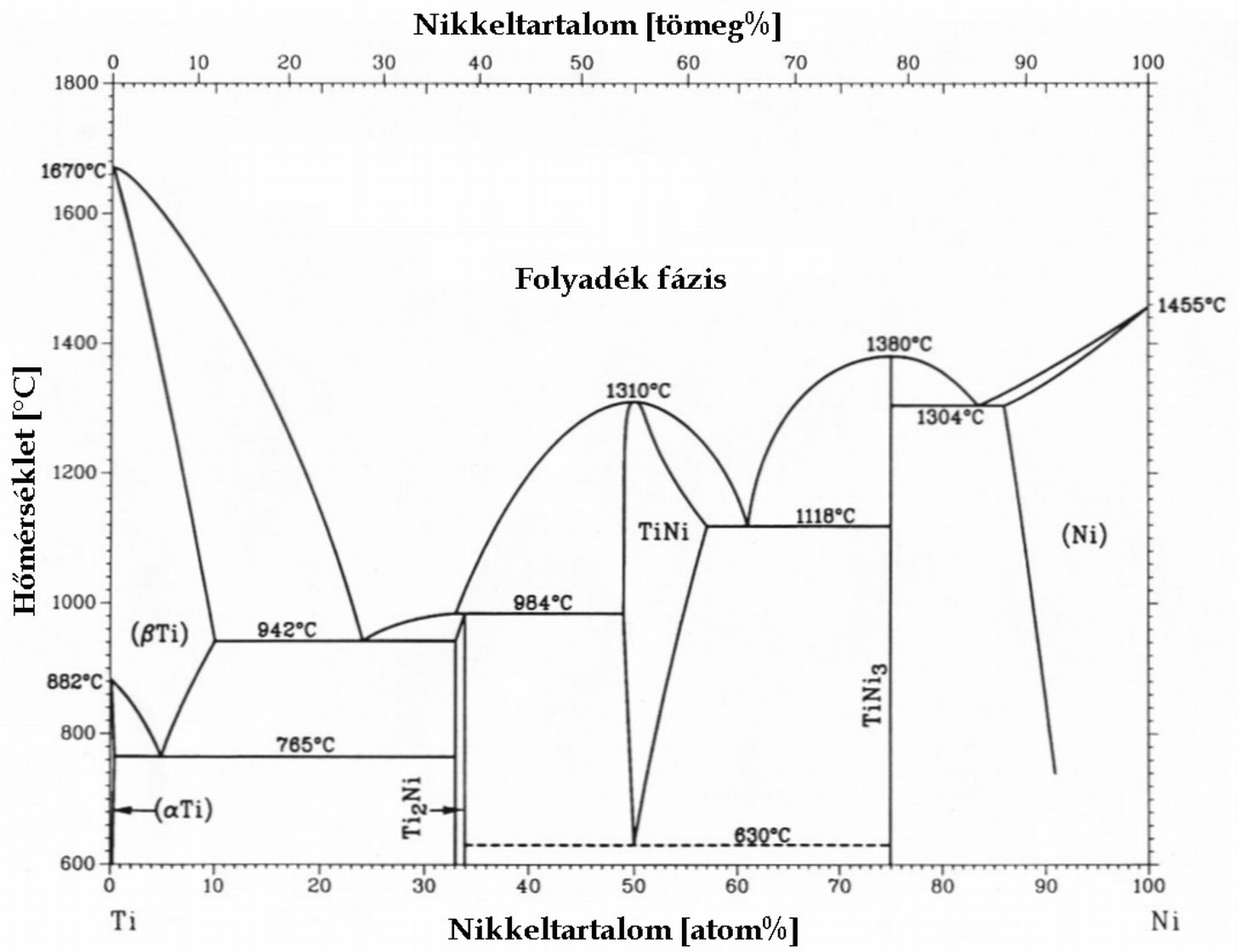
| − | [[Fájl:Titan_nikkel_fazisdiagram.jpg|bélyegkép|balra|300px|A titán-nikkel ötvözet fázisdiagramja]] | + | Az olyan diagramot, amit fázisok szerinti tartományokra osztunk fel, '''fázisdiagramnak''' nevezzük. A tengelyeken legtöbbször két választott változó, pl. p-T felmérése mellett, ilyenkor a többi változót rögzítjük. Szemléletesen: a teljes teret egy síkkal metsszük el. Az ábrákon a víz nyomás-hőmérséklet fázisdiagramja és a titán nikkel ötvözetek hőmérséklet-koncentráció diagramja látható. |
| + | [[Fájl:Titan_nikkel_fazisdiagram.jpg|bélyegkép|balra|300px|A titán-nikkel ötvözet fázisdiagramja jó példa a többkomponensű rendszerek bonyolultságára]] | ||
| + | |||
| + | A folyadék és légnemű fázisok közötti minőségi különbség megszűnik a kritikus pontnál (''K''). A kritikus pont felett a folyadékból folytonosan lesz légnemű anyag. Folyadékállapotból légneműbe fázisátalakulás nélkül is eljuthatunk a kritikus pont megkerülésével. | ||
| + | {{-}} | ||
==Kémiai potenciál== | ==Kémiai potenciál== | ||
| + | A '''kémai potenciál''' más néven parciális szabadentalpia, parciális [[Gibbs szabadentalpia|Gibbs-energia]] a rendszer alkotóira jellemző mennyiség. | ||
| + | |||
| + | A kémiai potenciált definiáló összefüggés: | ||
| + | |||
| + | :<math>\mu_\mathrm{i}=\left( \frac{\partial G}{\partial {N_\mathrm i}}\right)_{p,T,N_\mathrm{j\ne i}},\ \left[\mathrm {J}\right]</math> , | ||
| + | :ahol | ||
| + | :''G'' a rendszer Gibbs-energiája, [J] | ||
| + | :''N''<sub>''i''</sub> az ''i'' komponenst alkotó atomok száma, [1] | ||
| + | :''p'' a nyomás, [Pa] | ||
| + | :''T'' a hőmérséklet, [K]. | ||
| + | |||
| + | Az ''i'' [[komponens]] kémiai potenciálja egy [[Termodinamikai állapotjelzők#Intenzív állapotjelzők|intenzív fizikai mennyiség]], ami megadja, hogy az ''i'' komponens változása esetén mennyivel változtatja meg a rendszer szabadentalpiáját, azaz az integrális mennyiségét (miközben a rendszerben a hőmérséklet, a nyomás és az ''i'' komponens kivételével az összes többi komponens mennyisége állandó marad). A kémiai potenciál abszolút értéke nem ismeretes, gyakorlatban a folyamatokban bekövetkező megváltozása fontos. | ||
==Fázisegyensúlyok== | ==Fázisegyensúlyok== | ||
| + | ===Clausius-Clapeyron egyenlet=== | ||
| + | A Clausius Clapeyron egyenlet írja le kétfázisú rendszerek egyensúlyának feltételét. A szabadentalpia: | ||
| + | |||
| + | <math>G=\mu_1(T,p) N_1 +\mu_2(T,p) N_2\,</math> | ||
| + | |||
| + | A részecskeszám megmaradás miatt <math>dN_1=-dN_2</math>, akkor az egyensúly ''dG=0'' feltételéből visszakapjuk a korábban is említett <math>\mu_1=\mu_2</math> feltételt. Ebből az egy mólnyi mennyiségre vonatkozó <math>d\mu_i=-s_idT + v_idp</math> [[Gibbs-Duhem reláció]] adja a Clausius-Clapeyron egyenletet: | ||
| + | |||
| + | <math>(s_2-s_1)dT=(v_2-v_1)dp\,</math> | ||
| + | |||
| + | <math>\frac{dp}{dT}=\frac{s_2-s_1}{v_2-v_1}=\frac{l_{12}}{T(v_2-v_1)}</math> | ||
| + | |||
| + | ahol v moláris térfogat, s moláris [[entrópia]], <math>l_{12}</math> moláris [[látens hő]]. | ||
==Jegyzetek, hivatkozások== | ==Jegyzetek, hivatkozások== | ||
<references/> | <references/> | ||
| + | |||
| + | {{Záróvizsga}} | ||
A lap jelenlegi, 2011. június 26., 10:41-kori változata
A tétel korábbi változata megtekinthető a Fenomenologikus termodinamika (2010) címszó alatt. Kevésbé struktúrált, de részletesebb, mint az új.
Tartalomjegyzék
Termodinamikai állapotjelzők
Az állapotjelző a termodinamikai rendszernek egy olyan jellemzője, amely csak a rendszer állapotától függ, és nem függ attól, hogyan jutott a rendszer ebbe az állapotba. Az állapotjelző a rendszer egyensúlyi állapotát írja le. Például a belső energia, az entalpia, entrópia, nyomás és hőmérséklet állapotjelzők, mivel kvantitatíve jellemzik egy termodinamikai rendszer egyensúlyi állapotát. Ugyanakkor a mechanikai munka és a hő nem állapotjelző, mivel kvantitatíve a termodinamikai rendszerek egyensúlyi állapotai közötti átmeneteket írják le. Megkülönböztetünk intenzív és extenzív állapotjelzőket.
Hőtágulás
Hőtágulásnak nevezzük azt a fizikai jelenséget, amikor valamely anyag a hőmérsékletének változásával megváltoztatja a méretét. Melegítéskor az anyagok általában tágulnak, a tágulás relatív mértékét a hőtágulási együttható fejezi ki. A hőtágulás általában közelítőleg lineárisan függ a hőmérséklettől, ez alól kivétel, ha halmazállapot-változás történik, illetve néhány speciális, vagy bomlékony anyag zsugorodik (negatív hőtágulás). Léteznek kerámiák és fémötvözetek, amelyek gyakorlatilag nem változtatják a méretüket.
A lineáris hőtágulási együttható a szilárd anyag hőmérséklet változásra adott hosszméret változásának a mértéke:
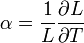 [K-1]
[K-1]
A térfogati hőtágulási együttható az anyagok termodinamikai tulajdonsága, melyet az alábbi összefüggéssel definiálnak[1]:
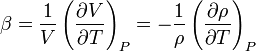 [K-1]
[K-1]
ahol 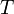 a hőmérséklet,
a hőmérséklet, 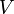 a térfogat,
a térfogat, 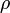 a sűrűség, a deriválást állandó nyomás mellett hajtják végre; β pedig a sűrűség változásának mértéke állandó nyomáson, a hőmérsékletváltozás hatására.
a sűrűség, a deriválást állandó nyomás mellett hajtják végre; β pedig a sűrűség változásának mértéke állandó nyomáson, a hőmérsékletváltozás hatására.
Ideális gáz, kinetikus modell
A gázok törvényszerűségei leírhatók a mozgó testekre vonatkozó fizikai törvényekkel, ha feltételezzük ideális voltukat, amihez a következő kritériumoknak kell teljesülniük:
- A gázmolekulák saját térfogata elhanyagolható a gáz által betöltött térfogathoz képest
- A gázmolekulák egymásra sem vonzó, sem taszító hatást nem fejtenek ki, az ütközésektől eltekintve
- A gázmolekulák egymással illetve az edény falával való ütközése rugalmas
- A gázmolekulák átlagos sebességét és kinetikai energiáját a gáz hőmérséklete adja meg
- Azonos hőmérsékleten, azonos számú gázmolekula kinetikai energiája megegyezik, és független a gáz anyagi minőségétől
Az ideális gázokra, és csak az ideális gázokra teljesül az egyesített gáztörvény.
Általában számításoknál a gázokat – első közelítésben – ideális gázoknak tekintjük. A légnemű közegek jellemzően akkor közelítik meg a tökéletes gázokra jellemző tulajdonságokat, ha hőmérsékletük kritikus hőmérsékletüknél nagyobb (ahol a párolgáshő nulla). Azokat a légnemű anyagokat, amelyeknek hőmérséklete a kritikus hőmérséklet alatti, gőznek hívjuk.
Nyílt és zárt folyamatok
Nyílt rendszer
A nyílt rendszerek jellemzője az anyag és az energia áramlása a rendszer és környezete között.
Ilyen például egy pohár lefedetlen víz.
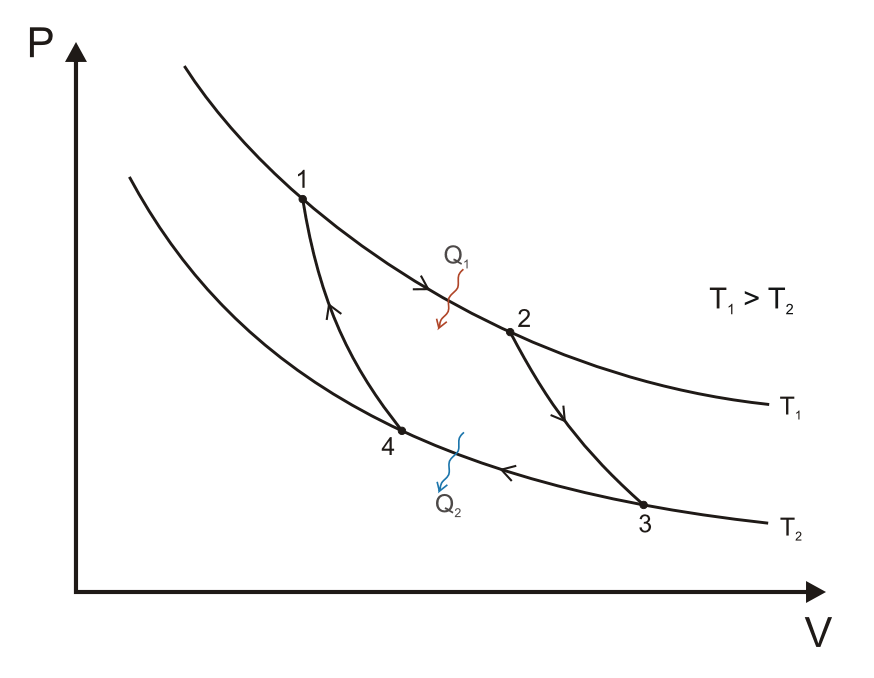
Carnot-folyamat
A Carnot körfolyamat, ha hőerőgépként működik, négy állapotváltozásból áll:
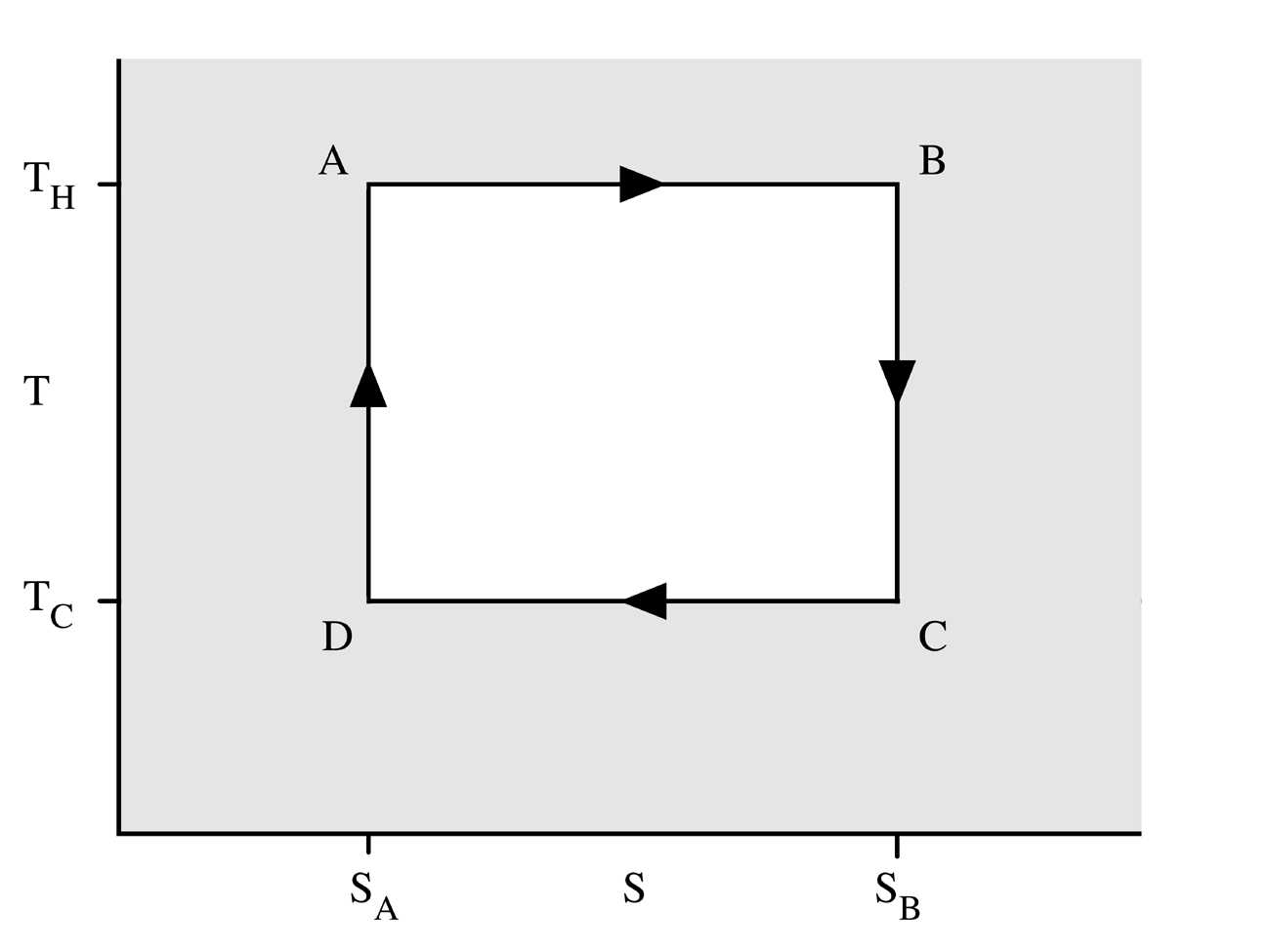
- A gáz reverzibilis izoterm tágulása (expanziója) a TH[2] nagyobb hőmérsékleten (izoterm hőközlés). Ez alatt az állapotváltozás alatt (Az 1. ábrán A állapotból B állapotba) a táguló gáz munkát végez a dugattyún. A gáz tágulását a nagy hőmérsékletű tartályból beáramló hő okozza.
- Izentrópikus (reverzibilis adiabatikus) tágulás. Ennél az állapotváltozásnál (B-ből C-be) feltesszük, hogy a henger és a dugattyú hőszigetelt: nem kap, és nem is veszít hőt a rendszer. A gáz tovább tágul, munkát végezve a környezetén. Ennek eredményeképp a gáz a hidegebb TC[3] hőmérsékletre hűl.
- Reverzibilis izotermikus összenyomódás (sűrítés, kompresszió) a TC hideg hőmérsékleten (izoterm hőleadás). (C-ből D-be). Ekkor a környezet végez munkát a gázon, miközben hő áramlik a gázból a hideg tartályba.
- A gáz izentrópikus összenyomódása. (D-ből A-ba) Ismét felételezzük, hogy a dugattyú és a henger hőszigetelt. A környezet végez munkát a gázon miközben összenyomja azt, ezáltal a hőmérsékletét TH-ra emelve. Az állapotváltozás végén a gáz a kiindulási állapotba jut vissza.
Főtételek
0. főtétel: a termodinamikai rendszer egyensúlya
A nulladik főtétel tulajdonképpen nem egyetlen "törvényt", hanem több posztulátumot jelent, amelyek a termodinamikai rendszer egyensúlyával kapcsolatosak. Ezek:
- bármely magára hagyott termodinamikai rendszer egy idő után egyensúlyi állapotba kerül amelyből önmagától nem mozdulhat ki;
- egy egyensúlyban levő termodinamikai rendszer szabadságfokainak száma a környezetével megvalósítható kölcsönhatások számával egyenlő;
- a két testből álló magára hagyott termodinamikai rendszer egyensúlyban van, ha a testek között fellépő kölcsönhatásokat jellemző intenzív állapothatározóik egyenlők;
- az egyensúly tranzitív (ha A rendszer termodinamikai egyensúlyban van C rendszerrel és B rendszer is termodinamikai egyensúlyban van C rendszerrel, akkor ebből következik, hogy A és B rendszer is termodinamikai egyensúlyban van egymással).
I. főtétel – Energiamegmaradás törvénye
A termodinamika első főtétele mennyiségi összefüggést állapít meg a mechanikai munka, a cserélt hő és a belső energia változása között.
Egy nyugvó és zárt termodinamikai rendszer belső energiáját, amennyiben annak belsejében nem zajlik le fázisátalakulás vagy kémiai reakció, kétféleképpen lehet megváltoztatni: munkavégzéssel és hőközléssel. A rendszer 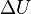 belső energiájának megváltozása tehát a vele közölt Q hőmennyiség és a rajta végzett W (bármilyen) munka összege:
belső energiájának megváltozása tehát a vele közölt Q hőmennyiség és a rajta végzett W (bármilyen) munka összege:
Áramló közegre a hő és a technikai munka összege így számolható:
ahol q a hő, w(t12) a technikai munka, h az entalpia, c a közegáramlás sebessége, g a gravitációs állandó, és z a vizsgált pont magassága (helyzete). Differenciális alakban:
Következménye: Nincs olyan periodikusan működő gép, ú.n. elsőfajú perpetuum mobile (örökmozgó), mely hőfelvétel nélkül képes lenne munkát végezni.
II. főtétel
A második főtétel a spontán folyamatok irányát szabja meg. Több, látszólag lényegesen különböző megfogalmazása van.
- Clausius-féle megfogalmazás (1850.): A természetben nincs olyan folyamat, amelyben a hő önként, külső munkavégzés nélkül hidegebb testről melegebbre menne át. Csakis fordított irányú folyamatok lehetségesek.
- Kelvin-Planck-féle megfogalmazás (1851., 1903.): A természetben nincs olyan folyamat, amelynek során egy test hőt veszít, és ez a hő munkává alakulna át. Szemléletesen egy hajó lehetne ilyen, amelyik a tenger vizéből hőenergiát von el és a kivont hőenergiával hajtja magát. Ez nem mond ellent az energiamegmaradásnak, mégsem kivitelezhető.
Az ilyen gépet másodfajú perpetuum mobilének nevezzük, tehát az állítás szerint nem létezik másodfajú perpetuum-mobile.
A két megfogalmazás egymásból következik, de a levezetése nem teljesen egyszerű.
A második alaptörvénynek ezek és az ezekhez hasonló megfogalmazásai zavarbaejtőek, hiszen a fizika többi, összefüggéseket megállapító törvényeivel szemben valaminek a létezését tagadják. Egy jobb megfogalmazás végett egy új fogalom került bevezetésre: az entrópia. A termodinamika második alaptörvénye az entrópia felhasználásával a következőképpen fogalmazható meg: a spontán folyamatok esetében a magukra hagyott rendszerek entrópiája csak növekedhet.
III. főtétel
Nernst megfogalmazása szerint az abszolút tiszta kristályos anyagok entrópiája nulla kelvin hőmérsékleten zérus. Olyan abszolút tiszta kristályos anyag, amelyre a Nernst megfogalmazása érvényes lenne, a természetben nem fordul elő, ideális fogalom, tehát nulla entrópiájú anyag nem létezhet. Az entrópia határértékét a harmadik főtétel pontosított megfogalmazása a következőképpen rögzíti: a termodinamikai rendszerek entrópiája véges pozitív érték felé, az entrópia hőmérséklet szerinti deriváltja pedig a zéró felé tart, amikor a rendszer hőmérséklete az abszolút nulla érték felé közelít. Nernst posztulátumát később egy újabb megfogalmazásban hozta nyilvánosságra, mely szerint az abszolút nulla hőmérséklet tetszőlegesen megközelíthető, de nem érhető el. E kijelentés a harmadik főtétel előbbi megfogalmazásának következménye: mivel az abszolút nullához közeli hőmérsékleten az anyagok fajhője nagyon kicsi, igen kis hőmennyiség a hőmérséklet jelentős megváltozásához vezet. Bármilyen módon is valósítjuk meg a hűtést, a lehűtendő test valamilyen fokú visszamelegedése elkerülhetetlen. A folyamat megismétlésével a hőmérséklet tovább csökkenthető, tehát végső soron az abszolút nulla hőmérséklet elvileg tetszőleges pontossággal aszimptotikusan megközelíthető, de nem érhető el.
Termodinamikai potenciálok
Bizonyos termodinamikai paramétereket elterjedten neveznek termodinamikai potenciál-függvényeknek is. Ez annyit jelent, hogy - hasonlóan a mechanikában és az elektrodinamikában értelmezett potenciál-függvényekhez - skálázásuk egy állandó erejéig önkényesen végezhető el, azonban a választott skálától függetlenül szélsőértékük helye egyértelműen kijelöli a vizsgált rendszer egyensúlyi állapotát.
Ötféle termodinamikai potenciált különböztetünk meg[4]:
| Név | Jelölés | Képlet | Természetes változók |
|---|---|---|---|
| Belső energia | 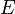
|
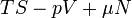
|
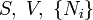
|
| Helmholtz szabadenergia | 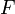
|
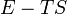
|
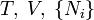
|
| Entalpia | 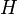
|
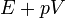
|
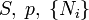
|
| Gibbs szabadentalpia | 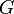
|
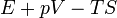
|
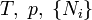
|
| Landau potenciál | 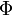
|
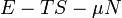
|
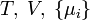
|
A fundamentális egyenlet
Fundamentális egyenletnek azt nevezzük, ami három extenzív változótól függ, pl: S(N, E, V). Fundamentális egyenletből a makroszkopikus rendszerre vonatkozó információk mind kinyerhetőek (ha ezt tudjuk, a rendszer egész termodinamikáját ismerjük).
A fundamentális egyenlet (S(E, V, N)) differenciális alakja:
Megfelelően alkalmazva Legendre-transzformációkat a többi potenciál differenciális alakja:
Van der Waals gázok
A létező (reális) gázok tulajdonságai többé-kevésbé eltérnek az ideális gázok tulajdonságaitól. Az eltérés oka abból adódik egyrészt, hogy a gázatomok, -molekulák kölcsönösen vonzzák egymást – ún. van der Waals-erők működnek közöttük –, másrészt nem pontszerűek, van kiterjedésük, azaz saját térfogattal rendelkeznek.
Ha az ideális gáz egyenletébe beírjuk a nyomás- és térfogati korrekciókat, akkor n anyagmennyiség esetén a:
kifejezést kapjuk, amely a reális gázokra vonatkozó van der Waals-egyenlet.
Ha az összefüggésből kifejezzük a nyomást, az alábbi, viszonylag bonyolult összefüggéshez jutunk:
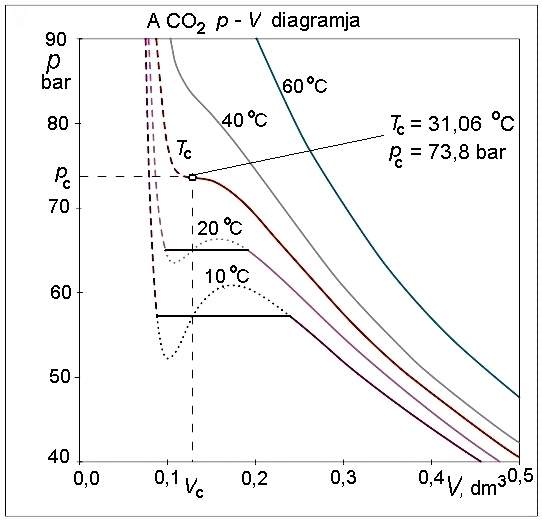
Elvégezve a kijelölt műveleteket és rendezve az egyenletet, a
kifejezésből látható, hogy a térfogatra nézve a függvény harmadfokú, mint a mellékelt ábra – a szén-dioxid p–V diagramjának – izotermáin is látható.
Reális gázokkal végezhető kísérletek pl. Gay-Lussac, Joule-Thomson
Fázisátalakulások
- a régi verzióban: Fázisátalakulások termodinamikai tárgyalása és Fázisegyensúlyok
Jellemzői
A termodinamika által leírt folyamatok közül kiemelkedő fontosságúak azok, ahol a folyamat kezdeti anyaga és a folyamat végén keletkezett anyag lényegesen különböző tulajdonságokkal rendelkezik.[5]
A fázisátalakulásokat gyakran kíséri a túlhűtés, ritkábban a túlhevítés jelensége. Előbbit használja ki a Wilson-féle ködkamra, utóbbit a buborékkamra.
Típusai
Elsőrendű fázisátalakulás
Elsőrendű fázisátalakulásnak olyan folyamatot hívunk, amikor az intenzív paraméter folytonos változása mellet az extenzív paraméternek ugrása van. A fázisátalakuás kifejezésen rendszerint elsőrendű fázisátalakulást értünk.
Másodrendű fázisátalakulás
Másodrendű fázisátalakulás az elsőrendűtől abban különbözik, hogy itt az extenzív paraméter is folytonos, csak a deriváltjában van rendkívüli viselkedés. Ilyenek például a kritikus opaleszcencia, ferromágneses átalakulás a Curie-hőmérsékleten, ferroelektromos katasztrófa, szupravezetés, szuperfolyékonyság, stb.
Gibbs-féle fázisszabály
Egy termodinamikai rendszer egyensúlyi állapotában egyszerre jelen levő fázisok (fizikailag homogén részek) száma (F), a szabadon választható állapothatározók (vagy szabadsági fokok) száma (Sz) és a rendszert alkotó független komponensek száma (K) közötti összefüggés:
A fázistörvény a termodinamika főtételeiből vezethető le. Pl. ha a víz (egykomponensű rendszer, K = 1) csak egy fázisban (pl. gőzként) van jelen (F = 1), akkor nyomása és hőmérséklete (bizonyos határokon belül) tetszőlegesen változtatható (Sz = 2); míg három különböző fázisban (gőz, folyékony víz és jég, F = 3) már csak egyetlen, meghatározott nyomás- és hőmérsékletértéknél (hármaspont) lehet (Sz = 0).
Fázisdiagramok
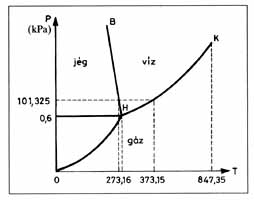
Az olyan diagramot, amit fázisok szerinti tartományokra osztunk fel, fázisdiagramnak nevezzük. A tengelyeken legtöbbször két választott változó, pl. p-T felmérése mellett, ilyenkor a többi változót rögzítjük. Szemléletesen: a teljes teret egy síkkal metsszük el. Az ábrákon a víz nyomás-hőmérséklet fázisdiagramja és a titán nikkel ötvözetek hőmérséklet-koncentráció diagramja látható.
A folyadék és légnemű fázisok közötti minőségi különbség megszűnik a kritikus pontnál (K). A kritikus pont felett a folyadékból folytonosan lesz légnemű anyag. Folyadékállapotból légneműbe fázisátalakulás nélkül is eljuthatunk a kritikus pont megkerülésével.
Kémiai potenciál
A kémai potenciál más néven parciális szabadentalpia, parciális Gibbs-energia a rendszer alkotóira jellemző mennyiség.
A kémiai potenciált definiáló összefüggés:
![\mu_\mathrm{i}=\left( \frac{\partial G}{\partial {N_\mathrm i}}\right)_{p,T,N_\mathrm{j\ne i}},\ \left[\mathrm {J}\right]](/images/math/f/9/c/f9c49abcc2cf03bfd427d4ea8e42208e.png) ,
,- ahol
- G a rendszer Gibbs-energiája, [J]
- Ni az i komponenst alkotó atomok száma, [1]
- p a nyomás, [Pa]
- T a hőmérséklet, [K].
Az i komponens kémiai potenciálja egy intenzív fizikai mennyiség, ami megadja, hogy az i komponens változása esetén mennyivel változtatja meg a rendszer szabadentalpiáját, azaz az integrális mennyiségét (miközben a rendszerben a hőmérséklet, a nyomás és az i komponens kivételével az összes többi komponens mennyisége állandó marad). A kémiai potenciál abszolút értéke nem ismeretes, gyakorlatban a folyamatokban bekövetkező megváltozása fontos.
Fázisegyensúlyok
Clausius-Clapeyron egyenlet
A Clausius Clapeyron egyenlet írja le kétfázisú rendszerek egyensúlyának feltételét. A szabadentalpia:
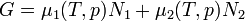
A részecskeszám megmaradás miatt 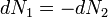 , akkor az egyensúly dG=0 feltételéből visszakapjuk a korábban is említett
, akkor az egyensúly dG=0 feltételéből visszakapjuk a korábban is említett 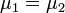 feltételt. Ebből az egy mólnyi mennyiségre vonatkozó
feltételt. Ebből az egy mólnyi mennyiségre vonatkozó 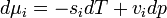 Gibbs-Duhem reláció adja a Clausius-Clapeyron egyenletet:
Gibbs-Duhem reláció adja a Clausius-Clapeyron egyenletet:
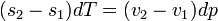
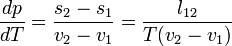
ahol v moláris térfogat, s moláris entrópia, 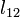 moláris látens hő.
moláris látens hő.
Jegyzetek, hivatkozások
- ↑ Donald L. Turcotte, Gerald Schubert: Geodynamics, 2nd Edition, Cambridge, 2002, ISBN 0-521-66624-4
- ↑ A H jelölés az angol „hot”, azaz „forró”, „meleg” szót rövidíti
- ↑ A C jelölés az angol „cold”, azaz „hideg” szót rövidíti
- ↑ Alberty (2001) p1353
- ↑ Tichy Géza, Kojnok József: Hőtan, Typotex Kiadó, 2001, 75. old., ISBN 963-9326-14-3
- ↑ J. W. Gibbs, 1878