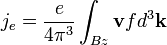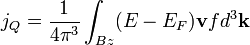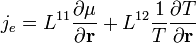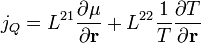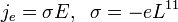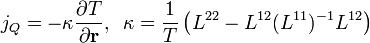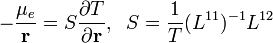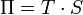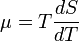Nemegyensúlyi folyamatok leírása
Tartalomjegyzék
Irreverzibilis folyamatok
Az irreverzibilis folyamatokban fontos szerepet játszanak az intenzív fizikai mennyiségekkel (hőmérséklet, nyomás, elektromos potenciál) kapcsolatos hajtóerők. Ezek megfigyelésével vizsgálhatjuk a nyílt rendszerek időfüggő energetikai folyamatait, illetve választ adhatunk arra is, hogy egy folyamat miért gyors vagy lassú.
Egy tetszőleges termodinamikai rendzser entrópiaváltozása két tagból tevődik össze: egy külső forrásból eredő (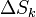 ) és egy belső entrópiaváltozással kapcsolatos (
) és egy belső entrópiaváltozással kapcsolatos (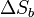 ). A belső entrópia változás nem a környezettel való energiacserével kapcsolatos, hanem a rendszerben lejátszódó termodinamikai folyamatok következménye. Irreverzibilis folyamatban a belső entrópia értéke mindig nő (reverzibilisnél állandó).
). A belső entrópia változás nem a környezettel való energiacserével kapcsolatos, hanem a rendszerben lejátszódó termodinamikai folyamatok következménye. Irreverzibilis folyamatban a belső entrópia értéke mindig nő (reverzibilisnél állandó).
Nyílt rendszerre általában igaz, hogy a belső entrópia nő, de csökkenhet is. Nagyon fontos az irreverzibilis folyamatokban az idő, jellemzően a mennyiségek időderiváltjai fizikai jelentést hordoznak.
Entrópiaprodukciónak nevezzük a belső entrópia időbeli változásának gyorsaságát, vagyis:
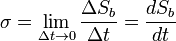 .
.
Az időegység alatti belsőentrópia-változás mértékegysége 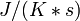 .
.
Az entrópia megváltozásának teljes egyenlete:
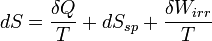 , ahol
, ahol
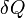 a hőváltozás,
a hőváltozás, 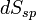 a spontán entrópiaváltozás (mindig nagyobb 0-nál),
a spontán entrópiaváltozás (mindig nagyobb 0-nál), 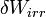 az irreverzibilis folyamat alatt végett munka, T a hőmérséklet.
az irreverzibilis folyamat alatt végett munka, T a hőmérséklet.
- Pl.: Ha veszünk egy zárt rendszert (két kamra: egyikben gáz, másikban vákuum) és elvesszük a falat, akkor a gáz kitölti a másik térrészt is. Ekkor: Q=0, W=0,
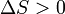 !!
!!
- A lényeg, hogy a rendszer önmagával legyen egyensúlyban. A fenti egy spontán irreverzibilis folyamat (kvázisztatikus rendszer folyamat). Egy ilyen során az entrópia keletkezik. Tehát az entrópia nem marad meg, de csak keletkezni “szeret”.
További példás spontán S termelődésre (ha zárt rsz. nincs egyensúlyban, akkor S nőni fog):
Pl. Gay-Lussac-kísérlet: vákuummal szembeni tágulás: 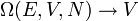 nő
nő 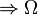 nő
nő 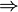 S nő....
S nő....
Pl2. Eltérő hőmérsékletű tartályok: 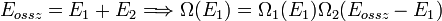 ekkor
ekkor 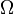 eléri a max értéket és S spontán nőni fog...
eléri a max értéket és S spontán nőni fog...
Master egyenlet, részletes egyensúly.
megjegyzés: a jobb olvashatóság érdekében az ábrán szereplő: n'=m
Van egy rendszerünk, aminek van n diszkrét állapota, amik között ugrál.
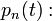 - annak a valószínűsége, hogy a rendszer az n-edik állapotban van.
- annak a valószínűsége, hogy a rendszer az n-edik állapotban van.
- Tegyük fel, hogy tudom, hogy egységnyi idő alatt mi annak a valószínűsége, hogy a rendszer n-ből m állapotba megy át.
Ennek jelölése: 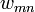 . Nem tudunk róla semmit, de tegyük fel, hogy ismerjük az értékét.
. Nem tudunk róla semmit, de tegyük fel, hogy ismerjük az értékét.
- Tegyük fel, hogy az átmenetek folyamata Markov-folyamat, tehát létezik olyan
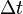 , hogy már csak a t mondja meg, hogy mi történik
, hogy már csak a t mondja meg, hogy mi történik 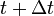 -ben. (És tegyük fel, hogy az átmenetek megvalósulnak.)
-ben. (És tegyük fel, hogy az átmenetek megvalósulnak.)
Ekkor:
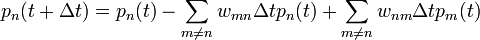
Azt szeretnénk megtudni, mekkora valószínűséggel lesz a rendszerünk az n. állapotban 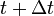 időpillanatban. Ez szerepel az egyenlet bal oldalán.
időpillanatban. Ez szerepel az egyenlet bal oldalán.
A jobboldalon a következő tagok állank:
- 1. tag: Annak valószínűsége, hogy már t időpillanatban is az n. állapontban volt a rendszer (ezt ismertnek tekintjük)
- 2. tag: Annak valószínűsége, hogy t időpillanatban az n. állapotban volt, és
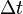 idő múlva ellépett onnan (ezért levonjuk)
idő múlva ellépett onnan (ezért levonjuk)
- 3. tag: Annak valószínűsége, hogy t időpillanatban az másik állapotban volt, de
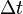 idő múlva az n. állapotba került.
idő múlva az n. állapotba került.
- (
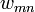 és
és 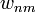 egységnyi időre vonatkozik)
egységnyi időre vonatkozik)
- (
Sorba fejtek 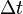 körül, így
körül, így 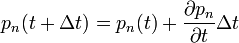
Ezt felhasználva 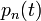 kiesik, majd
kiesik, majd 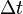 -vel egyszerűsíthetünk. Ami marad::
-vel egyszerűsíthetünk. Ami marad::
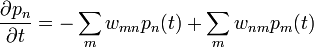
A Master-egyenlet diszkrét állapottérben
Ennek kell, hogy legyen stacionárius megoldása, amihez relaxál: (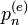 - egyensúlyi valószínűség)
- egyensúlyi valószínűség)
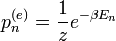 , ahol
, ahol 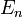 az n-edik állapot energiája.
az n-edik állapot energiája.
Ha ezt helyettesítem be, akkor a bal oldal 0 lesz.
Vizsgáljuk ezt egy egyszerű példán keresztül: bináris atomok rendszere.
Két energiaszint lehetséges: 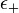 (ilyen atomok száma
(ilyen atomok száma 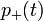 ),
), 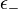 (ilyen atomok száma
(ilyen atomok száma 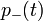 ).
).
Az átmenetek valószínűsége: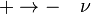 ;
; 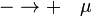 .
.
Írjuk fel egy későbbi időpontban az 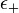 energiájú atomok számát:
energiájú atomok számát: 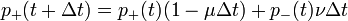 .
.
A jobb oldal első tagja adja meg, hány részecske nem váltott állapotot, míg a második tag azt, mennyi váltott.
Némi átrendezés után 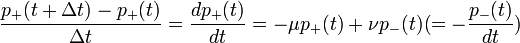 .
Tételezzük továbbá fel, hogy normált az eloszlás:
.
Tételezzük továbbá fel, hogy normált az eloszlás: 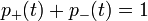 .
A stacionárius megoldás a normáltsági feltétellel a következőre vezet:
.
A stacionárius megoldás a normáltsági feltétellel a következőre vezet: 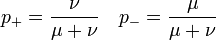 .
.
Beírva a Boltzmann-faktort, a stacionárius megoldás:
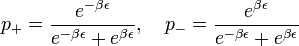 .
A kettő arányára pedig fennáll a következő: Értelmezés sikertelen (Hiányzó <code>texvc</code> végrehajtható fájl; a beállítást lásd a math/README fájlban.): \dfrac{p_{+}}{p_{-}}=e^{-2 \beta \epsilon}=\dfrac{\nu}{\mu} *Tegyük fel, hogy meg tudom úgy adni az átmeneti [[valószínűség]]eket, hogy a rendszer beugorjon az egyensúlyi állapotba. *Hogyan kell megválasztani az átmeneti valószínűségeket? '''Az átmeneti valószínűségek megválasztása''' * Egyensúlyban [[időtükrözési szimmetria]] van. [[Kép:egyensuly.png|center|thumb|A rendszer két állapota közötti átmeneti valószínűségek "kimérése"]] Számolom, hogy (irány szerint megkülönböztetve) hányszor megy egyikből a másik állapotba a rendszer. * Stacionárius állapotban <math>\Delta t
idő alatt az átmenetek száma:
.
A kettő arányára pedig fennáll a következő: Értelmezés sikertelen (Hiányzó <code>texvc</code> végrehajtható fájl; a beállítást lásd a math/README fájlban.): \dfrac{p_{+}}{p_{-}}=e^{-2 \beta \epsilon}=\dfrac{\nu}{\mu} *Tegyük fel, hogy meg tudom úgy adni az átmeneti [[valószínűség]]eket, hogy a rendszer beugorjon az egyensúlyi állapotba. *Hogyan kell megválasztani az átmeneti valószínűségeket? '''Az átmeneti valószínűségek megválasztása''' * Egyensúlyban [[időtükrözési szimmetria]] van. [[Kép:egyensuly.png|center|thumb|A rendszer két állapota közötti átmeneti valószínűségek "kimérése"]] Számolom, hogy (irány szerint megkülönböztetve) hányszor megy egyikből a másik állapotba a rendszer. * Stacionárius állapotban <math>\Delta t
idő alatt az átmenetek száma:
- n-ből m-be menve:
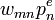
- m-ből n-be menve:
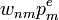
- n-ből m-be menve:
- A részletes egyensúly elve azt mondja ki, hogy a két számnak meg kell egyeznie, azaz:
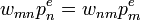
Megkötés az átmeneti valószínűségek hányadosára
Ha az állapotok száma véges és a rendszer minden pontjából minden másik pontjába el tudok jutni, akkor egyetlen stacionárius állapot lesz, az egyensúlyi.
Csak az átmeneti valószínűségek hányadosára van megkötés, azaz:
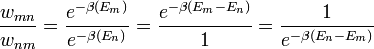
Ha 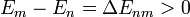 (azaz az energia nő), az e-ados tag 1-nél kisebb lesz, tehát vehetem azt az átmeneti valószínűségnek. Ha csökken az energia, akkor az energiacsökkenés felé vivő lépést 1 valószínűséggel lépem meg.
(azaz az energia nő), az e-ados tag 1-nél kisebb lesz, tehát vehetem azt az átmeneti valószínűségnek. Ha csökken az energia, akkor az energiacsökkenés felé vivő lépést 1 valószínűséggel lépem meg.
Bizonyítás: 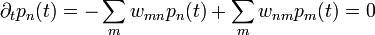 (egyensúly esetén). Tehát:
(egyensúly esetén). Tehát:
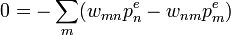 Páronként kioltják egymást. Ezért hívják részletes egyensúlynak, mivel nem csak az egész összeg nulla, hanem az állapotok között páronként van egyensúly. (Ehhez egy összefüggő gráf kell)
Páronként kioltják egymást. Ezért hívják részletes egyensúlynak, mivel nem csak az egész összeg nulla, hanem az állapotok között páronként van egyensúly. (Ehhez egy összefüggő gráf kell)
Entrópia és szabadenergia
Ide még jön egy szemléletesebb magyarázat az entrópiára (pl másik tételben is szerepel.) Cz
Tulajdonképpen valószínűleg ide a Bércesék által írt Mechanika II.-ből a 550-552 oldal környéke a legrelevánsabb. 94.27.225.23 2009. június 22., 09:14 (UTC)
Irreverzibilis folyamatok
Ha egy rendszert például master egyenelttel írunk le, abból is levezethető az entrópia és a szabadenergia. Az entrópia triviálisan felírható az állapotok valószínűségeiből:
Ebből pedig a szabadenergia:
Az irreverzibilis szabadenergia mindig nagyobb, mint a reverzibilis folyamatokban. Az entrópiára pedig továbbra is a második főtétel alkalmazható.
Ismétlésül: A termodinamikai entrópia fogalma:, ahol Q a hő (azaz két különböző hőmérsékletű rendszer közötti spontán energiacsere), dS pedig az entrópiaváltozás. Átrendezve:
Állapotjelzők: extenzív (összeadódik): n, belső energia, V, S intenzív (kiegyenlítődik): p, T,
A Termodinamika első főtétele:
(egy komponensű elegyre) A Termodinamika második főtétele:
Fundamentális egyenlet az előző kettőből:
Termodinamikai Potenciálok: Alapvető skalár potenciálok, természetes változóikban állandó rendszer esetén minimumra törekszenek, azaz egyensúlyban minimálisak. U, F, H, G négy termodinamikai potenciál: * A szabad energia definíciója: F = U - TS * Az entalpia definíciója: H = U + pV * A szabad entalpia definíciója: G = U + pV – TS = H - TS A belső energiára vonatkozó fundamentális egyenletből Legendre transzformációval további Fundamentális egyenletek kaphatóak. Pl:
A Boltzmann-féle entrópia definíciója:
ahol
a mikroállapotok száma. Kanonikus tárgyalásmódban az állapotösszeg:
Ezt, az első fundamentális egyenletet és a Boltzmann-entrópi definícióját felhasználva:
További sűrűn használatos, származtatható összeföggések:
Fundamentális egyenletekből:
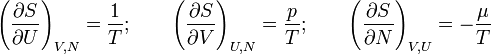
Ezekből felírható a Helmholtz-egyenlet:
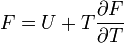
Ingadozási jelenségek
Brown-mozgás, Diffúzió, Brown-mozgás potenciálban
Alapfeltevések
- A részecskék egymástól függetlenül mozognak.
-
 << megfigyelési idő minimuma (ezen túl a mozgás az előzőektől függetlennek tekinthető)
<< megfigyelési idő minimuma (ezen túl a mozgás az előzőektől függetlennek tekinthető) - Az elmozdulásnak van egy valószínűségi eloszlása. A mozgás leírható valószínűségi alapon.
Jelölések
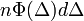 : annak valószínűségét adja meg, hogy n darab részecske
: annak valószínűségét adja meg, hogy n darab részecske 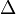 -t ugrik
-t ugrik  idő alatt.
idő alatt.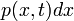 : annak valószínűsége, hogy t időpontban alatt x-ben van a részecske.
: annak valószínűsége, hogy t időpontban alatt x-ben van a részecske.
Az Einstein-féle leírás (1905)
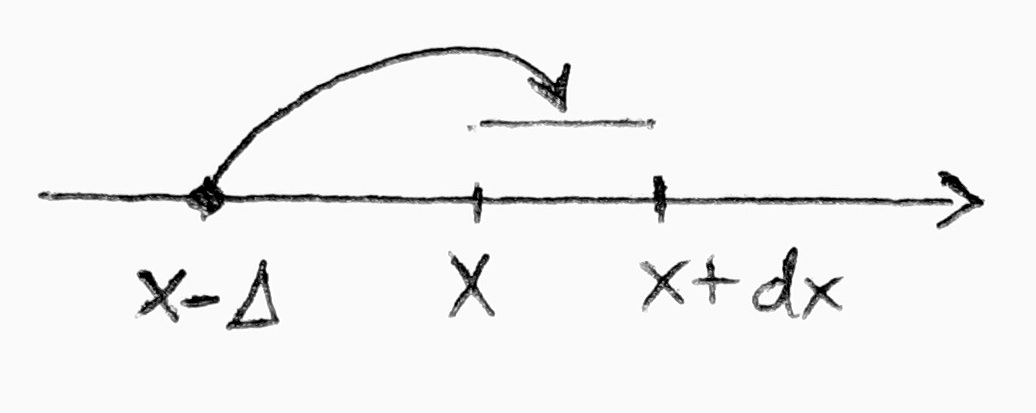
- Annak valószínűsége, hogy a részecske
 idő múlva az x és x+dx közötti tartományban foglal helyet:
idő múlva az x és x+dx közötti tartományban foglal helyet: 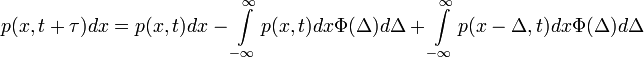
- Az egyenlet jobb oldalának első tagja annak valószínűsége, hogy a részecske már t időpillanatban is az x és x+dx közötti tartományban volt. A második tag annak valószínűségét adja meg, hogy
 idő múlva éppen arrébbmegy egy bármekkora
idő múlva éppen arrébbmegy egy bármekkora 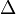 ugrással másik helyre. A harmadik tag annak valószínűségét adja, hogy a részecske valamekkora
ugrással másik helyre. A harmadik tag annak valószínűségét adja, hogy a részecske valamekkora 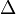 távolságról éppen
távolságról éppen 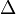 -t ugorva megérkezik
-t ugorva megérkezik  idő múlva.
idő múlva.
- Az egyenletet dx-szel végigoszthatjuk hiszen a dx-ek (és a p(x,t) is) mindegyik integráljel elé kiemelhetőek, hiszen nem függnek
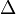 -tól, ekkor:
-tól, ekkor:
- És mivel
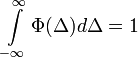 (hiszen
(hiszen 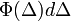 annak valószínűségét adja meg, hogy egy részecske
annak valószínűségét adja meg, hogy egy részecske 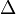 -t ugrik
-t ugrik  idő alatt, aminek a valószínűsége a teljes térre egy kell, hogy legyen - itt jegyzem meg, hogy
idő alatt, aminek a valószínűsége a teljes térre egy kell, hogy legyen - itt jegyzem meg, hogy 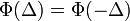 ), ennek következtében a jobb oldal első két tagja kiejti egymást és az egyenlet a következő alakra egyszerűsödik:
), ennek következtében a jobb oldal első két tagja kiejti egymást és az egyenlet a következő alakra egyszerűsödik:
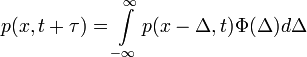
Chapman-Kolmogorov egyenlet
A fenti egyenletet  -ban és
-ban és 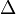 -ban sorbafejtjük, az alábbiak szerint:
-ban sorbafejtjük, az alábbiak szerint:
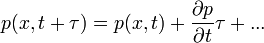
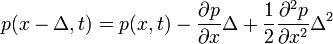
Ekkor a következő egyenletet kapjuk:
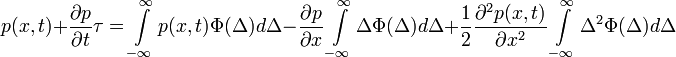
Ugyanazon okok miatt, mint a Chapman-Kolmogorov egyenlet levezetésénél, az egyenlet bal oldalának első tagja és jobb oldalának első tagja kiejti egymást, így a következő marad:
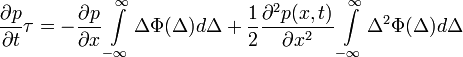
A fenti egyenlet jobb oldalán az első tagnál az integrál pont 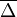 értékét adja meg, míg a második tag integrálját ennek mintájára elneveztük
értékét adja meg, míg a második tag integrálját ennek mintájára elneveztük 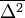 -nek. Az egyenlet a következőképp módosul:
-nek. Az egyenlet a következőképp módosul:
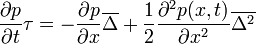
Ám 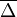 értéke nulla, mivel a
értéke nulla, mivel a 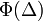 függvényt teljesen szimmetrikusnak tételeztük fel. Tehát a bal oldal első tagja is kiesik. Ami marad:
függvényt teljesen szimmetrikusnak tételeztük fel. Tehát a bal oldal első tagja is kiesik. Ami marad:
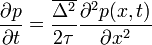
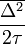 -et D-nek (azaz diffúziós együtthatónak) elnevezve megkapjuk a diffúziós egyenlet általános alakját, mely:
-et D-nek (azaz diffúziós együtthatónak) elnevezve megkapjuk a diffúziós egyenlet általános alakját, mely:
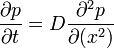
Dinamikai egyenlet a valószínűség időbeni változására (más néven a Fokker-Planck egyenlet).
A Fokker-Planck egyenlet megoldásának keresése
A következőkben a Fokker-Planck egyenlet megoldását kerestük a t = 0, x = 0 kezdőfeltételekhez.
Ekkor ha 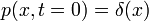 akkor ebből a megoldás:
akkor ebből a megoldás:
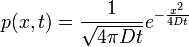 (3D-ben az 1/gyök-ös rész a 3/2-en van.)
(3D-ben az 1/gyök-ös rész a 3/2-en van.)
A fentiek alapján 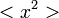 értékére az alábbi összefüggés születik, ahol
értékére az alábbi összefüggés születik, ahol 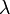 -t konstansnak várjuk:
-t konstansnak várjuk:
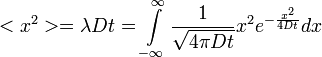 =
=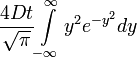
az utolsó egyelőségnél változó helyettesítés történt: 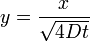
Az integrál értéke innen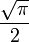 így:
így:
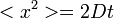 (azaz
(azaz 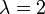 )
)
Sodródás, Brown-mozgás potenciálban:
A részecskék ebben az esetben valamilyen kitüntetett irányba sodródnak: 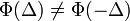
Az előzőekhez képest annyi a különbség, hogy a következő tag:
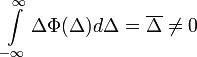
Ismét alkalmazva a Kramers-Moyal sorfejtést:
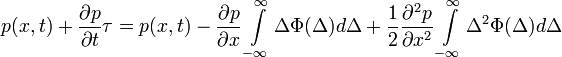
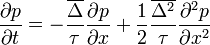
(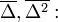 mikroszkopikus hossz,
mikroszkopikus hossz, 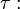 mikroszkopikus idő.)
mikroszkopikus idő.)
Ez is a Fokker-Planck egyenlet egy alakja. A fenti egyenlet jobb oldalán az első tag önmagában egy driftet ír le:
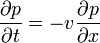 , ahol
, ahol 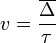
Például: 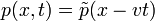 . A fenti egyenletbe behelyettesítve és elvégezve:
. A fenti egyenletbe behelyettesítve és elvégezve: 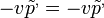
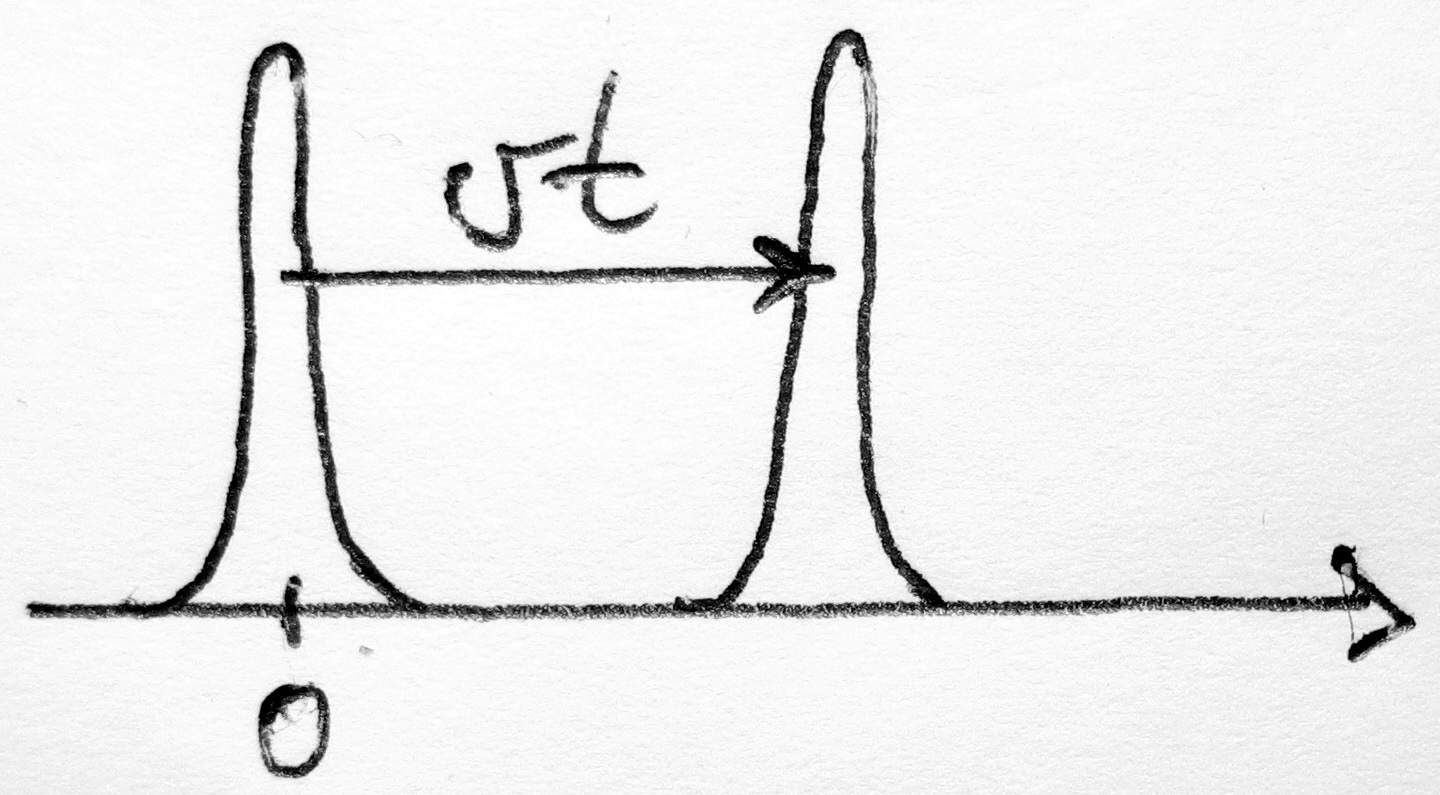
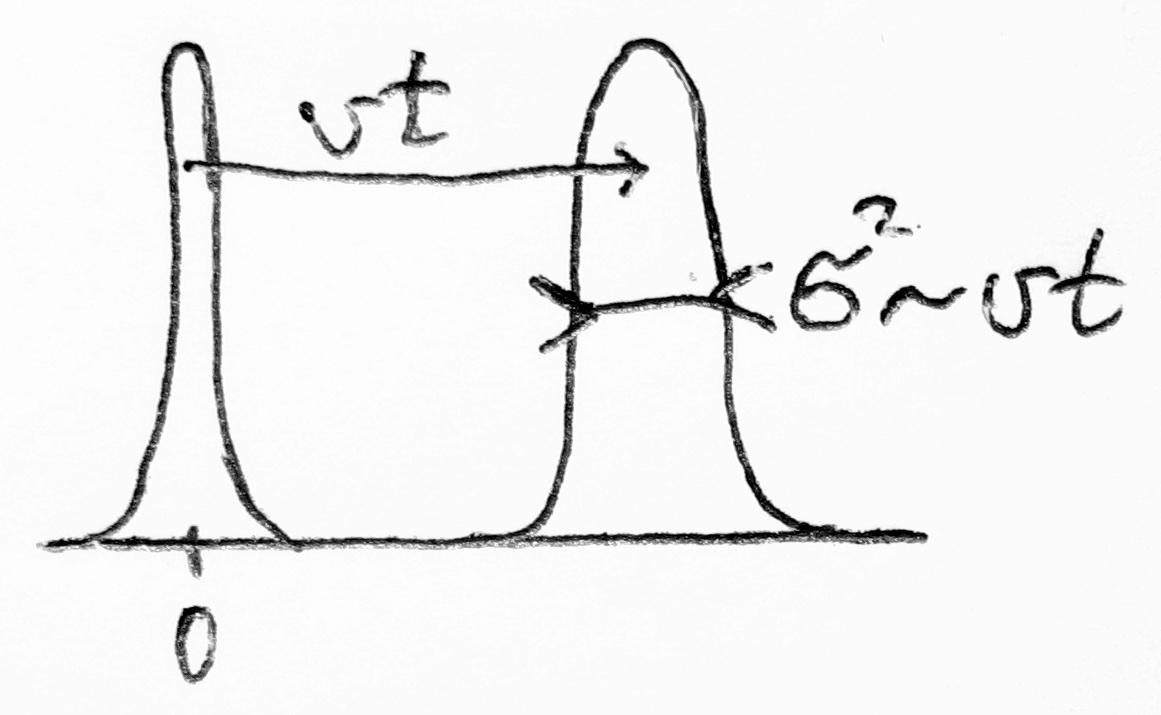
Viszont érdemes megtartani a második tagot, hiszen ha ezt is figyelembe vesszük, akkor azt kapjuk, hogy a "csomag" halad valamerre és közben szétterjed:
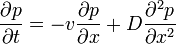
Bevezetve az y := x-vt -t (vagyis "beleülünk" a driftelő rendszerbe), akkor 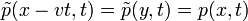 . Ekkor a Fokker-Planck egyenlet a következőképp múdosul:
. Ekkor a Fokker-Planck egyenlet a következőképp múdosul:
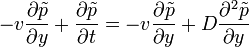 Vagyis visszakapjuk a drift nélküli összefüggést:
Vagyis visszakapjuk a drift nélküli összefüggést: 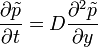
Tehát: 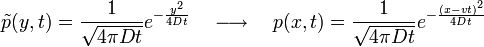
Langevin-egyenlet
Brown-mozgásra az általános Langevin-egyenlet: 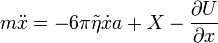 , ahol
, ahol
-
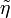 - a viszkozitás
- a viszkozitás
- a - a részecske sugara
- X - egy véletlenszerű erő
-
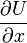 - egy külső erő (potenciál)
- egy külső erő (potenciál)
Ha túlcsillapított esetet vizsgálunk, akkor 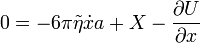
Ekkor bevezetve a zajt - 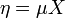 - fogalmát és a
- fogalmát és a 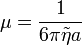 jelölést, az egyenlet a következőképp fog kinézni:
jelölést, az egyenlet a következőképp fog kinézni:
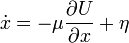
Bevezetve még a 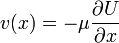 jelölést:
jelölést:
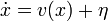 lesz a végleges forma.
lesz a végleges forma.
Ebből jól látni, hogy túlcsillapított esetben az elmozdulás a 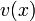 determinisztikus sebesség és az
determinisztikus sebesség és az 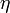 zaj összege.
zaj összege.
Ha feltételezzük, hogy a zaj Gauss-eloszlású, és meghatározzuk az adott helyen tartózkodás valószínűségét, akkor megkapjuk a “driftet tartalmazó” Fokker-Planck egyenletet (lsd. feljebb)
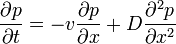
Bevezetve a valószínűségi áramot: 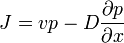 , egyensúlyi esetben (J=0) megkapjuk a Boltzmann-eloszlást:
, egyensúlyi esetben (J=0) megkapjuk a Boltzmann-eloszlást:
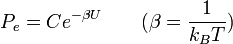
Vezetési jelenségek
Drude modell
Az elektromos vezetés jelenségét úgy tekintjük, hogy az elektronok az elektromos tér hatására gyorsulnak, azonban a vezető helyezkötött atomtörzseinek ütközve energiát veszítenek. Ez igen hamar makroszkópikus egyensúlyhoz vezet, ha a tér nem változik. Ezek a feltevések az alapjai a Drude-modellnek, amelynek eredménye az elektronokra felírható mozgásegyenlet:
amelynek stacionárius megoldása:
Itt  az ütközések között eltellő jellemző relaxációs idő, v a drift sebesség. A v-re rendezett eredményt a töltéssel (e) és az elektronsűrűséggel (n) beszorozva megkaphatjuk az Ohm-törvényt:
az ütközések között eltellő jellemző relaxációs idő, v a drift sebesség. A v-re rendezett eredményt a töltéssel (e) és az elektronsűrűséggel (n) beszorozva megkaphatjuk az Ohm-törvényt:
azaz az elektromros áramsűrűség egyenesen arányos a térerősséggel, az arányossági tényező a fajlagos ellenállás reciproka, azaz a fajlagos vezetőképesség. A Drude-moell jó leírást ad több effektusra, azonban például az áram hőhatását túlbecsli. Kevés jó modell van az elektronok ütközésének leírására, ez a terület ma is aktív kutatás tárgya.
Kereszteffektusok
(* A levezetés csak a kitekintés kedvéért szerepel)
A kereszteffektusok bevezetéséhez a nemegyensúlyi statisztikus fizika eszköztárához kell fordulnunk. Ebben a tárgyalásban most a vezetési jelenségekre korlátozódva jellemezze a vizsgált rendszerünket az f betöltési függvény, amely a pozíció, idő, és a hullámvektor függvénye. Írjuk fel a teljes idő differenciát, amely a Liouville-tétel értelmében zérus:
itt X az ütközések miatti változást jelöli. A felírt egyenlet lényegébena Boltzmann-egyenlet, csak impulzus helyett hullámszámra felírva. A következő feltevéseket tehetjük:
- Egyensúlyban a betöltést a Fermi-Dirac statisztika írja le:
vigyázat, 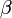 -ban T függhet a helytől is.
-ban T függhet a helytől is.
- A perturbációk időfüggését elhanyagoljuk, azaz f időderiváltja zérus.
- A rendszerben hullámcsomagokat akarunk leírni. Jó leírást kapunk, ha a sebességre a csoportsebességet vezetjük be:
- Az impulzusmegváltozással analóg tagra írjuk be a klasszikus elektromágneses erőhatást:
- Az ütközési tagra tegyük azt a durva közelítést, hogy az egyensúlytól való eltéréssel egyenesen, és a relaxációs idővel fordítottan arányos:
- Az eloszlásfüggvény helyszerinti gradiense a hőmérséklet függésen keresztül is kifejezhető:
A fentiek ismeretében a Boltzmann-egyenlet a következő alakra kerül:
A deriválásokat egy D differenciál-operátorba összevonva az egyenlet:
Ennek a megoldása felírható soralakban, így különböző rendű korrekciók nyerhetőek:
Ezt visszahelyettesítve elsőrendben a következő megoldást kapjuk:
A legszembetűnőbb eredmény, hogy a mágneses tér kiesett, azaz csak a magasabb rendű korrekciók függnek tőle. Ha bevezetjük az elektromos áramsűrűséget, és a hőáramsűrűséget:
és bevezetve egy egyesített potenciált: 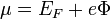 , megkaphatjuk az áramokra vonatkozó egyenleteket:
, megkaphatjuk az áramokra vonatkozó egyenleteket:
Az L együtthatók másodrendű tenzorok, itt most annyi elég róluk, hogy:
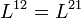 , ez az Onsager-reláció a termodinamikában,
, ez az Onsager-reláció a termodinamikában,- Mindegyikük tartalmazza az egyensúlyi eloszlás energia szerinti deriváltját, és
 -t,
-t, - Az
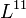 tenzor ezen felül az elektromos töltést,
tenzor ezen felül az elektromos töltést, 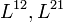 tartalmazza
tartalmazza 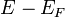 -et,
-et,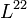 pedig
pedig 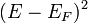 -et.
-et.
Ezek segítségével kifejezhetőek a következők:
- Homogén anyagban, homogén hőmérsékleteloszlás esetén visszakapjuk az Ohm-törvényt:
- Homogén anyagban, ha nincs elektromos áram visszakapjuk a hővezetés egyenletét:
és az elektrokémiai potenciál, valamint a hőmérsékletgradiens kapcsolatát:
Ezek kombinálásával lehet értelmezni a további effektusokat (ekkor már elhagyható a fenti megkötések egy része):
- Seebeck-effektus: a hőmérsékletkülönbség elektromos áramot hoz létre.
- Peltier-effektus: két fém határfelületén átfolyó áram hőmérsékletkülönbséget hoz létre a két fémen.
- Thomson-effektus: áram alatt levő vezető, amelyen hőmérsékletkülönbség van, lehűl, vagy felmelegszik.
Ezen effektusok arányossági tényezői között fennáll a következő két Thomson-összefüggés:
ahol T a hőmérséklet, 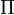 a Peltier-együttható, S a Seebeck-együttható és
a Peltier-együttható, S a Seebeck-együttható és 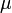 a Thomson-együttható.
a Thomson-együttható.
Az eloszlásfüggvény további korrekcióinak figyelembevételével megkaphatjuk a másodrendű effektusokat, akkor már a mágneses hatás is beleszól a folyamatokba. Ezek közül a legjelentősebb a Hall-effektus. Itt elektromos áram, és rá merőleges mágneses tér hatására az előző kettőre merőleges elektromos potenciálkülönbség alakul ki a vezetőben.
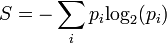
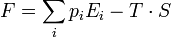
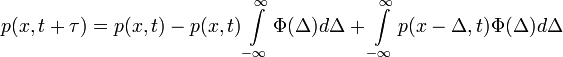
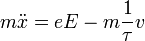
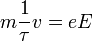
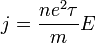
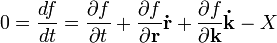
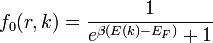
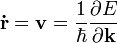
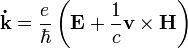
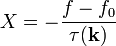
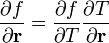
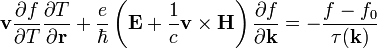
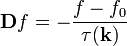
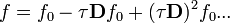
![f = f_0 + \frac{\partial f_0}{\partial E} \tau \mathbf{v} \left[ \left( \frac{E - E_F}{T} + \frac{\partial E_F}{\partial T} \right) \frac{\partial T}{\partial \mathbf{r}} - eE \right]](/images/math/e/b/0/eb0fc5b512db00d7b9bfc83aa515b9bb.png)