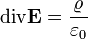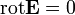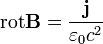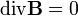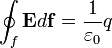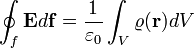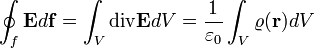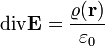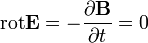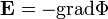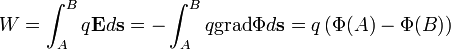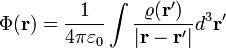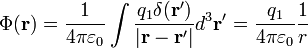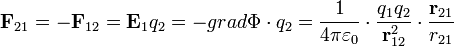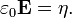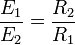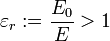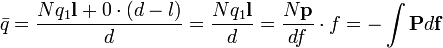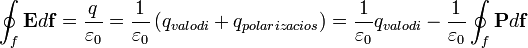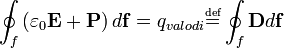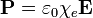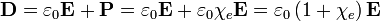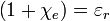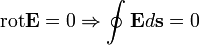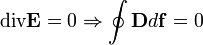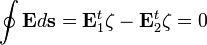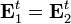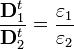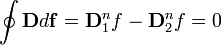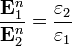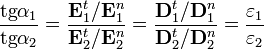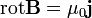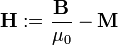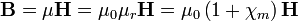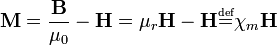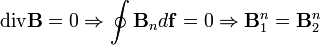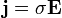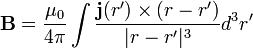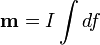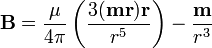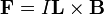Elektro- és magnetosztatika, áramkörök
Tartalomjegyzék
Coulomb- és Gauss-törvény, szuperpozíció elve, stacionárius áram
ELektrosztatika
Sztatika esetén nincsen időbeli változás, tehát a Maxwell-egyenletekben [1] szereplő, időderiváltakat tartalmazó targok 0-t adnak járulákul. Így a sztatikus Maxwell-egyenletek SI-ben:
ahol 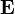 az elektromos térerősség,
az elektromos térerősség, 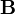 a mágneses indukció,
a mágneses indukció, 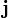 az áramsűrűség,
az áramsűrűség, 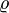 az elektromos töltéssűrűség,
az elektromos töltéssűrűség, 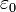 a vákuum dielektromos állandója.
a vákuum dielektromos állandója.
Gauss-törvény
Gauss-törvénynek az első Maxwell-egyenletet nevezzük. Az elektromos töltések, vagy töltéseloszlás, és az elektromos tér kapcsolatát adja meg. Integrális formában azt mondja ki, hogy ha egy 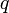 töltést körbeveszünk egy zárt felülettel, akkor arra integrálva az elektromos teret (
töltést körbeveszünk egy zárt felülettel, akkor arra integrálva az elektromos teret (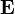 ), a töltéssel arányos mennyiséget kapunk:
), a töltéssel arányos mennyiséget kapunk:
Ahol 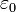 , az arányossági tényező reciproka, a vákuum dielektromos állandója. Általánosabban felírhatjuk töltéseloszlásra is, aminek alesete több ponttöltés:
, az arányossági tényező reciproka, a vákuum dielektromos állandója. Általánosabban felírhatjuk töltéseloszlásra is, aminek alesete több ponttöltés:
Ezt nevezzük a Gauss-törvény integrális formájának. 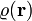 a töltéssűrűség,
a töltéssűrűség, 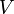 pedig az
pedig az 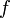 zárt felület által határolt térfogat. A matematikai Gauss-törvény értelmében egy vektortér divergenciájának térfogatra vett integrálja egyenlő a vektortér határfelületre vett integráljával, vagyis:
zárt felület által határolt térfogat. A matematikai Gauss-törvény értelmében egy vektortér divergenciájának térfogatra vett integrálja egyenlő a vektortér határfelületre vett integráljával, vagyis:
Mivel az egyenlet két oldalán ugyanarra a térfogyatra integrálunk, az integrandusok is egyenlőek:
Ez a Gauss-törvény differenciális formája.
Coulomb-törvény
Elektrosztatikában minden időderivált eltűnik: 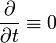 . Így a Faraday-törvény (egy másik Maxwell-egyenlet) így alakul:
. Így a Faraday-törvény (egy másik Maxwell-egyenlet) így alakul:
Rotációmentes vektorterek előállíthatóak egy skalárfüggvény gradienseként, ezért vezessük be a 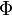 skalárpotenciált, amelyre igaz:
skalárpotenciált, amelyre igaz:
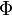 skalárpotenciál dimenziója energia/töltés, így adott töltés esetén arányos a potenciális energiával, és egy
skalárpotenciál dimenziója energia/töltés, így adott töltés esetén arányos a potenciális energiával, és egy 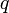 töltést mozgatva elektromos térben
töltést mozgatva elektromos térben 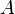 pontból
pontból 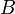 pontba, megadja a végzett
pontba, megadja a végzett 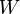 munkát:
munkát:
A gradienses egyenletet beírva a divergenciásba, kapjuk a Poisson-egyenletet:
A levezetést mellőzve, Green-módszerrel megoldható az egyenlet, az általános megoldás pedig:
Ha az Origóban van egyetlen, 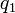 töltésű ponttöltésünk, akkor
töltésű ponttöltésünk, akkor 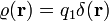 . Erre könnyen el lehet végezni az integrált:
. Erre könnyen el lehet végezni az integrált:
Az ebbe a térbe helyezett 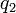 töltésre ható erő:
töltésre ható erő:
Ezt nevezzük Coulomb-törvénynek.
A Maxwell-egyenletek linearitása miatt egy adott pontban különböző töltések által keltett elektromos tér értéke megegyezik az egyéni töltések által létrehozott terek vektoriális összegével. Belátható, hogy ez egyenértékű azzal, hogy az egyes töltések által létrehozott skalárpotenciálok is összeadódnak. Ezt nevezzük a szuperpozíció elvének.
Vezetők, szigetelők, dielektrikumok, kondenzátor, magnetosztatika
Vezetők[2]
Az elektromos vezetők - általában fémek - belsejében a delokalizált elektronok áramlása hozza létre a vezetés jelenségét. Ezt okozhatja például külső elektromos erőtér. Az így létrehozott áramot vagy mozgásban kell tartani egy külső energiaforrással, vagy amint az elektronok kisütik a kezdeti teret létrehozó forrásokat, megállnak. Tehát az elektronok addig mozognak, amíg úgy nem rendeződnek, hogy a belső elektromos tér nulla legyen. Mivel a tér belül zérus, így annak divergenciája is nulla, és a Gauss-törvény értelmében akkor a töltéssűrűségnek is 0-nak kell lennie. Tehát a töltéseknek a vezető felületén kell lenniük. Ez képszerűen is logikus: a töltések taszítják egymást, megpróbálnak elszaladni egymás elől, így előbb-utóbb mindenki a falhoz szorulva figyeli a másikat. Ez egy stabil helyzet, amikor nagyjából maximalizálták az egymás közötti távolságot.
Továbbá a vezető felülete ekvipotenciális felület, a térerősségnek itt merőlegesnek kell lennie mindenhol. Ha lenne érintőleges tag, akkor az elektronok elmozdulnának a felület mentén. A töltéssűrűség arányos a felületnél lévő térerősség nagyságával:
Különböző sugarú vezető gömbök esetében:
Azaz a térerősség fordítottan arányos a sugárral, nagyobb görbületű helyeken kisebb a térerősség, végtelen kis görbület esetén nagy a térerősség. Ezt nevezzük csúcshatásnak. Ez alapján működik a Segner-kerék, vagy a villámhárító, a van de Graaff-generátornál is fontos.
A vezető belsejében a térerősség zérus. Igaz ez a vezető belsejében lévő (üres) üregre is. Ez a Faraday-kalitka.
Dielektrikumok[3]
Először Faraday bácsi fedezte fel, hogy közegekben az elektromos tér lecsökken. A csökkenés szorzófaktorát nevezte 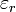 dielektromos állandónak:
dielektromos állandónak:
Ahol 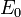 az a térerősség, amit ugyanilyen töltéseloszlás ugyanitt vákuumban hozna létre (pontosabban itt az abszolút értékeket osztjuk egymással). Ennek magyarázata az anyag szerkezetében keresendő. Bizonyos fajta anyagok molekulái rendelkeznek saját
az a térerősség, amit ugyanilyen töltéseloszlás ugyanitt vákuumban hozna létre (pontosabban itt az abszolút értékeket osztjuk egymással). Ennek magyarázata az anyag szerkezetében keresendő. Bizonyos fajta anyagok molekulái rendelkeznek saját 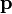 elektromos dipólmomentummal.
elektromos dipólmomentummal.
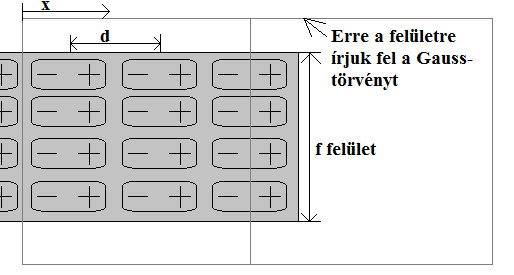
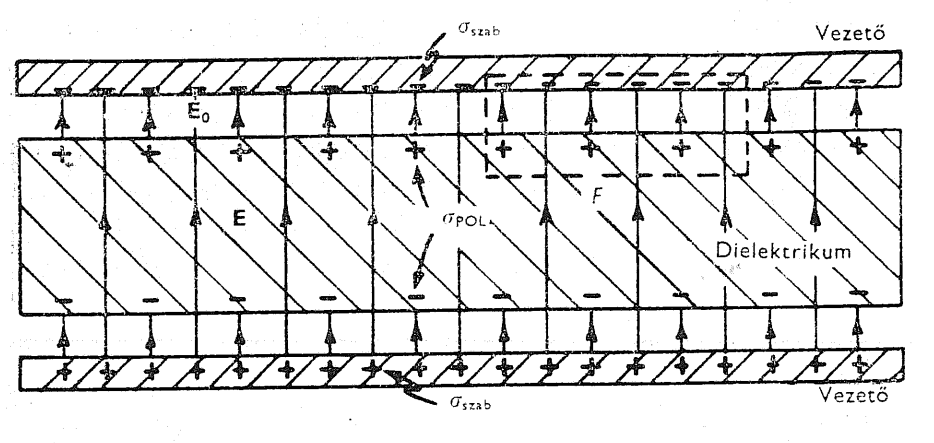
A dipólmomentummal rendelkező molekulákból álló anyagokat nevezzük dielektrikumnak. Elektromos tér hatására ezek a dipólok beállnak a térrel ellentétesen, leárnyékolva (csökkentve) ezzel a teret. Ez látható az alábbi ábrán is, egy egyszerű modellen. Itt a dipólok egy szabályos rácsba helyezve ülnek az anyagban.
Vegyünk egy zárt felületet, amibe belelóg a dielektrikum vége. Erre felírva a Gauss-törvényt az elektromos tér integrálja néhol pozitív lesz (ha éppen kettévágunk egy dipólsort), néhol pedig nulla (ha adott számú semleges dipólt fogtunk körbe). Mivel a dipólok igen kicsik, és közel vannak egymáshoz, ezt egy átlaggal közelíthetjük. Ha az 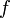 felületen
felületen 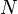 töltés van, és
töltés van, és 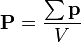 , akkor ez az átlag:
, akkor ez az átlag:
Ez akkor igaz, ha a térfogat, amire integráltunk, tartalmazza a test határfelületét, vagyis van egy effektív, úgynevezett polarizációs töltés a felületen. A Gauss-törvényt módosítva kapjuk:
Ebből:
Ahol 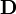 -t nevezzük az elektromos eltolás vektorának.
-t nevezzük az elektromos eltolás vektorának.
Kísérleti tapasztalatok alapján lineáris közeg esetén 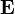 és
és 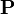 között helyfüggetlen lineáris kapcsolat van:
között helyfüggetlen lineáris kapcsolat van:
Ahol 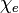 az elektromos szuszceptibilitás. Általános esetben
az elektromos szuszceptibilitás. Általános esetben 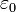 egy szimmetrikus tenzor, de izotrop anyagokban skalár (vagy felfoghatjuk egy konstans és egy egységmátrix szorzatának). Az elektromos eltolás vektor így:
egy szimmetrikus tenzor, de izotrop anyagokban skalár (vagy felfoghatjuk egy konstans és egy egységmátrix szorzatának). Az elektromos eltolás vektor így:
Ekkor definíció szerint:
Ahol 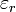 a relatív dielektromos együttható.
a relatív dielektromos együttható. 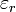 és
és 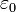 szorzata
szorzata  , a dielektromos együttható (vagy elektromos permittivitás).
, a dielektromos együttható (vagy elektromos permittivitás).
Kondenzátor
Az elektromos töltés tárolására készített technikai eszközöket kondenzátornak (régies nevén „sűrítő”-nek) nevezzük. Minden kondenzátor legalább két párhuzamos vezető anyagból (fegyverzet), és a közöttük lévő szigetelő anyagból (dielektrikum) áll. Az első kondenzátor a leideni palack volt, amelyet Pieter van Musschenbroek készített 1746-ban a leideni egyetemen.
A kondenzátor kapacitása: 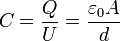 (ahol
(ahol 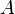 a lemezek területe,
a lemezek területe, 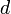 azok távolsága)
azok távolsága)
Kísérleti tapasztalat alapján, ha dielektrikumot teszünk a kondenzátorba, akkor megnő a kapacitás.
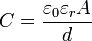 , ahol
, ahol 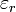 a dielektrikum relatív permittivitása.
a dielektrikum relatív permittivitása.
Mivel a töltések nem változnak, ezért a feszültségnek kell csökkennie. Viszont ez a potenciálkülönbség nem más, mint a fegyverzetek közötti térerősség vonalintegrálja. Ebből az következik, hogy a kondenzátoron belül csökkennie kellett a térerősségnek.
Itt ugyanúgy alkalmazhatjuk a Gauss-tételt, és az ábrán látható (bekeretezett “dielektrikum”) felületre integrálunk, akkor a leutóbbi következtetésünk alapján arra jutunk, hogy kisebb lesz a töltéssűrűség. (Olyan, mintha két kis kondenzátort kötnénk sorba.) Ez csak akkor lehet, ha a szigetelő egyik felén pozitív, másik felén negatív töltés indukálódik. (Vezető esetén tényleg ezt is várnánk...)
Ez okozza a kondenzátor kapacitásának megnövekedését.
Dipólmomentummal nem rendelkező szigetelők molekulái is dipólokká válhatnak külső elektromos tér hatására. Egy elég jól használható magyarázat: az elektronokra és a protonokra más irányú erők hatnak, így torzul a részecske, és az elektronok súlypontja nem esik egybe a protonéval egy részecskén belül. Így kialakul egy dipólus.
Fontos tudni, hogy a polarizáció NEM azonos a megosztás jelenvégével. Ez utóbbiban valódi töltések keletkeznek, és vándorolnak el a vezetőben, ezzel szemben a polarizációban csak atomi méretű töltésszétválás történik!
Számos anyag van, amelyre a fenti lineáris összefüggés nem igaz, a legérdekesebbek talán az elektrétek, amelyek állandó elektromos teret tartanak fenn, hasonlóan az állandó mágnesek mágneses teréhez.
Határfeltételek
Kérdésként merülhet fel, hogy különböző relatív dielektromos állandójú dielektrikumok határán 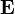 és
és 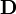 hogyan viselkedik.
hogyan viselkedik.
Az Maxwell-egyenletek integrális alakjából következik, hogy sztatika esetén:
Ezeket kell kielégíteni a határfeltételeken is. Felhasználva, hogy 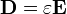 megkaphatjuk a többi komponens transzformációját.
megkaphatjuk a többi komponens transzformációját.
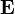 tangenciális komponense folytonosan megy át a határon. Az 1 és 2 közeget elválasztó határfelületen vegyünk fel egy kis (
tangenciális komponense folytonosan megy át a határon. Az 1 és 2 közeget elválasztó határfelületen vegyünk fel egy kis (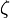 oldalú) négyzetet, a négyzet határfelületre merőleges oldalával tartsunk nullához. Ekkor az első összefüggésből következik, hogy:
oldalú) négyzetet, a négyzet határfelületre merőleges oldalával tartsunk nullához. Ekkor az első összefüggésből következik, hogy:
Azaz két különböző közeg határfelületén az 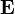 elektromos térerősség érintő irányú komponense folytonosan halad át, a határfelület átlépése során változatlan marad:
elektromos térerősség érintő irányú komponense folytonosan halad át, a határfelület átlépése során változatlan marad:
A 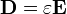 összefüggésből adódik, hogy
összefüggésből adódik, hogy 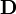 tangenciális komponensének ugrása van a határon:
tangenciális komponensének ugrása van a határon:
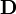 normál komponense folytonosan megy át a határon. Az 1 és 2 közeget elválasztó határfelületen vegyünk fel egy kis (
normál komponense folytonosan megy át a határon. Az 1 és 2 közeget elválasztó határfelületen vegyünk fel egy kis (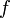 felületű) kockát, a kocka határfelületre merőleges oldalaival tartsunk nullához. Ekkor a második összefüggésből következik, hogy:
felületű) kockát, a kocka határfelületre merőleges oldalaival tartsunk nullához. Ekkor a második összefüggésből következik, hogy:
Tehát az eltolásvektor normál komponense a két közeg határfelületén folytonosan halad át. Viszont a 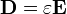 összefüggés alapján az elektromos térerősség normál komponense ugrik:
összefüggés alapján az elektromos térerősség normál komponense ugrik:
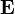 és
és 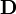 vektorok törési törvénye: Vegyünk fel egy beesési merőlegest a közeg határán és jelöljük az
vektorok törési törvénye: Vegyünk fel egy beesési merőlegest a közeg határán és jelöljük az 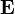 és
és 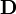 vektorral bezárt szögét
vektorral bezárt szögét 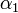 -gyel az egyik közegben (beesési szög) és
-gyel az egyik közegben (beesési szög) és 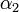 -vel a másik közegben (törési szög), ekkor a következő törvény írható fel:
-vel a másik közegben (törési szög), ekkor a következő törvény írható fel:
Magnetosztatika [1]
A mágneses tér jellemzésre a 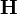 mágneses térerősséget használjuk, a Maxwell-egyenletek alapján sztatika és üres tér estén a következő egyenleteket elégíti ki:
mágneses térerősséget használjuk, a Maxwell-egyenletek alapján sztatika és üres tér estén a következő egyenleteket elégíti ki:
Az divergenciára vonatkozó egyenlet azt írja le, hogy nem létezik mágneses monopólus, szemben az elektromos esettel.
Mágneses tér mágnesezhető anyagok jelenlétében
Hasonlóan mint elektromos tér esetén a polarizáció, itt az közeg mágnesezettsége jelenik meg: 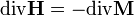 ahol
ahol 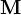 az anyag mágnesezettsége. Ez pici elemi mágneses dipólokból adódik. Ezt adhatják spinek, és köráramok. A mágneses dipól hasonlóan fogható fel, mint egy elektromos, azon kivétellel, hogy nem lehet monopólusokból előállítani, lévén azok elvileg nem léteznek. A elektrosztatikával analóg módón vezessük be a mágneses térerősség vektort:
az anyag mágnesezettsége. Ez pici elemi mágneses dipólokból adódik. Ezt adhatják spinek, és köráramok. A mágneses dipól hasonlóan fogható fel, mint egy elektromos, azon kivétellel, hogy nem lehet monopólusokból előállítani, lévén azok elvileg nem léteznek. A elektrosztatikával analóg módón vezessük be a mágneses térerősség vektort:
Párhuzam állítható az elektrosztatikus, és a magnetosztatikus esetek között: 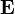 analógja
analógja 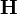 , és
, és 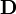 párja
párja 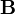 .
.
Lineáris közeg esetén a következő kapcsolat van a mágneses indukció és mágneses térerősség vektor között:
Ahol 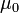 a vákuum mágneses permeabilitása,
a vákuum mágneses permeabilitása, 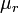 az anyagra jellemző relatív mágneses permeabilitás,
az anyagra jellemző relatív mágneses permeabilitás, 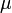 pedig a mágneses permeabilitás.
pedig a mágneses permeabilitás. 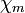 az anyag mágneses szuszceptibilitása. Így a közeg mágnesezettsége és mágneses térerőssége közti kapcsolat:
az anyag mágneses szuszceptibilitása. Így a közeg mágnesezettsége és mágneses térerőssége közti kapcsolat:
Az anyagok két csoportra oszthatóak, attól függően, hogy milyen 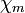 előjele: ha
előjele: ha 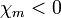 akkor diamágnesről, ha
akkor diamágnesről, ha 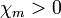 akkor paramágneses anyagról beszélhetünk. Diamágnes lerontja, a paramágnes pedig fölerősíti saját magában a külső mágness teret. Meg kell jegyezni, hogy
akkor paramágneses anyagról beszélhetünk. Diamágnes lerontja, a paramágnes pedig fölerősíti saját magában a külső mágness teret. Meg kell jegyezni, hogy 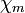 mindkét esetben igen kicsi szám, így a belső és a külső mágneses tér nem sokban különbözik. A szupravezetőkre
mindkét esetben igen kicsi szám, így a belső és a külső mágneses tér nem sokban különbözik. A szupravezetőkre 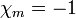 , tehát formálisan hívhatjuk őket tökéletes diamágnesnek, azaz teljesen kiszorítják magukból a mágneses teret, bennük
, tehát formálisan hívhatjuk őket tökéletes diamágnesnek, azaz teljesen kiszorítják magukból a mágneses teret, bennük 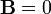 . Azonban a fizikájuk, és
. Azonban a fizikájuk, és 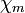 nagyságrendje is gyökeresen eltér a diamágnesekétől, így a kétféle anyagnak nincs sok köze egymáshoz. De ez már egy másik történet... (Vagyis másik tétel.) Diamágneses anyagok szuszceptibilitása hőmérsékletfüggetlen. Paramágneses anyagoknak szuszeptibilitása fordítottan arányos a hőmérséklettel (Courie törvény). Továbbá vannak ferromágneses anyagok, ezeknél
nagyságrendje is gyökeresen eltér a diamágnesekétől, így a kétféle anyagnak nincs sok köze egymáshoz. De ez már egy másik történet... (Vagyis másik tétel.) Diamágneses anyagok szuszceptibilitása hőmérsékletfüggetlen. Paramágneses anyagoknak szuszeptibilitása fordítottan arányos a hőmérséklettel (Courie törvény). Továbbá vannak ferromágneses anyagok, ezeknél 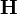 és
és 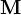 értéke nem arányos, hanem bonyolultabb kapcsolat figyelhető meg.
értéke nem arányos, hanem bonyolultabb kapcsolat figyelhető meg.
Fontos megjegyezni a következő összefüggést:
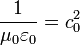
Ahol 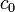 a vákuumbeli fénysebesség. Közegek esetén a fény is lassabban terjed, ekkor sebessége:
a vákuumbeli fénysebesség. Közegek esetén a fény is lassabban terjed, ekkor sebessége: 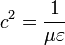 , így látható, hogy a törésmutató ekképp áll elő:
, így látható, hogy a törésmutató ekképp áll elő: 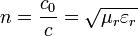 .
.
B és H vektorok viselkedése két közeg határán
Az elektrosztatikában felírtakhoz hasonló alakú határfeltételeket kaphatunk. Mivel a gondolatmenet kb. ugyanaz, csak röviden közlöm:
Stacionárius áram, áramköri törvények: Kirchhoff-törvények, Ohm-törvény
A stacionárius áram kifejezés arra utal, hogy nincsen időbeli változása az áramnak. Ez állandó mágneses teret hoz létre maga körül. Gyakran használjuk a lineáris vezető kifejezést. Ez hasonló absztrakció, mint a ponttöltés bevezetése sztatikában. Itt arra kell gondolni, hogy adott egy görbe a térben, és ennek a görbének minden pontjában egy 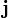 áramsűrűség van, amely párhuzamos a görbe irányvektorával. Az áramot valamilyen potenciálkülönbség hajtja körben az áramkörben. Ezt valamilyen hatással (kémiai, mechanikai, stb.) létre kell hozni, és fenn kell tartani. Erre bevezetjük az elektromotoros erőt: ez azzal a térerősséggel egyenlő, amely a töltésszétválasztás során létrejött teret kompenzálja, ha nem folyik áram.
áramsűrűség van, amely párhuzamos a görbe irányvektorával. Az áramot valamilyen potenciálkülönbség hajtja körben az áramkörben. Ezt valamilyen hatással (kémiai, mechanikai, stb.) létre kell hozni, és fenn kell tartani. Erre bevezetjük az elektromotoros erőt: ez azzal a térerősséggel egyenlő, amely a töltésszétválasztás során létrejött teret kompenzálja, ha nem folyik áram.
Kirchhoff törvények[2]
A Kirchhoff-törvények a villamosságtanban a töltés és az energia megmaradását tárgyalják. Feladatok esetén is jól alkalmazhatjuk (ablak módszer).
- Huroktörvény (energia megmaradás): Egy zárt áramköri hurokban a feszültségek előjeles összege zérus (feltéve, hogy nincs külső mágneses tér).
- Csomópont-törvény (töltésmegmaradás): Az egy áramköri csomópontban összefutó áramok előjeles összege zérus. Ez a kontinuitási egyenlet speciális esete.
Ohm-törvény
Általában: 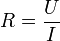
A lokális Ohm-törvény:
ahol 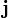 az áramsűrűség,
az áramsűrűség, 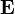 az elektromos térerősség,
az elektromos térerősség, 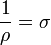 a fajlagos vezetőképesség és
a fajlagos vezetőképesség és 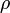 a fajlagos ellenállás. Fontos megjegyezni, hogy ezt sem tartalmazzák a Maxwell-egyenletek, tulajdonképpen ez is anyagi egyenlet. Lásd a kereszteffektusoknál található levezetést.
a fajlagos ellenállás. Fontos megjegyezni, hogy ezt sem tartalmazzák a Maxwell-egyenletek, tulajdonképpen ez is anyagi egyenlet. Lásd a kereszteffektusoknál található levezetést.
Érdemes megyjegyezni, hogy a kontinuitási egyenlet miatt az áramsűrűség normális komponense a határfelületeken egyenlő, azonban ha két olyan anyag van a két oldalon, amelyek vezetőképessége (ellenállása) más, akkor a térerősség is különböző kell, hogy legyen, és az eredmény az, hogy a felületen töltésfelhalmozódás alakul ki.
Mágneses hatások
Az egyenárammal átjárt lineáris vezető egy infinitezinális darabja által létrehozott mágneses teret integrálva a vezető vonalára megkapjuk a mágneses teret. Ezt a Biot-Savart törvény adja meg. Ez levezethető a stacionáruis állapotot leíró Maxwell-egyenletekből:
Az eredmény:
Ennek egy speciális alkalmazása, amit igen sokszor használ a fizika, az egyetlen kis áramhurok által látrehozott mágneses tér. Ha a hurokban I áram folyik, akkor bevezetjük a mágneses momentumot (hasonló az elektromos dipólhoz):
ahol az áramot a hurok által behatárolt felület nagyságával szoroztuk meg, az irányt a jobbkéz szabály adja. Ennek sehítségével a kis hurok mágneses tere:
Az így létrehozott térben a töltésekre természetesen hat a Lorentz-erő. Ennek következménye az is, hogy két párhuzamos lineáris vezető között erőhatás ébred, ha bennük áram folyik. Ennek mértéke:
Ha egy irányba folyik az áram a két vezetőben, akkor vonzzák egymást, ha ellentétesen, akkor taszítják egymást.
Tekercsek
Ha feltekerünk hélixbe egy vezetőt, és áramot folyatunk át rajta, akkor az egyes hurkok mágneses tere összeadódik, továbbá jó közelítéssel a tekercsen belül homogén terünk lesz, ami a szélek felé egyre jobban leromlik. A létrehozott B tér egyenesen arányos az áramerősséggel, és a menetszámmal (n).
Hivatkozások: